Это невероятно полезное приближение. Но правда ведет нас гораздо глубже.
Каждый, кто когда-либо посещал курс физики, на протяжении столетий знал один и тот же миф: любой объект, брошенный, выстреленный или выстреленный в гравитационное поле Земли, прежде чем ударится о землю, выстроится по параболе. Если вы пренебрегаете внешними силами, такими как ветер, сопротивление воздуха или любые другие наземные объекты, эта параболическая форма описывает, как центр масс вашего объекта перемещается очень точно, независимо от того, что это такое или что еще задействовано.
Но по законам гравитации парабола - это невозможная форма для объекта, гравитационно связанного с Землей. Математика просто не работает. Если бы мы могли разработать достаточно точный эксперимент, мы бы измерили, что снаряды на Земле делают крошечные отклонения от предсказанной нами параболической траектории, которую мы все вывели в классе: микроскопические в масштабе человека, но все же значительные. Вместо этого объекты, брошенные на Землю, описывают эллиптическую орбиту, похожую на лунную. Вот неожиданная причина.
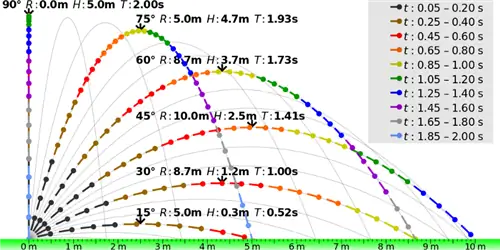
Если вы хотите смоделировать гравитационное поле на поверхности Земли, вы можете сделать два упрощающих предположения:
- Земля, по крайней мере, рядом с вами, плоская, а не изогнутая,
- и гравитационное поле Земли направлено строго вниз относительно вашего текущего местоположения.
Каждый раз, когда вы бросаете и отпускаете объект, он попадает в ситуацию, известную как свободное падение. В направлениях, параллельных поверхности Земли (горизонтальных), скорость любого снаряда останется постоянной. Однако в направлениях, перпендикулярных поверхности Земли (по вертикали), ваш снаряд будет двигаться вниз со скоростью 9,8 м/с²: ускорение под действием силы тяжести на поверхности Земли. Если вы сделаете эти предположения, то вычисляемая вами траектория всегда будет параболой, как раз то, чему нас учат на уроках физики по всему миру.
Но ни одно из этих предположений не верно. Земля может казаться плоской - настолько неотличимой от плоской, что мы не можем обнаружить ее на расстоянии, которое преодолевает большинство снарядов - , но реальность такова, что она имеет сфероидальную форму. Даже на расстоянии всего в несколько метров разница между идеально плоской Землей и изогнутой Землей проявляется на уровне 1-част-в-1 000 000.
Это приближение не так важно для траектории отдельного снаряда, как второе приближение. Из любого места на своем пути снаряд на самом деле не ускоряется «прямо вниз» в вертикальном направлении, а движется к центру Земли. На том же расстоянии в несколько метров разница в углах между «прямо вниз» и «к центру Земли» также играет роль на уровне 1-в-1, 000, 000, но это делает разница.
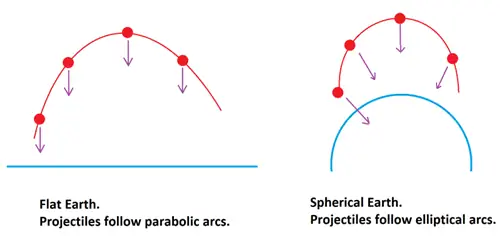
Для типичной системы, такой как футбольный мяч, брошенный ногой, брошенный мяч или даже хоумран в бейсболе, отклонения от параболы будут проявляться на уровне от десятков до, возможно, сотен микрон: меньше одного парамеция. Но истинная траектория завораживает, и она была выведена Иоганном Кеплером более чем за полвека до появления Ньютона.
Как и Луна, любой снаряд следует по эллиптической орбите с центром Земли в качестве одного из фокусов этого эллипса. Единственная трудность для снаряда на Земле, в отличие от Луны, состоит в том, что на пути оказывается сама Земля. В результате мы видим только один крошечный участок эллипса: часть, которая немного возвышается над поверхностью Земли, достигает вершины своей траектории (известной в небесной механике как афелий), а затем падает обратно к центру Земли.
Как только поверхность Земли становится на пути, проблема снова сбрасывается. Если снаряд вообще отскочит, он создаст совершенно новый фрагмент-эллипса, по которому будет следовать его траектория, которая снова может быть очень хорошо аппроксимирована параболой.
Это происходит по простой причине, которую мы обычно считаем само собой разумеющейся: Земля сделана из того же типа материала, обычной материи, из которой сделан типичный снаряд. Обычная материя, которая обычно состоит из протонов, нейтронов и электронов, испытывает не только силу гравитации, но также ядерные и электромагнитные силы. Это электромагнитная сила, которая вызывает типичные взаимодействия, которые мы наблюдаем между частицами, обеспечивая упругие и неупругие столкновения и предотвращая простое проскальзывание наших снарядов через Землю.
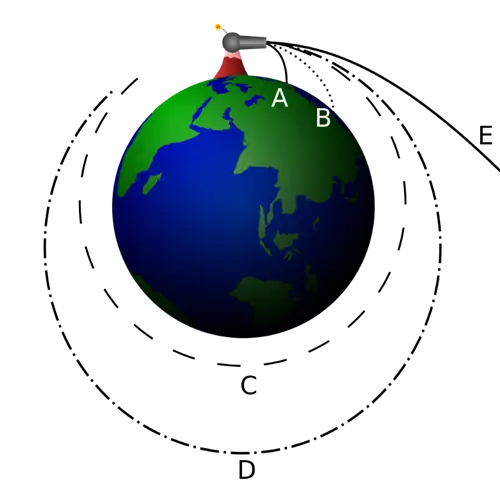
Мы можем обойти эту проблему, представив, что у нас есть что-то, что не взаимодействует с обычной материей в качестве нашего снаряда. Возможно, это может быть нейтрино низкой энергии; возможно, это мог быть сгусток темной материи. В любом случае, этот снаряд, как только мы его выпустим, будет испытывать только гравитационную силу и пройдет через поверхность и внутреннюю часть Земли только под действием гравитационной силы.
Если вы ожидаете, что эта частица сделает замкнутый эллипс и вернется в исходное положение примерно через 90 минут над поверхностью Земли, откуда она была впервые брошена, вы Мы пошли и сделали еще одно приближение, которое не совсем верно. Когда мы рассчитываем орбитальные траектории, мы рассматриваем Землю как единую точку: вся ее масса находится прямо в ее центре. Когда мы рассчитываем траектории спутников, космических станций и даже Луны, это прекрасно работает. Но для частицы, которая проходит через поверхность Земли, такое приближение уже не годится.
Пока вы находитесь вне массы, имеющей форму сферы (или сфероида), вся эта масса гравитационно притягивает вас к центру объекта. Но если вы находитесь только за пределами этой массы (и только ее часть ближе к центру мира, чем вы), то все части этой массы, которые находятся за пределами вашего текущего местоположения, компенсируются.
Вы можете ощутить гравитационный эффект массы, находящейся внутри вас, только если предположить, что все внешние по отношению к вашему положению сферически симметричны. В электромагнетизме это следствие закона Гаусса; в физике гравитации это следствие (родственной) теоремы Биркгофа. Но на практике это означает, что как только вы начинаете падать сквозь Землю, вы испытываете все меньше и меньше гравитационного притяжения внутренней массы.
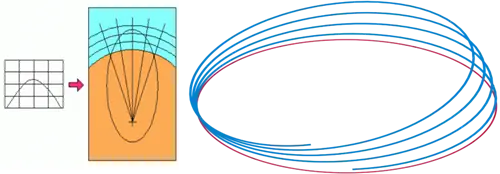
Вместо эллипса, поэтому ваша траектория будет медленно изменяться в более овальную, яйцевидную форму. Когда вы проходили через менее плотную кору и мантию и направлялись к внутреннему и внешнему ядрам, вы замечали не только плавные изменения, но и несколько прерывистых «изгибов» в начертанной вами форме, соответствующих различным слои (разной плотности) в недрах Земли.
Вы бы никогда не появились вновь с другой стороны Земли, но провалились бы мимо центра на некоторое расстояние, разворачиваясь в ядре или мантии в зависимости от каких-то тонких эффектов, которые не т так легко вычислить. Мало того, что различные плотности на разных глубинах не полностью известны, но и скорости вращения различных слоев внутри Земли имеют некоторую неопределенность. Если вы рассматриваете даже единичную массу, проходящую через Землю, в зависимости от точного пути, по которому она движется, динамическое трение также начинает играть роль.
Когда частица проходит мимо других массивных частиц, она гравитационно притягивает их. Если частица пролетит мимо всех остальных частиц, она отклонит их траектории в сторону того места, где она только что прошла, что в конечном итоге приведет к замедлению движения исходной частицы. В зависимости от того, как исходный снаряд был ориентирован относительно вращения Земли и внутренних движений, это может повлиять на траекторию любой частицы, проходящей через Землю.
В течение одного витка, который по-прежнему занимает примерно 85-90 минут или около того, это может иметь достаточно большой эффект, чтобы снаряд не возвращался в исходную начальную точку. Если мы объединим эффекты:
- притяжение эллиптической орбиты из-за точечной массы,
- Теорема Биркгофа для распределенных по пространству масс,
- различная плотность, состав и (возможно) скорость вращения слоев Земли,
- и сложите эффекты динамического трения,
снаряд не совершит замкнутый эллипс, а вместо этого вернется в точку, смещенную от начальной точки на расстояние до ~10 метров.
Для большинства практических приложений никому не помешает рассматривать снаряды как имеющие параболическую траекторию. Но если вы заботитесь о микронной или большей точности или имеете дело с большой конструкцией (например, подвесным мостом), которая простирается на 100 и более метров, вы не можете рассматривать гравитационное поле Земли как константу. Все ускоряется не «вниз», а к центру Земли, что позволяет раскрыть истинную траекторию снаряда - эллипс - .
Изучение различных действующих эффектов, как внешних по отношению к Земле, так и внутри нашей планеты, также может научить нас, когда и при каких обстоятельствах важно учитывать эти соображения. Для большинства приложений сопротивление воздуха является гораздо более серьезной проблемой, чем любые эффекты, такие как различные слои недр Земли или динамическое трение, и рассмотрение гравитационного поля Земли как константы полностью оправдано. Но для некоторых задач эти различия имеют значение. Мы вольны делать любые приближения, какие захотим, но когда наша точность становится ниже критического порога, нам некого винить, кроме самих себя.
