Как рассчитать шансы: 11 шагов (с картинками)

Математическое понятие шансов связано с понятием вероятности, но отличается от него. Проще говоря, шансы - это способ выражения отношения между количеством благоприятных исходов в данной ситуации и количеством неблагоприятных исходов. Обычно это выражается в виде отношения (например, 1: 3 или 1/3). Расчет шансов играет центральную роль в стратегии многих азартных игр, таких как рулетка, скачки и покер. Независимо от того, являетесь ли вы крупным игроком или просто любопытным новичком, умение рассчитывать шансы может сделать азартные игры более приятным (и прибыльным!) Занятием.

Шаги

Часть 1 из 3: Расчет основных коэффициентов

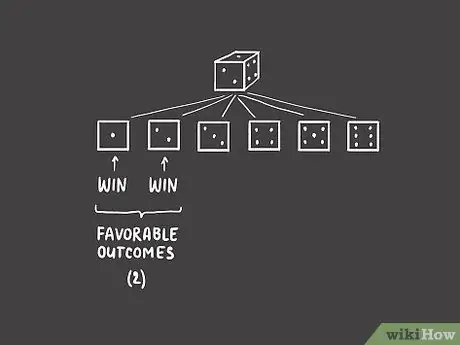
Шаг 1. Определите количество благоприятных исходов в ситуации

Допустим, мы настроены на азартные игры, но все, что нам нужно для игры, - это один простой шестигранный кубик. В этом случае мы просто делаем ставки на то, какое число будет отображаться на кубике после того, как мы его бросим.

Допустим, мы делаем ставку на то, что выбрасываем один или два. В этом случае есть две возможности, при которых мы выигрываем: если на кубике выпадает двойка, мы выигрываем, и если на кубике выпадает единица, мы также выигрываем. Таким образом, есть два благоприятные исходы.

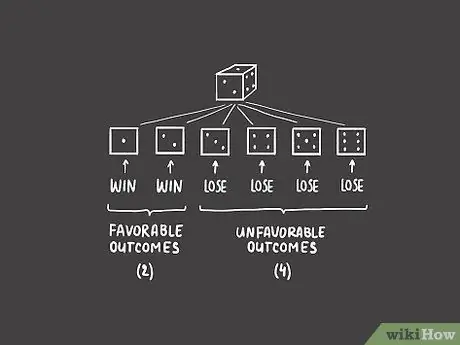
Шаг 2. Определите количество неблагоприятных исходов

В азартной игре всегда есть шанс, что вы не выиграете. Подсчитайте, сколько результатов приведет к проигрышу.

• В примере с кубиком, если мы делаем ставку на то, что выбрасываем один или два, это означает, что мы проиграем, если выпадем три, четыре, пять или шесть. Поскольку есть четыре способа проиграть, это означает, что есть четыре неблагоприятные исходы.
• Другой способ думать об этом - как о Количество общих исходов минус количество благоприятных исходов. При броске кубика существует шесть возможных исходов - по одному на каждое число на кубике. В нашем примере мы бы вычли два (количество желаемых результатов) из шести. 6 - 2 = 4 неблагоприятных исхода.
• Точно так же вы можете вычесть количество неблагоприятных исходов из общего количества исходов, чтобы найти количество благоприятных исходов.

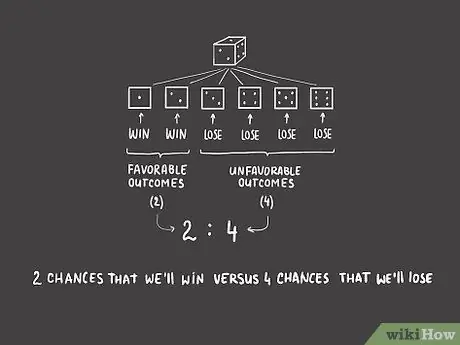
Шаг 3. Выразите шансы численно

Обычно шансы выражаются как соотношение благоприятных исходов к неблагоприятным исходам, часто используют двоеточие. В нашем примере наши шансы на успех будут 2: 4 - два шанса на победу и четыре шанса на поражение. Как дробь, это можно упростить до 1: 2 путем деления обоих членов на общее кратное 2. Это соотношение записывается (прописью) как «один к двум шансам».

Вы можете представить это соотношение в виде дроби. В этом случае наши шансы 2/4, упрощенно как 1/2. Примечание. Коэффициент 1/2 не означает, что у нас есть половина (50%) шансов на победу. Фактически, у нас есть треть шансов на победу. Помните, выражая шансы, что шансы - это отношение благоприятных исходов к неблагоприятным исходам - нет численное измерение вероятности нашей победы.

Шаг 4. Знайте, как рассчитать шансы на то, что событие произойдет

Только что рассчитанные нами шансы 1: 2 - это шансы на нашу победу. Что, если мы хотим знать шансы проиграть, также называемые шансами против нас на победу? Чтобы найти шансы против нас, просто измените соотношение шансов в пользу выигрыша. 1: 2 становится 2: 1.

Если вы выразите шансы на победу дробью, вы получите 2/1. Помните, как и выше, что это не выражение вероятности вашего проигрыша, а скорее отношение неблагоприятных исходов к благоприятным исходам. Если бы это было выражением вашей вероятности проигрыша, у вас был бы шанс проиграть 200%, что, очевидно, невозможно. Как вам такие шансы? На самом деле у вас есть 66% шанс проиграть - 2 шанса проиграть и 1 шанс выиграть означает 2 проигрыша / 3 общих результата = 0,66 = 66%

Шаг 5. Знайте разницу между шансами и вероятностями

Понятия шансов и вероятности связаны, но не идентичны. Вероятность - это просто представление о вероятности того, что данный результат произойдет. Его можно найти путем деления количества желаемых результатов на общее количество возможных результатов. В нашем примере вероятность (не шансы) того, что мы выбросим один или два (из шести возможных результатов броска кубика), равна 2 / 6 = 1 / 3 =.33 = 33%. Таким образом, наши шансы на победу 1: 2 означают, что мы выиграем с вероятностью 33%.

• Легко конвертировать между вероятностью и шансами. Чтобы найти отношение шансов для данной вероятности, сначала выразите вероятность в виде дроби (мы будем использовать 5/13). Вычтем числитель (5) из знаменателя (13): 13 - 5 = 8. Ответ - количество неблагоприятных исходов. Тогда шансы могут быть выражены как 5: 8 - соотношение благоприятных исходов к неблагоприятным.
• Чтобы найти вероятность из заданного отношения шансов, сначала выразите свои шансы в виде дроби (мы будем использовать 9 / 21). Складываем числитель (9) и знаменатель (21): 9 + 21 = 30. Ответ - общее количество исходов. Вероятность можно выразить как 9/30 = 3/10 = 30% - количество благоприятных исходов по отношению к общему количеству возможных исходов.

• Простая формула для расчета шансов по вероятности: О = Р / (1 - Р). Формула для расчета вероятности из шансов: Р = О / (О + 1).

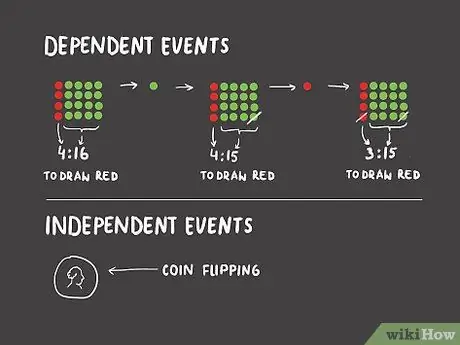
  Часть 2 из 3: Расчет сложных коэффициентов

  

  Шаг 1. Различайте зависимые и независимые события

  В определенных сценариях шансы на данное событие будут меняться в зависимости от результатов прошлых событий. Например, если у вас есть банка, полная двадцати шариков, четыре из которых красные и шестнадцать зеленых, у вас будет шанс 4: 16 (1: 4), чтобы случайно вытащить красный шарик. Допустим, вы нарисовали зеленый шарик. Если вы не положите шарик обратно в банку, при следующей попытке у вас будет шанс 4:15, чтобы вытянуть красный шарик. Затем, если вы вытащите красный шарик, у вас будет шанс 3:15 (1: 5) при следующей попытке. Рисование красного мрамора - это зависимое событие - шансы зависят от того, какие шарики были нарисованы ранее.

  Независимые мероприятия - это события, на шансы которых не влияют предыдущие события. Подбрасывание монеты и выпадение орла - это независимое событие - вероятность того, что вам выпадет орел в прошлый раз, не зависит от того, выпадал орел или решка.

  

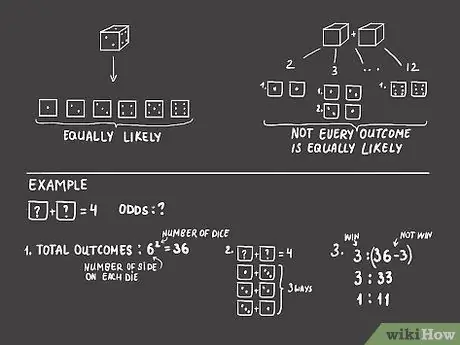
  Шаг 2. Определите, все ли исходы равновероятны

  Если мы бросим один кубик, то с равной вероятностью мы получим любое из чисел от 1 до 6. Однако, если мы бросим два кубика и сложим их числа, хотя есть шанс, что мы получим что-нибудь от 2 до 12, а не все исходы одинаково вероятны. Есть только один способ получить 2 - бросив две единицы - и есть только один способ получить 12 - бросив две шестерки. Напротив, есть много способов сделать семерку. Например, вы можете выбросить 1 и 6, 2 и 5, 3 и 4 и так далее. В этом случае коэффициенты для каждой суммы должны отражать тот факт, что одни исходы более вероятны, чем другие.

  • Давайте сделаем пример задачи. Чтобы рассчитать вероятность выпадения двух кубиков с суммой четырех (например, 1 и 3), начните с вычисления общего количества результатов. У каждой отдельной кости есть шесть результатов. Возьмите количество результатов для каждой кости в степени количества игральных костей: 6 (количество сторон на каждом кубике)^{2 (количество кубиков)} = 36 возможных исходов. Затем найдите количество способов, которыми вы можете сделать четыре с двумя кубиками: вы можете бросить 1 и 3, 2 и 2 или 3 и 1 - три способа. Таким образом, шансы на выпадение комбинированной «четверки» с двумя игральными костями равны 3: (36-3) = 3: 33 = 1: 11
  • Шансы меняются экспоненциально в зависимости от количества событий, происходящих одновременно. Ваши шансы выбросить «яхтзи» (пять кубиков с одним и тем же числом) за один бросок очень малы - 6: 6⁵ - 6 = 6: 7770 = 1: 1295!

  

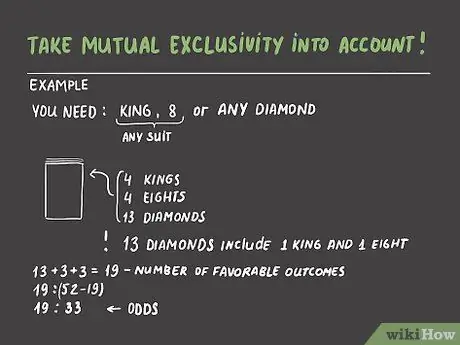
  Шаг 3. Учитывайте взаимную исключительность

  Иногда определенные исходы могут совпадать - рассчитанные вами шансы должны это отражать. Например, если вы играете в покер и у вас на руке бубновая девятка, десятка, валет и дама, вы хотите, чтобы вашей следующей картой был либо король, либо восьмерка любой масти (чтобы получился стрит), либо или любой ромб (чтобы собрать флеш). Допустим, дилер сдает вашу следующую карту из стандартной колоды из пятидесяти двух карт. В колоде тринадцать бубен, четыре короля и четыре восьмерки. Однако общее количество благоприятных исходов не равно 13 + 4 + 4 = 21. Тринадцать бубен уже включают короля и восемь бубен - мы не хотим пересчитывать их дважды. Фактическое количество благоприятных исходов составляет 13 + 3 + 3 = 19. Таким образом, шансы получить карту, которая даст вам стрит или флеш, равны 19: (52 - 19) или 19: 33. Неплохо!

  В реальной жизни, конечно, если у вас уже есть карты в руке, вам редко сдают карты из полной колоды из пятидесяти двух карт. Помните, что количество карт в колоде уменьшается по мере раздачи карт. Кроме того, если вы играете с другими людьми, вам придется угадывать, какие у них карты, когда вы оцениваете свои шансы. Это часть удовольствия от покера

  Часть 3 из 3: Анализ шансов на азартные игры

  

  Шаг 1. Знать распространенные форматы для выражения шансов на азартные игры

  Если вы отправляетесь в мир азартных игр, важно знать, что коэффициенты ставок обычно не отражают истинные математические «шансы» наступления определенного события. Вместо этого ставки на азартные игры, особенно в таких играх, как скачки и ставки на спорт, отражать выплату букмекерской конторы при успешной ставке. Например, если вы ставите 100 долларов на лошадь с коэффициентом 20: 1 против нее, это не означает, что есть 20 исходов, при которых ваша лошадь проигрывает, и 1, при которых она выигрывает. Скорее это означает, что вам заплатят 20 раз ваша первоначальная ставка - в данном случае 2 000 долларов! Что еще больше усугубляет путаницу, формат выражения этих шансов иногда варьируется в зависимости от региона. Вот несколько нестандартных способов выражения шансов на азартные игры:

  • Десятичные (или «европейские») коэффициенты. Их довольно легко понять. Десятичные коэффициенты просто выражаются десятичным числом, например 2.50. Это число представляет собой отношение выплаты к первоначальной ставке. Например, с коэффициентом 2,50, если вы поставите 100 долларов и выиграете, вы получите 250 долларов - в 2,5 раза больше вашей первоначальной ставки. В этом случае вы получите кругленькую прибыль в размере 150 долларов.

  • Дробные (или "британский формат") коэффициенты. Они выражаются в виде дроби, например 1/4.

    Он представляет собой отношение прибыли (а не общей выплаты) от успешной ставки к ставке. Например, если вы поставите 100 долларов на что-то с дробным коэффициентом 1/4 и выиграете, вы получите прибыль в размере 1/4 от первоначальной ставки - в этом случае ваша выплата составит 125 долларов с прибылью в 25 долларов.

  • Коэффициенты на денежную линию (или "американский формат"). Это может быть трудно понять. Коэффициенты денежной линии выражаются числом, которому предшествует знак минус или плюс, например - 200 или +50.

    Знак минус означает, что число представляет, сколько вам нужно поставить, чтобы заработать 100 долларов. Положительный знак означает, что число показывает, сколько вы выиграете, если поставите 100 долларов. Запомните это тонкое различие! Например, если мы поставим 50 долларов с коэффициентом денежной линии -200, когда мы выиграем, мы получим выплату в размере 75 долларов с общей прибылью в 25 долларов. Если мы поставим 50 долларов с коэффициентом денежной линии +200, мы получим выплату в размере 150 долларов с общей прибылью в 100 долларов.

    В коэффициентах денежной линии простая цифра «100» (без плюса или минуса) означает равную ставку - какие бы деньги вы ни поставили, вы получите прибыль в случае выигрыша

  

  Шаг 2. Разберитесь, как устанавливаются шансы на азартные игры

  Коэффициенты, устанавливаемые букмекерскими конторами и казино, обычно не рассчитываются на основе математической вероятности того, что определенные события произойдут. Скорее, они тщательно настроены так, чтобы в долгосрочной перспективе букмекер или казино заработали деньги, независимо от каких-либо краткосрочных результатов! Учитывайте это, делая ставки - помните, что в конце концов казино всегда выигрывает.

  Давайте посмотрим на пример. Стандартное колесо рулетки имеет 38 номеров - от 1 до 36, плюс 0 и 00.. Если вы сделаете ставку на одно место (скажем, 11), у вас есть шансы на победу 1: 37. Однако казино устанавливает коэффициент выплаты 35: 1 - если мяч упадет на 11, вы выиграете в 35 раз больше своей первоначальной ставки. Обратите внимание, что шансы на выплату немного ниже, чем шансы против вашего выигрыша. Если бы казино не интересовались зарабатыванием денег, вам бы выплатили с коэффициентом 37: 1. Однако, устанавливая коэффициенты выплаты немного ниже фактических шансов на ваш выигрыш, казино постепенно будет зарабатывать деньги с течением времени, даже если ему придется время от времени делать крупные выплаты, когда шарик приземляется на 11.

  

  Шаг 3. Не становитесь жертвой распространенных заблуждений, связанных с азартными играми

  Азартные игры могут быть интересными и даже вызывать привыкание. Однако некоторые широко распространенные стратегии азартных игр, которые на первый взгляд кажутся «здравым смыслом», на самом деле математически неверны. Ниже приведены лишь несколько вещей, о которых следует помнить, когда вы играете в азартные игры - не теряйте больше денег, чем необходимо!

  • Вы никогда не должны выиграть. Если вы сидите за столом Техасского Холдема в течение часа и вам не раздали ни одной хорошей руки, вы можете остаться в игре в надежде, что выигрышный стрит или флеш «не за горами».. " К сожалению, ваши шансы не меняются в зависимости от того, сколько времени вы играете в азартные игры. Карты тасуются случайным образом перед каждой раздачей, поэтому, если у вас было десять плохих рук подряд, вы с такой же вероятностью получите еще одну плохую руку, как если бы у вас было сто плохих рук подряд. Это распространяется на большинство других азартных игр - рулетку, игровые автоматы и т. Д.
  • Придерживаясь одной конкретной ставки, вы не увеличите свои шансы. Возможно, вы знаете кого-то, у кого «счастливые» номера лото - хотя может быть интересно делать ставки на числа, которые имеют особое личное значение, в случайных азартных играх у вас никогда не будет больше шансов выиграть, делая ставки на одно и то же каждый раз. чем вы, делая ставку каждый раз на что-то другое. Номера лотереи, слоты и колеса рулетки полностью случайны. Например, в рулетке вероятность того, что вы выбрасываете «9» три раза подряд, столь же велика, как и вероятность того, что вы выберете какие-либо конкретные три числа по порядку.
  • Если вы на один шаг от выигрышного номера, вы не были «близки». Если вы выберете номер 41 для лотереи, а выигрышный номер окажется 42, вы можете почувствовать себя подавленным, но поднимите настроение! Вы даже не были близки. Два близких друг к другу числа, например 41 и 42, никак не связаны математически в случайных азартных играх.

  Шпаргалки по вероятности

  

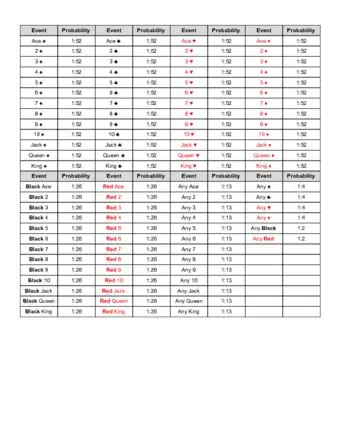
  Таблица вероятностей игральных карт

  Поддержка wikiHow и разблокировать все образцы.

  

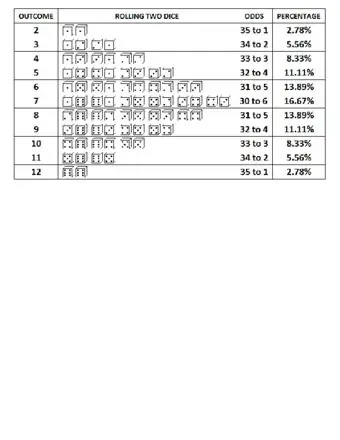
  Примеры вероятностей игры в кости

  Поддержка wikiHow и разблокировать все образцы.

  

  Диаграмма вероятности игры в кости

  Поддержка wikiHow и разблокировать все образцы.

  подсказки

  • Ознакомьтесь с правилами конкретной игры, в которую вы играете, для получения дополнительной информации, которая поможет вам рассчитать шансы.
  • Подсчитать шансы лотереи намного сложнее.
  • Графики, в которых для вас уже рассчитаны шансы, доступны в Интернете.
  • Ищите бесплатные веб-службы ставок в режиме реального времени, которые помогут вам узнать, как производители ставок рассчитывают шансы на предстоящие спортивные события.