4 способа вычисления объема куба

Куб - это трехмерная форма, имеющая одинаковые размеры по ширине, высоте и длине. Куб имеет шесть квадратных граней, каждая из которых имеет стороны равной длины и все пересекаются под прямым углом. Найти объем куба совсем несложно - как правило, все, что нужно, - это умножить объем куба. длина × ширина × высота. Поскольку все стороны куба равны по длине, другой способ представления объема куба - s ³, где s - длина одной из сторон куба. См. Шаг 1 ниже для подробного описания этих процессов.

Шаги

Помощь в определении объема куба

Шпаргалка по объему куба

Поддержка wikiHow и разблокировать все образцы.

Калькулятор объема куба

Поддержка wikiHow и разблокировать все образцы.

Метод 1 из 3: создание одной из сторон куба

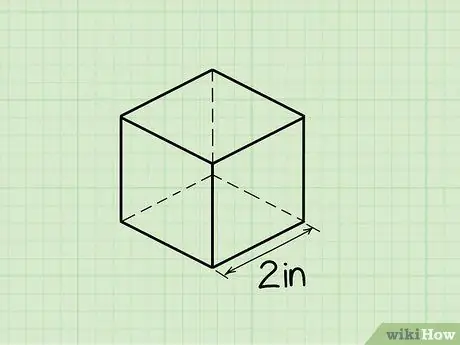
Шаг 1. Найдите длину одной стороны куба

Часто в задачах, просящих вас найти объем куба, вам будет указана длина одной из сторон куба. Если у вас есть эта информация, у вас есть все, что вам нужно для определения объема куба. Если вы не решаете абстрактную математическую задачу, а вместо этого пытаетесь найти объем реального объекта в форме куба, используйте линейку или рулетку, чтобы измерить сторону куба.

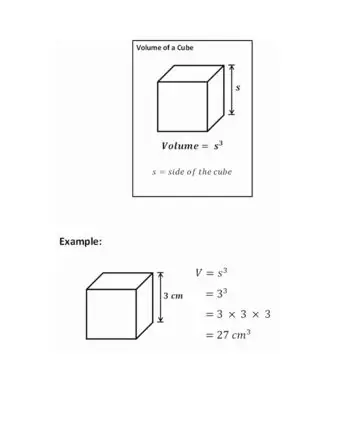
Чтобы лучше понять процесс определения объема куба, давайте рассмотрим пример задачи, выполняя шаги в этом разделе. Допустим, сторона куба 2 дюйма (5,08 см) в длину. Мы будем использовать эту информацию, чтобы найти объем куба на следующем шаге.

Шаг 2. Нарежьте кубиком длину стороны

Когда вы найдете длину одной из сторон куба, возьмите это число в куб. Другими словами, умножьте его на себя дважды. Если s - длина стороны, вы должны умножить s × s × s (или, в упрощенном виде, s ³). Это даст вам объем вашего куба!

• Этот процесс по сути такой же, как нахождение площади основания и последующее умножение ее на высоту куба (или, другими словами, длина × ширина × высота), поскольку площадь основания определяется путем умножения его длины и ширины.. Поскольку длина, ширина и высота куба равны, мы можем сократить этот процесс, просто построив кубик любого из этих измерений.

• Приступим к нашему примеру. Поскольку длина стороны нашего куба составляет 2 дюйма, мы можем найти объем, умножив 2 x 2 x 2 (или 2³) =

  Шаг 8..

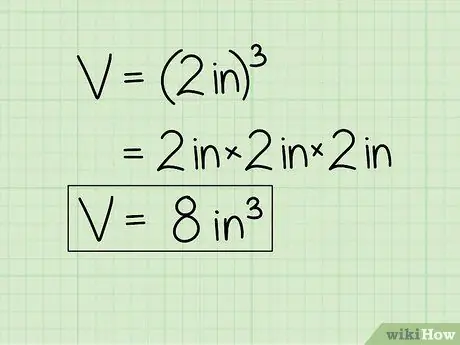
Шаг 3. Обозначьте свой ответ кубическими единицами

Поскольку объем - это мера трехмерного пространства, ваш ответ по определению должен быть в кубических единицах. Часто при выполнении школьных заданий по математике пренебрежение обозначением ответа правильными единицами может привести к потере баллов за задачу, поэтому не забывайте использовать правильный ярлык!

• В нашем примере, поскольку наши исходные измерения были в дюймах, наш окончательный ответ будет обозначен единицами измерения «кубические дюймы» (или в³). Итак, наш ответ 8 становится 8 дюйм³.
• Если бы мы использовали другую начальную единицу измерения, наши конечные кубические единицы были бы другими. Например, если бы у нашего куба были стороны длиной 2 метра, а не 2 дюйма, мы бы пометили его кубические метры (м³).

Метод 2 из 3: определение объема по площади поверхности

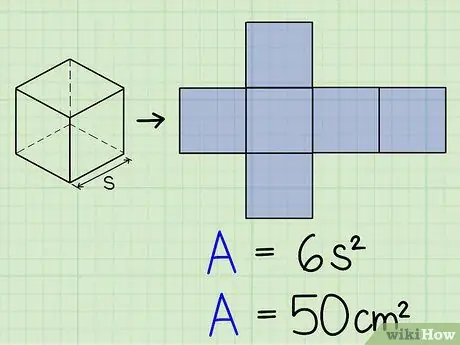
Шаг 1. Найдите площадь поверхности вашего куба

Хотя самый простой способ определить объем куба - это кубить длину одной из его сторон, это не единственный способ. Длина стороны куба или площадь одной из его граней может быть получена из нескольких других свойств куба, что означает, что если вы начнете с одной из этих частей информации, вы можете найти объем куба на круговом перекрестке. манера. Например, если вам известна площадь поверхности куба, все, что вам нужно сделать, чтобы найти его объем, - это разделить площадь поверхности на 6, а затем извлечь квадратный корень из этого значения, чтобы найти длину сторон куба. Отсюда все, что вам нужно сделать, это кубить длину стороны, чтобы найти объем как обычно. В этом разделе мы шаг за шагом рассмотрим этот процесс.

• Площадь поверхности куба определяется формулой 6 с ², где s - длина одной из сторон куба. Эта формула по сути аналогична нахождению двумерной области шести граней куба и сложению этих значений. Мы воспользуемся этой формулой, чтобы найти объем куба по площади его поверхности.
• В качестве рабочего примера предположим, что у нас есть куб, поверхность которого, как мы знаем, 50 см², но мы не знаем длины его сторон. В следующих нескольких шагах мы будем использовать эту информацию, чтобы найти объем куба.

Шаг 2. Разделите площадь куба на 6

Поскольку куб имеет 6 граней с равной площадью, разделив площадь поверхности куба на 6, вы получите площадь одной из его граней. Эта площадь равна длине двух его сторон, умноженных (l × w, w × h или h × l).

В нашем примере деление 50/6 = 8,33 см². Не забывайте, что двумерные ответы имеют квадратные единицы (см², в², и так далее).

Шаг 3. Извлеките квадратный корень из этого значения

Поскольку площадь одной из граней куба равна s ² (s × s), извлекая квадратный корень из этого значения, вы найдете длину одной из сторон куба. Как только вы его получите, у вас будет достаточно информации, чтобы вычислить объем куба, как обычно.

В нашем примере √8,33 примерно 2,89 см.

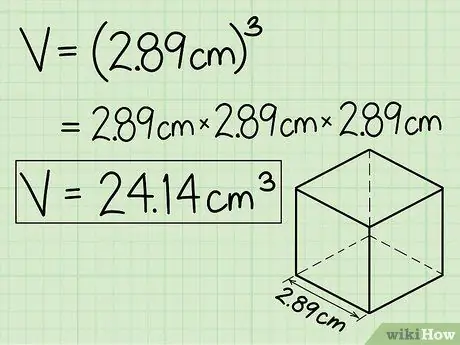
Шаг 4. Возьмите это значение в куб, чтобы найти объем куба

Теперь, когда вы получили значение длины стороны куба, просто возьмите это значение в куб (умножьте его на себя дважды), чтобы найти объем куба, как подробно описано в разделе выше. Поздравляем - вы нашли объем куба по его площади.

В нашем примере 2,89 × 2,89 × 2,89 = 24,14 см³. Не забудьте пометить свой ответ кубическими единицами.

Метод 3 из 3: определение объема по диагоналям

Шаг 1. Разделите диагональ одной из граней куба на √2, чтобы найти длину стороны куба

По определению диагональ полного квадрата равна √2 × длины одной из его сторон. Таким образом, если единственная информация, которую вам дают о кубе, касается длины диагонали одной из его граней, вы можете найти длину стороны куба, разделив это значение на √2. Отсюда относительно просто собрать ответ в куб и найти объем куба, как описано выше.

• Например, предположим, что одна из граней куба имеет диагональ, равную 7 футов длинный. Мы можем найти длину стороны куба, разделив 7 / √2 = 4,96 фута. Теперь, когда мы знаем длину стороны, мы можем найти объем куба, умножив 4,96³ = 122.36 футов³.
• Отметим, что в общих чертах d ² = 2 с ² где d - длина диагонали одной из граней куба, а s - длина одной из сторон куба. Это потому, что согласно теореме Пифагора квадрат гипотенузы прямоугольного треугольника равен сумме квадратов двух других сторон. Таким образом, поскольку диагональ грани куба и две стороны на этой грани образуют прямоугольный треугольник, d ² = s ² + с ² = 2 с ².

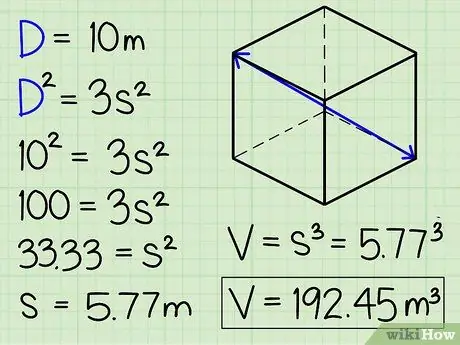
Шаг 2. Возведите диагональ двух противоположных углов куба в квадрат, затем разделите на 3 и извлеките квадратный корень, чтобы найти длину стороны

Если единственная информация, которую вам дают о кубе, - это длина трехмерного линейного сегмента, тянущегося по диагонали от одного угла куба до угла напротив него, все равно можно определить объем куба. Поскольку d образует одну из сторон прямоугольного треугольника с диагональю между двумя противоположными углами куба в качестве гипотенузы, мы можем сказать, что D ² = 3 с ², где D = трехмерная диагональ между противоположными углами куба.

• Это из-за теоремы Пифагора. D, d и s образуют прямоугольный треугольник с D в качестве гипотенузы, поэтому мы можем сказать, что D ² = d ² + с ². Поскольку мы вычислили выше, что d ² = 2 с ², можно сказать, что D ² = 2 с ² + с ² = 3 с ².

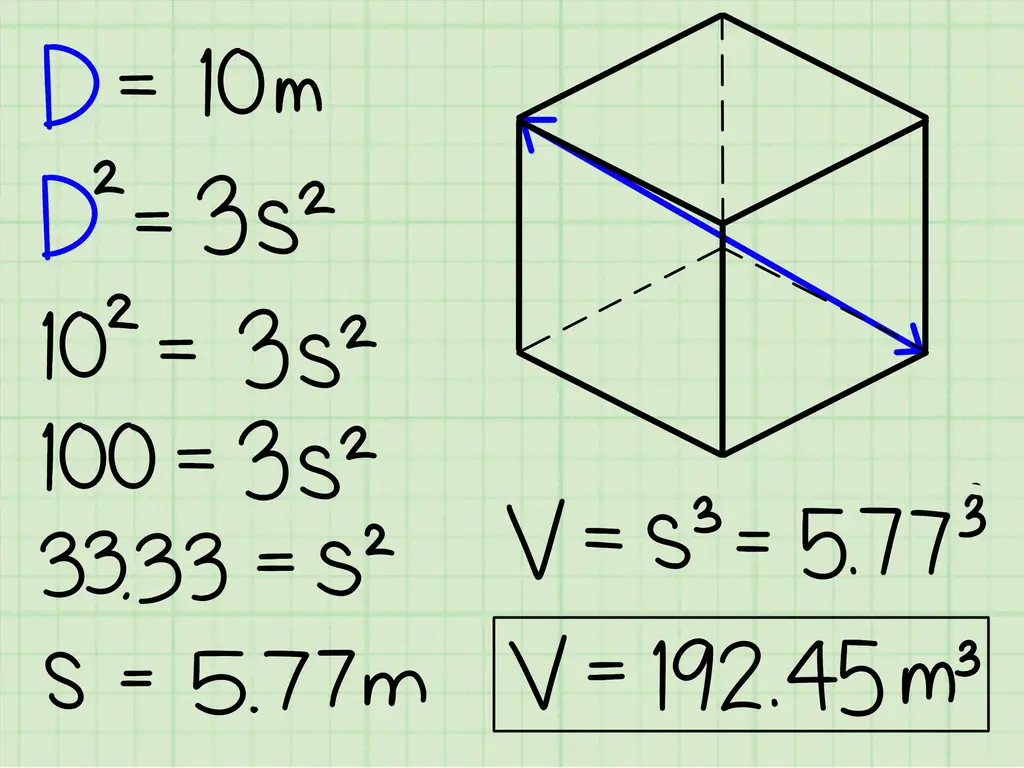
• В качестве примера предположим, что мы знаем, что диагональ от одного из углов в основании куба до противоположного угла в «вершине» куба составляет 10 м. Если мы хотим найти объем, мы должны вставить 10 для каждой буквы «D» в приведенном выше уравнении следующим образом:

  • D ² = 3 с ².
  • 10² = 3 с ².
  • 100 = 3 с ²
  • 33,33 = с ²
  • 5,77 м = s. Отсюда все, что нам нужно сделать, чтобы найти объем куба, - это кубить длину стороны.
  • 5.77³ = 192,45 м³