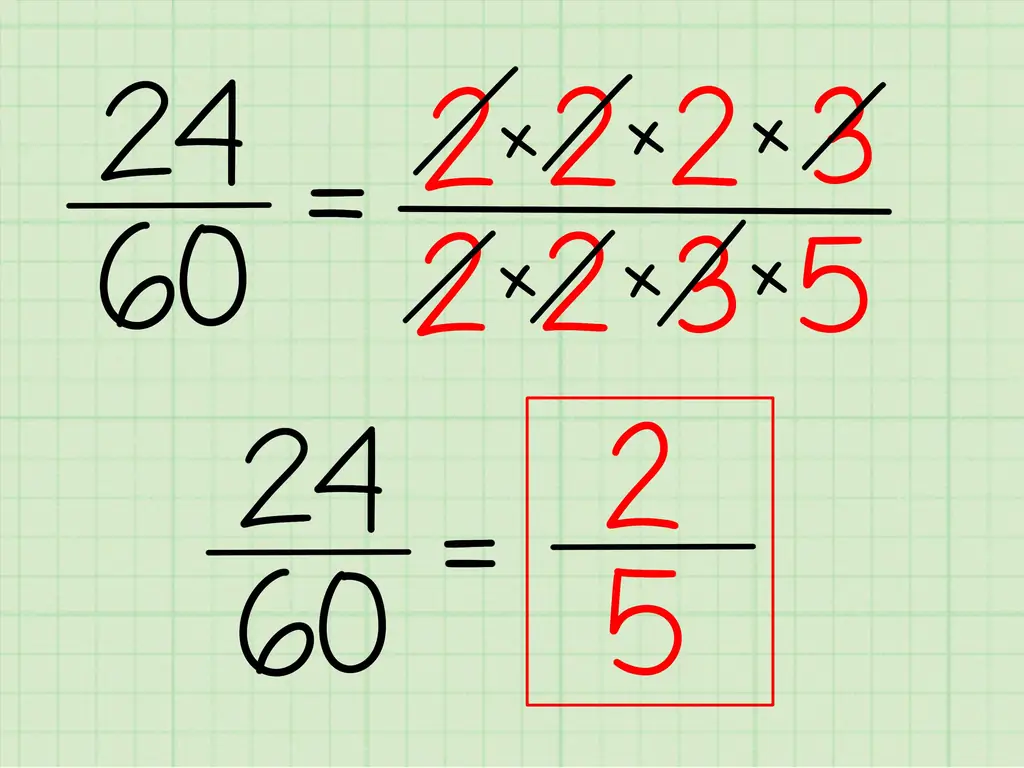Математика - это сложно. Легко забыть даже основные концепции, когда вы пытаетесь запомнить десятки различных принципов и методов. Вот ваш напоминание о двух методах уменьшения дробей.
Шаги
Метод 1 из 4: Использование наибольшего общего множителя

Шаг 1. Составьте список множителей числителя и знаменателя
Факторы - это числа, которые вы умножаете, чтобы получить другое число. Например, 3 и 4 являются множителями 12, потому что вы можете умножить их вместе, чтобы получить 12. Чтобы перечислить множители числа, вам просто нужно перечислить все числа, которые можно умножить, чтобы получить это число, и которые следовательно, можно без остатка разделить на это число.
-
Перечислите множители этого числа от наименьшего к наибольшему, не забывая включать 1 или то же число. Например, вот как вы бы перечислили множители числителя и знаменателя дроби, 24/32:
- 24: 1, 2, 3, 4, 6, 8, 12, 24.
- 32: 1, 2, 4, 8, 16, 32.

Шаг 2. Найдите наибольший общий делитель числителя и знаменателя
GCF - это наибольшее число, которое делится на два или более числа. После того, как вы перечислили все факторы этого числа, все, что вам нужно сделать, это найти наибольшее число, которое повторяется в обоих списках.
-
24: 1, 2, 3, 4, 6,
Шаг 8., 12, 24.
-
32: 1, 2, 4,
Шаг 8., 16, 32.
- GCF 24 и 32 равно 8, потому что 8 - это наибольшее число, которое делится на 24 и 32 без остатка.

Шаг 3. Разделите числитель и знаменатель на GCF
Теперь, когда вы нашли свой GCF, все, что вам нужно сделать, это разделить числитель и знаменатель на это число, чтобы уменьшить вашу дробь до наименьшего значения. Вот как это сделать:
- 24/8 = 3
- 32/8 = 4
- Упрощенная дробь - 3/4.

Шаг 4. Проверьте свою работу
Если вы хотите убедиться, что вы упростили дробь правильно, вы можете просто умножить новый числитель и новый знаменатель на GCF, чтобы убедиться, что вы можете вернуться к исходной дроби. Вот как это сделать:
- 3 * 8 = 24
- 4 * 8 = 32
-
Вы вернулись к исходной дроби, 24/32.
Вы также можете проверить дробь, чтобы убедиться, что ее больше нельзя уменьшить. Поскольку 3 - простое число, оно может делиться только на 1 и само себя, а четыре не делится на 3, поэтому дробь не может быть уменьшена дальше
Метод 2 из 4. Продолжайте делить на небольшое число

Шаг 1. Выберите небольшое количество
Используя этот метод, вам просто нужно выбрать небольшое число, например 2, 3, 4, 5 или 7, чтобы начать работу. Посмотрите на дроби, чтобы убедиться, что каждая из них делится на выбранное вами число хотя бы один раз. Например, если вы смотрите на дробь 24/108, не выбирайте число 5, потому что оно не войдет ни в одно из чисел. Однако, если вы смотрите на дробь 25/60, 5 будет отличным числом для использования.
Для дроби 24/32 хорошо подходит число 2. Поскольку оба числа четные, они делятся на 2

Шаг 2. Разделите числитель и знаменатель дроби на это число
Новая дробь будет состоять из нового числителя и знаменателя, которые вы получите после деления верхней и нижней части дроби 24/32 на 2. Вот как это сделать:
- 24/2 = 12
- 32/2 = 16
- Ваша новая дробь - 12/16.
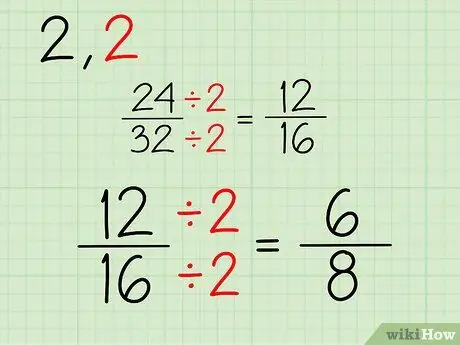
Шаг 3. Повторите
Продолжайте этот процесс. Поскольку оба числа по-прежнему четные, вы можете продолжать делить их на 2. Если только один или оба ваших новых числителя и знаменателя нечетные, вы можете попытаться разделить их на новое число. Вот как будет работать этот процесс, если вы будете придерживаться дроби 12/16:
- 12/2 = 6
- 16/2 = 8
- Ваша новая дробь - 6/8.

Шаг 4. Продолжайте делить на это число, пока не сможете продолжить
И новый числитель, и новый знаменатель по-прежнему четные, поэтому вы можете продолжать делить их на 2. Вот как это сделать:
- 6/2 = 3
- 8/2 = 4
- Ваша новая дробь - 3/4.

Шаг 5. Убедитесь, что дробь не может быть уменьшена дальше
В дроби 3/4 3 является простым числом, поэтому его единственные делители - это 1 и само себя, а 4 не делится на три, поэтому дробь была максимально упрощена. Если числитель или знаменатель дроби больше не может делиться на выбранное вами число, вы все равно можете разделить его, используя новое число.
Например, если у вас есть дробь 10/40 и вы делите числитель и знаменатель на 5, у вас останется 2/8. Вы не можете продолжать делить числитель и знаменатель на 5, но вы можете разделить оба значения на 2, чтобы получить окончательный ответ 1/4

Шаг 6. Проверьте свою работу
Работайте в обратном направлении, чтобы трижды умножить 3/4 на 2/2, чтобы убедиться, что вы получили исходный ответ 24/32. Вот как это сделать:
- 3/4 * 2/2 = 6/8
- 6/8 * 2/2 = 12/16
- 12/16 * 2/2 = 24/32.
- Обратите внимание, что вы разделили 24/32 на 2 * 2 * 2, что равносильно делению на 8, наибольший общий множитель (GCF) 24 и 32.
Метод 3 из 4: перечисление факторов

Шаг 1. Запишите свою дробь
Оставьте большое пространство с правой стороны вашего листа - оно вам понадобится, чтобы записать факторы.

Шаг 2. Составьте список множителей числителя и знаменателя
Храните их в отдельных списках. Может быть проще всего, если списки выстроятся один над другим. Начните с 1 и продвигайтесь вверх, перечисляя их попарно.
-
Например, если ваша дробь 24/60, начните с 24.
Вы бы написали: 24 - 1, 2, 3, 4, 6, 8, 12, 24
-
Затем переходите к 60.
Вы бы написали: 60 - 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60

Шаг 3. Найдите и разделите на наибольший общий делитель
В вашем учебнике это может называться GCF. Какое наибольшее число входит в числитель и знаменатель? Как бы то ни было, разделите на это оба числа.
В нашем примере наибольшее число, которое является множителем обоих чисел, равно 12. Следовательно, мы делим 24 на 12 и 60 на 12, в результате чего получаем 2/5 - нашу уменьшенную дробь
Метод 4 из 4: Использование деревьев простых множителей

Шаг 1. Найдите простые множители числителя и знаменателя
«Простое» число - это число, которое нельзя разделить ни на какое другое число и остаться целым (кроме себя и 1, конечно). 2, 3, 5, 7 и 11 являются примерами простых чисел.
- Начнем с числителя. От 24 переходите к 2 и 12. Поскольку 2 уже является простым числом, вы закончили с этой ветвью! Затем разделите 12 на еще два числа: 2 и 6. 2 - простое число - отлично! Теперь разделите 6 на два числа: 2 и 3. Теперь у вас есть 2, 2, 2 и 3 в качестве простых чисел.
- Переходим к знаменателю. От 60 ответвите свое дерево до 2 и 30. Затем 30 разделится на 2 и 15. Затем разделите 15 на 3 и 5, оба простые числа. Теперь у вас есть простые числа 2, 2, 3 и 5.
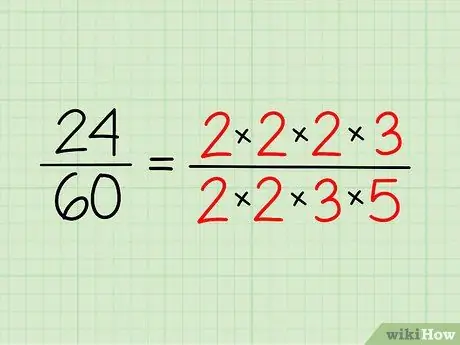
Шаг 2. Напишите факторизацию каждого числа на простые множители
Возьмите список простых чисел, которые у вас есть для каждого числа, и выпишите их для умножения. На самом деле вам не нужно заниматься математикой - это просто упрощает просмотр.
- Итак, для 24 у вас есть 2 x 2 x 2 x 3 = 24.
- Для 60 у вас есть 2 x 2 x 3 x 5 = 60

Шаг 3. Исключите общие факторы
Любые числа, которые вы видите, которые являются частью обоих чисел, можно удалить. В данном случае нас объединяет пара двоек и тройка. До свидания!
- У нас осталось 2 и 5 - или 2/5! Тот же ответ, который мы получили с помощью описанного выше метода.
- если числитель и знаменатель являются четными числами, просто подумайте о том, чтобы разделить число пополам. продолжайте делать это с обоими, пока они не станут слишком маленькими, чтобы их больше нельзя было разделить.