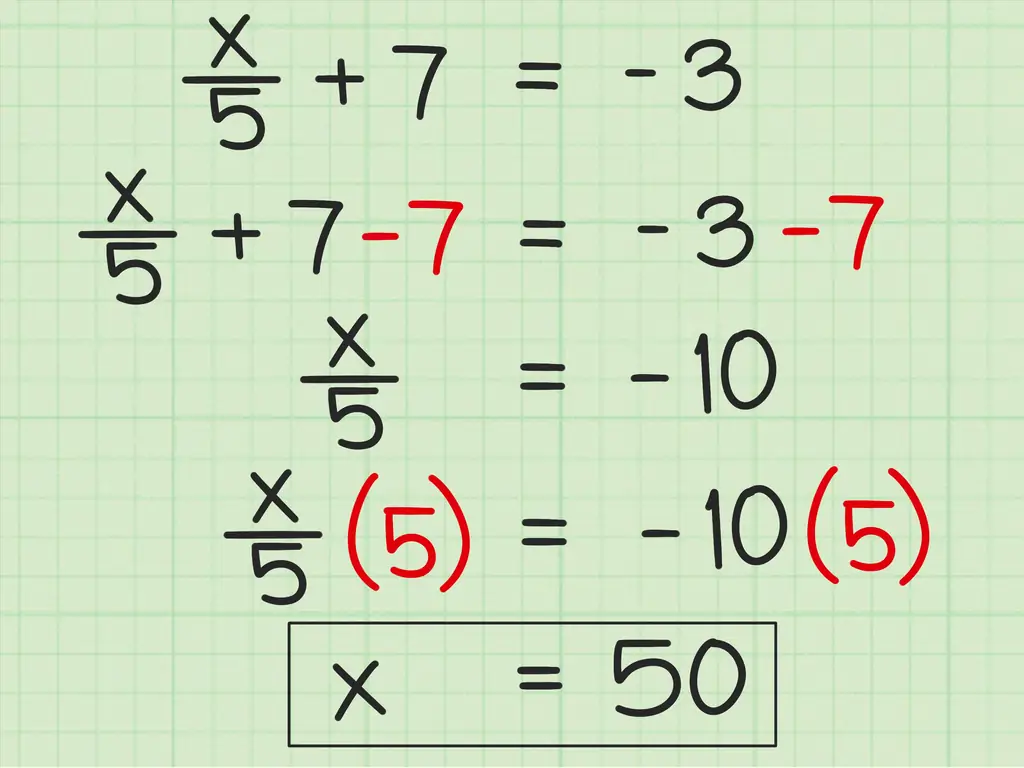Двухшаговые алгебраические уравнения относительно быстрые и легкие - в конце концов, они должны состоять только из двух шагов. Чтобы решить двухшаговое алгебраическое уравнение, все, что вам нужно сделать, это изолировать переменную, используя сложение, вычитание, умножение или деление. Если вы хотите узнать, как решить двухшаговые алгебраические уравнения различными способами, просто выполните следующие действия.
Шаги
Метод 1 из 3: решение уравнений с одной переменной

Шаг 1. Напишите задачу
Первый шаг к решению двухшагового алгебраического уравнения - просто написать задачу, чтобы вы могли начать визуализировать решение. Допустим, мы работаем со следующей проблемой: -4x + 7 = 15.
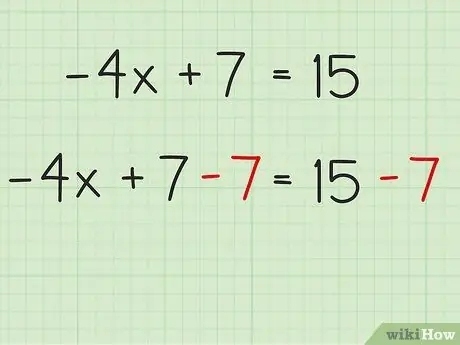
Шаг 2. Решите, использовать ли сложение или вычитание, чтобы выделить переменный член
Следующий шаг - найти способ сохранить «-4x» с одной стороны и сохранить константы (целые числа) с другой стороны. Для этого вам нужно будет выполнить «Аддитивное обратное», найдя противоположность +7, то есть -7. Вычтите 7 из обеих частей уравнения так, чтобы «+7» на той же стороне, что и переменная составляющая, вычеркнулось. Просто напишите «-7» под 7 с одной стороны и под 15 с другой, чтобы уравнение оставалось сбалансированным.
Помните золотое правило алгебры
Все, что вы делаете с одной стороной уравнения, должно быть сделано с другой, чтобы сохранить баланс. Поэтому из 15 также вычитается 7. Нам нужно вычесть 7 только один раз на каждую сторону, поэтому 7 не вычитается также из -4x.

Шаг 3. Добавьте или вычтите константу с обеих сторон уравнения
Это завершит процесс выделения переменного члена. Вычитание 7 из +7 в левой части уравнения не оставит постоянного члена (или 0) в левой части уравнения. Вычитание 7 из +15 в правой части уравнения даст вам 8. Таким образом, новое уравнение будет -4x = 8.
- -4x + 7 = 15 =
- -4x = 8
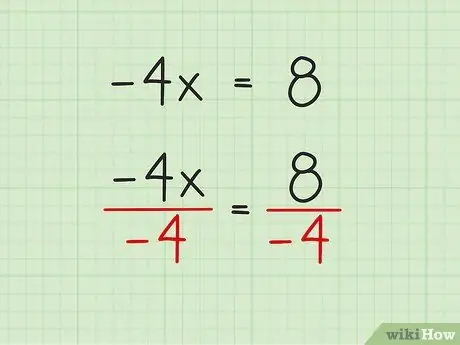
Шаг 4. Исключите коэффициент переменной путем деления или умножения
Коэффициент - это число, прикрепленное к переменной. В этом примере коэффициент равен -4. Чтобы удалить -4 в -4x, вам придется разделить обе части уравнения на -4. Прямо сейчас x умножается на -4, поэтому противоположностью этой операции является деление, и вам придется делать это с обеих сторон.
Опять же, все, что вы делаете с уравнением, должно быть сделано с обеими сторонами. Вот почему вы видите ÷ -4 дважды.

Шаг 5. Найдите переменную
Для этого разделите левую часть уравнения -4x на -4, чтобы получить x. Разделите правую часть уравнения 8 на -4, чтобы получить -2. Следовательно, x = -2. Вы сделали два шага - вычитание и деление - чтобы решить это уравнение.
Метод 2 из 3: решение уравнений с одной переменной с каждой стороны

Шаг 1. Напишите задачу
Проблема, с которой вы будете работать, следующая: -2x - 3 = 4x - 15. Прежде чем продолжить, убедитесь, что обе переменные одинаковы. В этом случае «-2x» и «4x» имеют одну и ту же переменную «x», поэтому вы можете двигаться вперед.

Шаг 2. Переместите константы в правую часть уравнения
Для этого вам нужно использовать сложение или вычитание, чтобы исключить константу из левой части уравнения. Константа равна -3, поэтому вам придется взять ее противоположность, +3, и добавить эту константу к обеим сторонам уравнения.
- Прибавив +3 к левой части уравнения, -2x -3, вы получите (-2x -3) + 3 или -2x в левой части.
- Прибавив +3 к правой части уравнения, 4x -15, вы получите (4x - 15) +3 или 4x -12.
- Следовательно, (-2x - 3) +3 = (4x - 15) +3 = -2x = 4x - 12
- Новое уравнение должно выглядеть так: -2x = 4x -12.

Шаг 3. Переместите переменные в левую часть уравнения
Для этого вам просто нужно взять «противоположное» «4x», то есть «-4x», и вычесть -4x из обеих частей уравнения. С левой стороны -2x - 4x = -6x, а с правой стороны (4x -12) -4x = -12, поэтому новое уравнение должно читать -6x = -12.
2x - 4x = (4x - 12) - 4x = -6x = -12
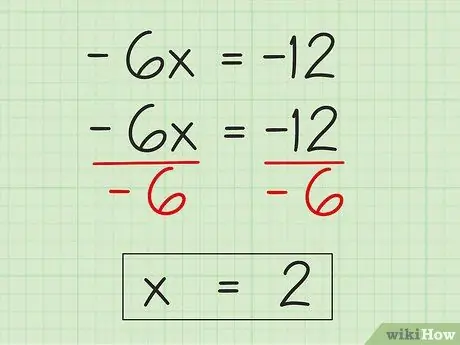
Шаг 4. Найдите переменную
Теперь, когда вы упростили уравнение до -6x = -12, все, что вам нужно сделать, это разделить обе части уравнения на -6, чтобы выделить переменную x, которая в настоящее время умножается на -6. В левой части уравнения -6x ÷ -6 = x, а в правой части уравнения -12 ÷ -6 = 2. Следовательно, x = 2.
- -6x ÷ -6 = -12 ÷ -6
- х = 2
Метод 3 из 3: другие способы решения двухэтапных уравнений

Шаг 1. Решите двухэтапные уравнения, сохраняя переменную справа
Вы можете решить двухэтапное уравнение, сохранив переменную справа. Пока вы изолируете его, вы все равно получите тот же ответ. Возьмем задачу, 11 = 3 - 7x. Чтобы решить эту проблему, первым делом нужно объединить константы путем вычитания 3 из обеих частей уравнения. Затем вам придется разделить обе части уравнения на -7, чтобы найти x. Вот как это сделать:
- 11 = 3 - 7x =
- 11 - 3 = 3 - 3 - 7x =
- 8 = - 7x =
- 8 / -7 = -7 / 7x
- -8/7 = x или -1,14 = x

Шаг 2. Решите двухэтапное уравнение, умножая в конце вместо деления
Принцип решения этого типа уравнения тот же: используйте арифметику, чтобы объединить константы, изолировать член переменной, а затем изолировать переменную без члена. Допустим, вы работаете с уравнением x / 5 + 7 = -3. Первое, что вам нужно сделать, это вычесть 7, обратное к -3, с обеих сторон, а затем умножить обе стороны на 5, чтобы найти x. Вот как это сделать:
- х / 5 + 7 = -3 =
- (x / 5 + 7) - 7 = -3 - 7 =
- х / 5 = -10
- х / 5 * 5 = -10 * 5
- х = - 50
Видео - с помощью этой службы некоторая информация может быть передана YouTube
подсказки
- Внимательно прочтите вопрос.
- При умножении или делении двух чисел с разными знаками (например, одно положительное, а другое отрицательное) результат всегда отрицательный. Если оба знака совпадают, решением будет положительное число.
- Если перед x нет числа, предположим, что это 1x.
- На каждой стороне может не быть явной константы. Если после x нет числа, предположим, что это x + 0.