Как транспонировать матрицу: 11 шагов (с изображениями)

Транспонирование матриц - отличный инструмент для понимания структуры матриц. Возможности, которые вы, возможно, уже знаете о матрицах, такие как прямоугольность и симметрия, очевидным образом влияют на результаты транспонирования. Транспонирование также служит целям при выражении векторов в виде матриц или при получении произведений векторов. Если вы имеете дело со сложными матрицами, тесно связанная концепция сопряженного транспонирования поможет вам решить многие проблемы.

Шаги

Часть 1 из 3: транспонирование матрицы

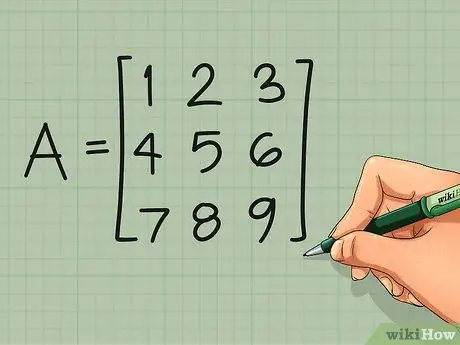
Шаг 1. Начнем с любой матрицы

Вы можете транспонировать любую матрицу, независимо от того, сколько в ней строк и столбцов. Квадратные матрицы с равным количеством строк и столбцов обычно транспонируются, поэтому мы будем использовать простую квадратную матрицу в качестве примера:

• матрица А =

  1 2 3

  4 5 6

  7 8 9

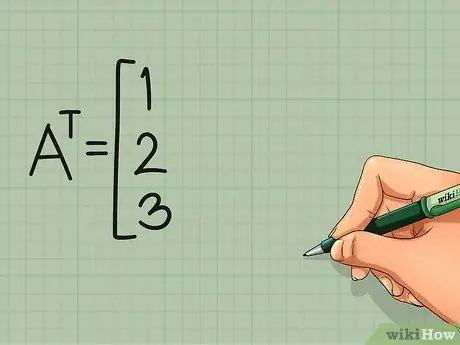
Шаг 2. Превратите первую строку матрицы в первый столбец ее транспонирования

Перепишем первую строку матрицы как столбец:

• транспонировать матрицу A = A^Т

• первый столбец A^Т:

  1

  2

  3

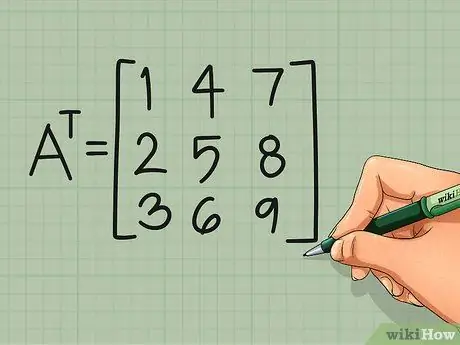
Шаг 3. Повторите для остальных рядов

Вторая строка исходной матрицы становится вторым столбцом ее транспонирования. Повторяйте этот шаблон, пока не превратите каждую строку в столбец:

• А^Т =

  1 4 7

  2 5 8

  3 6 9

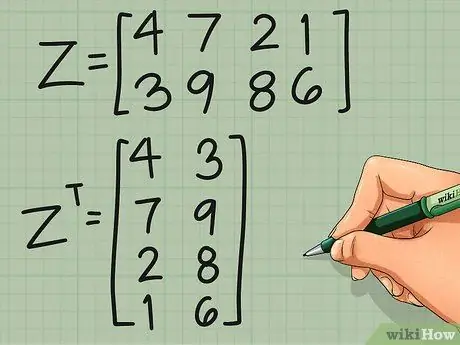
Шаг 4. Практикуйтесь с неквадратной матрицей

Транспонирование точно такое же для неквадратной матрицы. Вы переписываете первую строку как первый столбец, вторую строку как второй столбец и так далее. Вот пример с цветовым кодированием, чтобы показать вам, где заканчиваются элементы:

• матрица Z =

  4 7 2 1

  3 9 8 6

• матрица Z^Т =

  4 3

  7 9

  2 8

  1 6

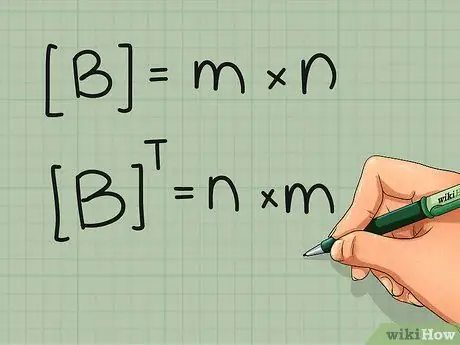
Шаг 5. Выразите транспозицию математически

Идея довольно проста, но хорошо иметь возможность описать ее математически. Никакого жаргона не требуется, кроме основных матричных обозначений:

• Если матрица B является матрицей размером m x n (m строк и n столбцов), транспонированная матрица B^Т представляет собой матрицу размером n x m (n строк и m столбцов).
• Для каждого элемента b _ху (x-я строка, y-й столбец) в B матрица B^Т имеет равный элемент в b _yx (y-я строка, x-й столбец).

Часть 2 из 3: Особые случаи

Шаг 1. (M^{Т) Т = М}.

Транспонирование транспонирования - это исходная матрица. Это довольно интуитивно понятно, поскольку все, что вы делаете, - это переключаете строки и столбцы. Если вы переключите их снова, вы вернетесь с того места, где начали.

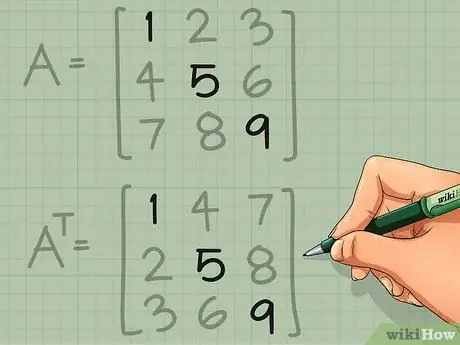
Шаг 2. Переверните квадратные матрицы по главной диагонали

В квадратной матрице транспонирование "переворачивает" матрицу по главной диагонали. Другими словами, элементы по диагонали от элемента a₁₁ в нижний правый угол останется прежним. Элементы друг друга будут перемещаться по диагонали и окажутся на одинаковом расстоянии от диагонали на противоположной стороне.

Если вы не можете это представить себе, нарисуйте матрицу 4х4 на листе бумаги. Теперь складка идет по главной диагонали. Посмотрите, как элементы₁₄ и₄₁ трогать? Они меняются местами в транспонировании, как и друг друга, соприкасающиеся в сложенном состоянии.

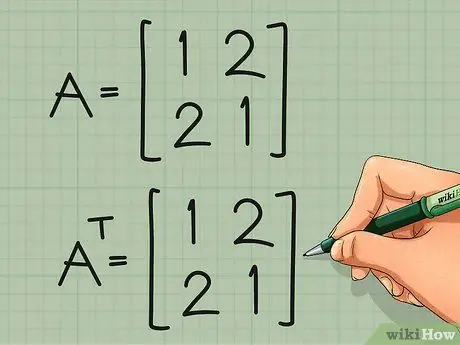
Шаг 3. Транспонируйте симметричную матрицу

Симметричная матрица симметрична по главной диагонали. Если мы воспользуемся приведенным выше описанием «перевернуть» или «свернуть», то сразу увидим, что ничего не меняется. Все пары элементов, которые меняются местами, уже были идентичны. Фактически, это стандартный способ определения симметричной матрицы. Если матрица A = A^Т, то матрица A симметрична.

Часть 3 из 3: Сопряженное транспонирование сложной матрицы

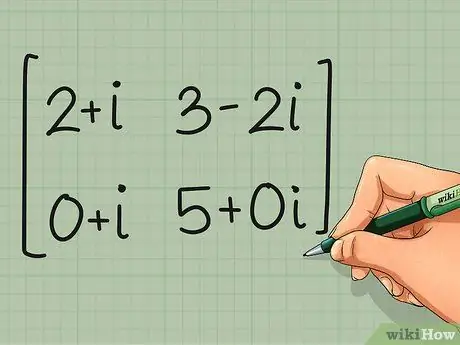
Шаг 1. Начнем со сложной матрицы

Сложные матрицы имеют элементы с действительной и мнимой составляющими. Хотя вы можете использовать обычное транспонирование этих матриц, в большинстве практических вычислений вместо этого используется сопряженное транспонирование.

• Матрица C =

  2+ я 3-2 я

  0+ я 5 + 0 я

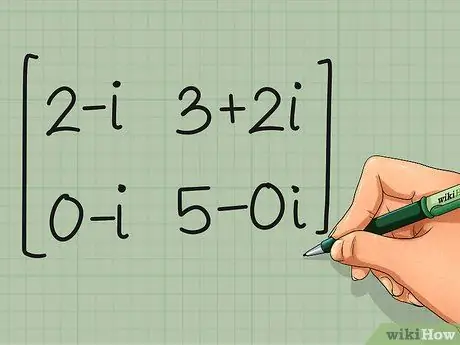
Шаг 2. Возьмите комплексное сопряжение

Комплексное сопряжение меняет знак мнимых компонентов, не изменяя действительные компоненты. Выполните эту операцию для всех элементов матрицы.

• комплексно сопряженный к C =

  2- я 3 + 2 я

  0- я 5-0 я

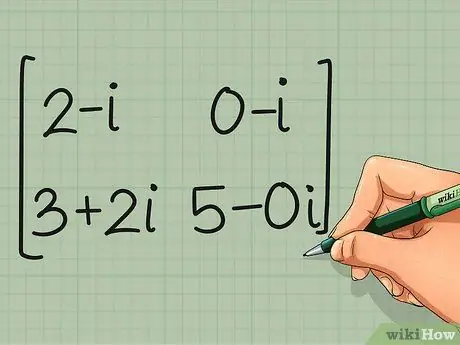
Шаг 3. Переставьте результаты

Возьмем обычную транспозицию результата. Матрица, которую вы получите, является сопряженным транспонированием исходной матрицы.

• сопряженное транспонирование C = C^ЧАС =

  2- я 0- я

  3 + 2 я 5-0 я

Видео - с помощью этой службы некоторая информация может быть передана YouTube

подсказки

• В этой статье используется обозначение A^Т для обозначения транспонирования матрицы A. Обозначения A 'или Ã означают то же самое.
• В этой статье сопряженное транспонирование матрицы A называется A^ЧАС, наиболее распространенные обозначения в линейной алгебре. Квантовые физики часто используют A^† вместо. A * - еще один вариант, но старайтесь избегать его, поскольку некоторые источники будут использовать этот символ для обозначения комплексного сопряжения.