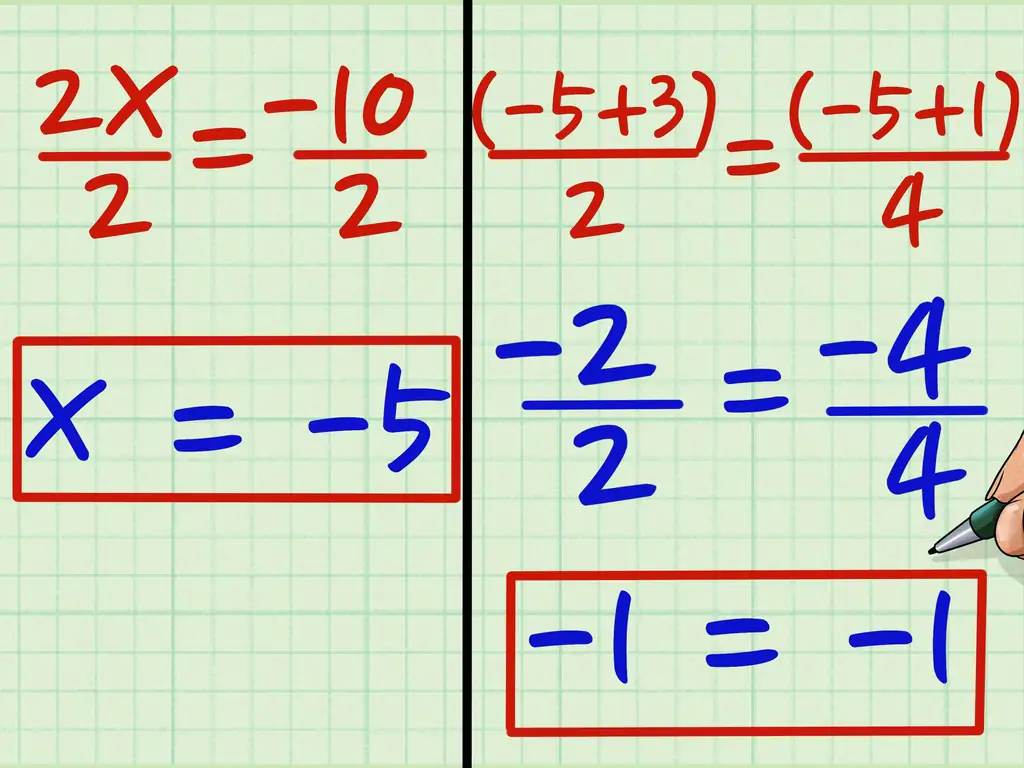Перекрестное умножение - это умный способ решить уравнение, которое включает переменную как часть двух равных друг другу дробей. Переменная является заполнителем для неизвестного числа или количества, а перекрестное умножение сокращает пропорцию до одного простого уравнения, позволяя вам решить для рассматриваемой переменной. Перекрестное умножение особенно полезно, когда вы пытаетесь найти соотношение. Вот как это сделать:
Шаги
Метод 1 из 2: перекрестное умножение с одной переменной
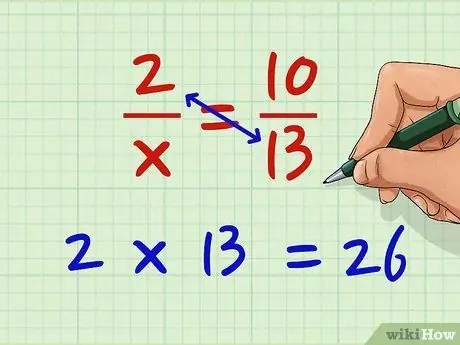
Шаг 1. Умножьте числитель левой дроби на знаменатель правой дроби
Допустим, вы работаете с уравнением 2 / x = 10/13. Теперь умножьте 2 * 13. 2 * 13 = 26.
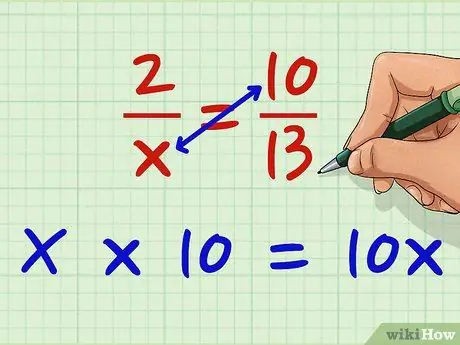
Шаг 2. Умножьте числитель правой дроби на знаменатель левой дроби
Теперь умножьте x на 10. x * 10 = 10x. Вы можете сначала пересечь умножение в этом направлении; на самом деле это не имеет значения, если вы умножаете оба числителя на знаменатели по диагонали от них.
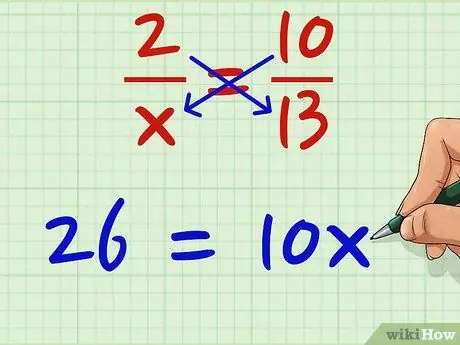
Шаг 3. Установите два продукта равными друг другу
Просто установите 26 равным 10x. 26 = 10х. Неважно, какой номер вы укажете первым; поскольку они равны, вы можете безнаказанно переключать их с одной стороны уравнения на другую, если вы рассматриваете каждый термин как единое целое.
Итак, если вы пытаетесь решить 2 / x = 10/13 относительно x, у вас будет 2 * 13 = x * 10 или 26 = 10x

Шаг 4. Найдите переменную
Теперь, когда вы работаете с 26 = 10x, вы можете начать с поиска общего знаменателя и деления 26 и 10 на число, которое равномерно делится на оба числа. Поскольку они оба четные, их можно разделить на 2; 26/2 = 13 и 10/2 = 5. У вас осталось 13 = 5x. Теперь, чтобы изолировать x, разделите обе части уравнения на 5. Итак, 13/5 = 5x / 5 или 13/5 = x. Если вы хотите получить ответ в десятичной форме, вы можете начать с деления обеих частей уравнения на 10, чтобы получить 26/10 = 10x / 10 или 2,6 = x.
Метод 2 из 2: перекрестное умножение с двумя одинаковыми переменными
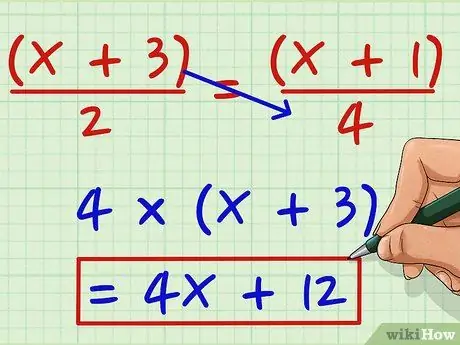
Шаг 1. Умножьте числитель левой дроби на знаменатель правой дроби
Допустим, вы работаете со следующим уравнением: (x + 3) / 2 = (x + 1) / 4. Умножьте (x + 3) на 4, чтобы получить 4 (x +3). Распределите 4, чтобы получить 4x + 12.

Шаг 2. Умножьте числитель правой дроби на знаменатель левой дроби
Повторите процесс с другой стороны. (х +1) х 2 = 2 (х +1). Распределите 2, и вы получите 2x + 2.

Шаг 3. Установите два продукта равными друг другу и объедините одинаковые условия
Теперь у вас будет 4x + 12 = 2x + 2. Объедините члены x и постоянные члены на противоположных сторонах уравнения.
- Итак, объедините 4x и 2x, вычтя 2x с обеих сторон. Вычитание 2x из 2x в правой части даст вам 0. В левой части 4x - 2x = 2x, так что у вас останется 2x.
- Теперь объедините 12 и 2, вычтя 12 из обеих частей уравнения. Вычтите 12 из 12 слева, и у вас будет 0, и вычтите 12 из 2 справа, чтобы получить 2-12 = -10.
- У вас осталось 2x = -10.

Шаг 4. Решаем
Все, что вам нужно сделать, это разделить обе части уравнения на 2. 2x / 2 = -10/2 = x = -5. После перекрестного умножения вы обнаружили, что x = -5. Вы можете вернуться и проверить свою работу, вставив -5 для x, чтобы убедиться, что обе части уравнения равны. Они есть. Если вы подставите -5 обратно в исходное уравнение, вы получите -1 = -1.
Видео - с помощью этой службы некоторая информация может быть передана YouTube
подсказки
- Вы можете проверить свою работу, подставив полученный результат прямо в исходную пропорцию. Если пропорция упрощается до допустимого утверждения, такого как 1 = 1, ваша работа была правильной. Если пропорция упрощается до недопустимого утверждения, например 0 = 1, вы допустили ошибку. Например, замена 2,6 в пропорцию дает 2 / (2,6) = 10/13. Умножьте левую пропорцию на 5/5, и вы получите 10/13 = 10/13, действительное утверждение, которое сокращается до 1 = 1. Итак, 2.6 является правильным.
- Обратите внимание: если вы замените другое число (скажем, 5) в той же пропорции, у вас будет 2/5 = 10/13. Даже если вы снова умножите левое уравнение на 5/5, вы получите 10/25 = 10/13, что явно неверно. Последний случай сигнализирует о том, что вы допустили ошибку в своей технике перекрестного умножения.