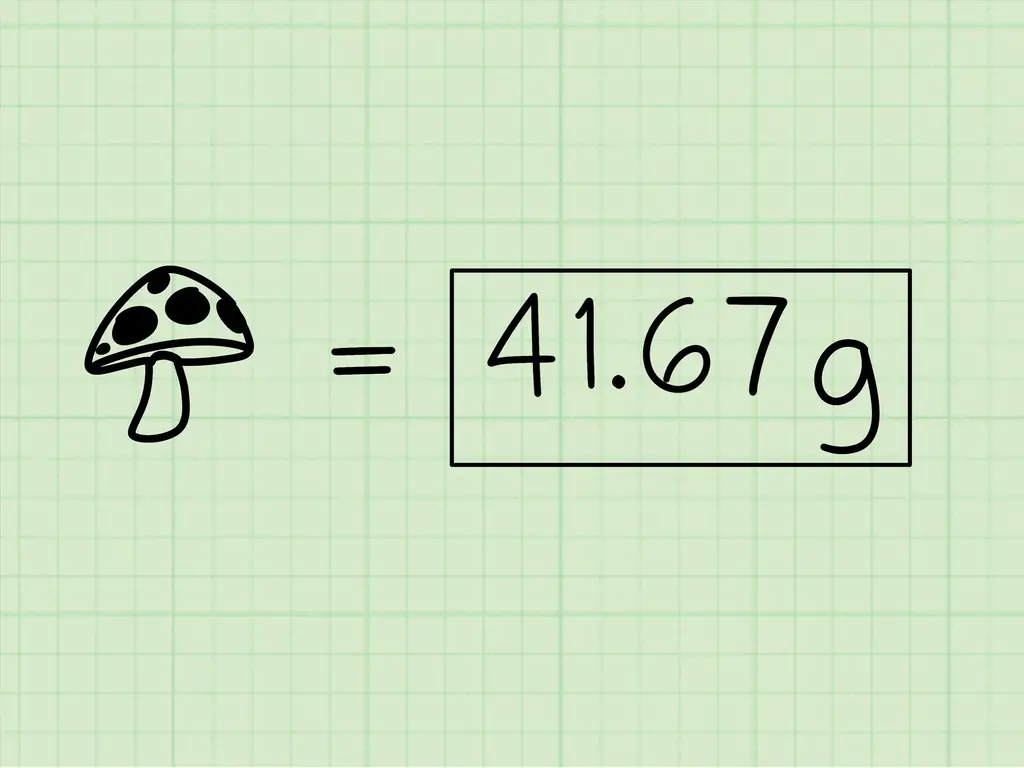Часть основной арифметики, деление в столбик - это метод решения и поиска ответа и остатка для задач деления, которые включают числа, состоящие как минимум из двух цифр. Изучение основных шагов деления в столбик позволит вам делить числа любой длины, включая как целые (положительные, отрицательные и нулевые), так и десятичные дроби. Этому процессу легко научиться, и умение выполнять продольное деление поможет вам отточить математику и лучше понять ее, что будет полезно как в школе, так и в других сферах вашей жизни.
Шаги
Часть 1 из 4: разделение

Шаг 1. Составьте уравнение
На листе бумаги напишите делимое (число деления) справа под символом деления и делимое (число, делающее деление) слева снаружи.
- Частное (ответ) в конечном итоге будет сверху, прямо над дивидендом.
- Оставьте достаточно места под уравнением для выполнения нескольких операций вычитания.
- Вот пример: если в упаковке по 250 грамм шесть грибов, сколько в среднем весит каждый гриб? В этом случае мы должны разделить 250 на 6. 6 идет снаружи, а 250 - внутри.

Шаг 2. Разделите первую цифру
Работайте слева направо и определите, сколько раз делитель может входить в первую цифру делимого, не превышая ее.
В нашем примере вы хотите определить, сколько раз 6 переходит в 2. Поскольку шесть больше двух, ответ равен нулю. Если хотите, можете написать 0 прямо над 2 в качестве заполнителя и стереть его позже. Кроме того, вы можете оставить это поле пустым и перейти к следующему шагу

Шаг 3. Разделите первые две цифры
Если делитель является большим числом, чем первая цифра, определите, сколько раз делитель входит в первые две цифры делимого, не превышая его.
- Если ваш ответ на предыдущем шаге был 0, как в примере, увеличьте число на одну цифру. В этом случае мы бы спросили, сколько раз 6 может перейти в 25.
- Если ваш делитель имеет более двух цифр, вам придется расширить его еще дальше, до третьей или, может быть, даже четвертой цифры делимого, чтобы получить число, в которое входит делитель.
- Работайте в виде целых чисел. Если вы воспользуетесь калькулятором, вы обнаружите, что 6 переходит в 25, всего 4,167 раз. При делении в столбик вы всегда округляете до ближайшего целого числа, поэтому в этом случае наш ответ будет 4.

Шаг 4. Введите первую цифру частного
Укажите, сколько раз делитель переходит в первую цифру (или цифры) делимого над соответствующей цифрой (ами).
- При длинном делении важно следить за тем, чтобы столбцы чисел оставались правильно выровненными. Работайте осторожно, иначе вы можете сделать ошибку, которая приведет к неправильному ответу.
- В этом примере вы поместите 4 над 5, поскольку мы помещаем 6 в 25.
Часть 2 из 4: умножение

Шаг 1. Умножаем делитель
Делитель нужно умножить на число, которое вы только что написали над делимым. В нашем примере это первая цифра частного.

Шаг 2. Запишите продукт
Поместите результат умножения на шаге 1 под делимым.
В этом примере 6 умножить на 4 равно 24. После того, как вы ввели 4 в частном, запишите число 24 под 25, опять же стараясь выровнять числа

Шаг 3. Проведите линию
Линия должна быть помещена под произведением вашего умножения, 24 в этом примере.
Часть 3 из 4: вычитание

Шаг 1. Вычтите произведение
Вычтите число, которое вы только что написали под делимым, из цифр дивиденда непосредственно над ним. Напишите результат под линией, которую вы только что нарисовали.
- В этом примере мы вычтем 24 из 25, получив 1.
- Не вычитайте из полного дивиденда, а только те цифры, с которыми вы работали в первой и второй частях. В этом примере вы не должны вычитать 24 из 250.

Шаг 2. Введите следующую цифру
Запишите следующую цифру делимого после результата операции вычитания.
В этом примере, поскольку 6 не может перейти в 1, не превысив его, вам нужно ввести еще одну цифру. В этом случае вы возьмете 0 из 250 и поместите его после 1, получив 10, в которую может входить 6

Шаг 3. Повторите весь процесс
Разделите новое число на ваш делитель и запишите результат над делимым как следующую цифру частного.
- В этом примере определите, сколько раз 6 может перейти в 10. Запишите это число (1) в частное над делимым. Затем умножьте 6 на 1 и вычтите результат из 10. У вас должно получиться 4.
- Если ваш дивиденд состоит более чем из трех цифр, продолжайте повторять этот процесс, пока вы не проработаете все из них. Например, если бы мы начали с 2 506 граммов (88,4 унций) грибов, мы потянули бы 6 вниз и поместили их рядом с четырьмя.
Часть 4 из 4: остатки и десятичные дроби

Шаг 1. Запишите остаток
В зависимости от того, для чего вы используете это деление, вы можете закончить частным целым числом с остатком, то есть указанием того, сколько осталось после того, как вы завершили свое деление.
- В этом примере остаток будет равен 4, потому что 6 не может перейти в четыре, и нет больше цифр, которые нужно сбрасывать.
- Поместите остаток после частного, поставив перед ним букву «r». В этом примере ответ будет выражен как «41 r4».
- Вы бы остановились здесь, если бы пытались вычислить что-то, что не имеет смысла выражать в частичных единицах, например, если бы вы пытались определить, сколько автомобилей необходимо для перемещения определенного количества людей. В таком случае бесполезно думать о вещах в терминах неполных автомобилей или неполноценных людей.
- Если вы планируете вычислить десятичную дробь, вы можете пропустить этот шаг.

Шаг 2. Добавьте десятичную точку
Если вы планируете вычислить точный ответ, а не ответ с остатком, теперь вам нужно выйти за рамки целых чисел. Когда вы достигли точки, в которой у вас осталось число, меньшее, чем ваш делитель, добавьте десятичную точку как к частному, так и к делимому.
В этом примере, поскольку 250 - это целое число, каждая цифра после десятичной дроби будет равна 0, что составляет 250 000
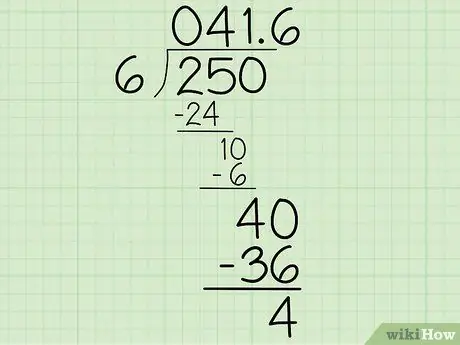
Шаг 3. Продолжайте повторять
Теперь у вас есть больше цифр, которые можно сбить (все они обнуляются). Выведите ноль и продолжайте, как и раньше, определяя, сколько раз делитель может войти в новое число.
В этом примере определите, сколько раз 6 может перейти в 40. Добавьте это число (6) к частному над делимым и после десятичной точки. Затем умножьте 6 на 6 и вычтите результат из 40. Вы должны снова получить 4

Шаг 4. Остановка и круг
В некоторых случаях вы обнаружите, что, когда вы начнете находить десятичную дробь, ответ будет повторяться снова и снова. На этом этапе пора остановиться и округлить ответ в большую сторону (если повторяющееся число 5 или больше) или в меньшую сторону (если 4 или меньше).
- В этом примере вы можете постоянно получать 4 из 40-36 и бесконечно прибавлять 6 к своему частному. Вместо этого остановите проблему и округлите частное. Поскольку 6 больше (или равно) 5, вы округлите до 41,67.
- В качестве альтернативы вы можете указать повторяющуюся десятичную дробь, поместив небольшую горизонтальную линию над повторяющейся цифрой. В этом примере частное составит 41,6 с линией над 6.

Шаг 5. Добавьте единицу к вашему ответу
Если вы работаете с такими единицами измерения, как фунты, галлоны или градусы, после того, как вы закончите все свои вычисления, добавьте единицу измерения в конец вашего ответа.
- Если вы добавили ноль в качестве заполнителя в начале, вам следует стереть и его сейчас.
- В этом примере, поскольку вы спросили, сколько весит каждый гриб в 250-граммовой упаковке из 6 штук, вам нужно будет выразить свой ответ в граммах. Таким образом, ваш окончательный ответ - 41,67 грамма.
Видео - с помощью этой службы некоторая информация может быть передана YouTube
подсказки
- Начните с простых вычислений. Это придаст вам уверенности и разовьет необходимые навыки, чтобы перейти к более продвинутым.
- Ищите практические примеры из повседневной жизни. Это поможет изучить процесс, потому что вы увидите, насколько он полезен в реальном мире.
- Если у вас есть время, рекомендуется сначала провести расчеты на бумаге, а затем проверить с помощью калькулятора или компьютера. Помните, что машины иногда дают неправильные ответы по разным причинам. Если есть ошибка, вы можете провести третью проверку, используя логарифмы. Деление деления вручную, а не использование машин, полезно для ваших математических навыков и концептуального понимания.
- Один из способов запомнить шаги к делению в столбик: «Папа, мама, сестра и брат». D для деления числа, M для умножения, S для вычитания и B для уменьшения цифры.