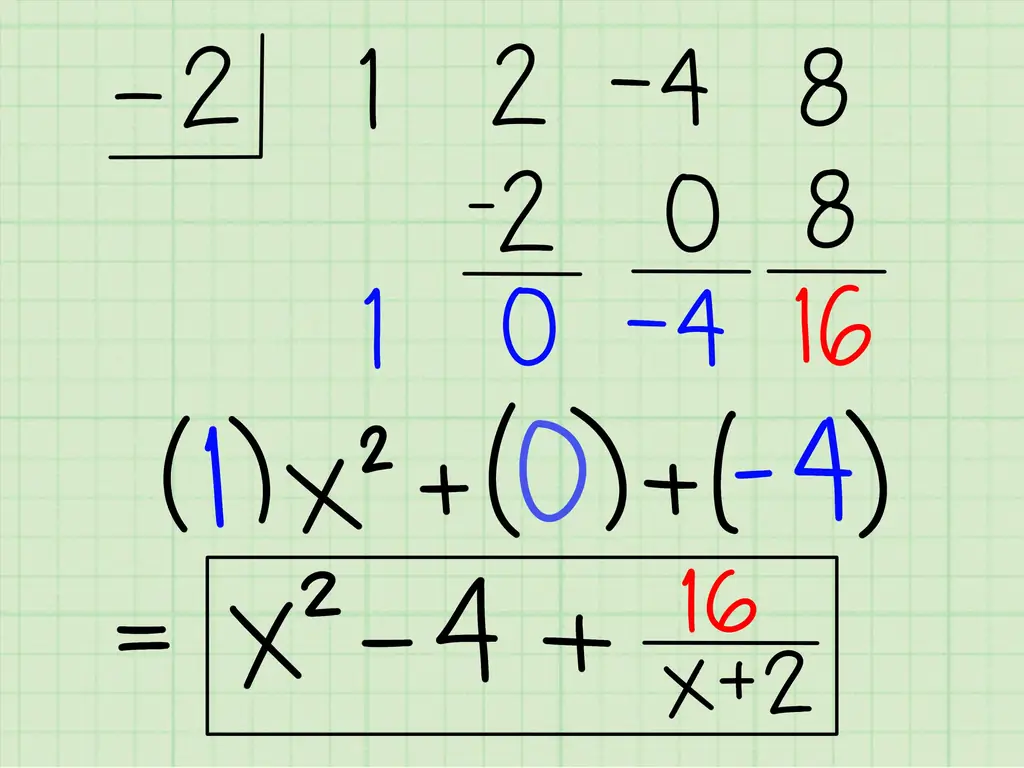Как разделить многочлены с помощью синтетического деления: 12 шагов

Синтетическое деление - это сокращенный метод деления многочленов, при котором вы делите коэффициенты многочленов, удаляя переменные и показатели. Это позволяет вам на протяжении всего процесса складывать, а не вычитать, как при традиционном делении в столбик. Если вы хотите узнать, как делить многочлены с помощью синтетического деления, просто выполните следующие действия.

Шаги

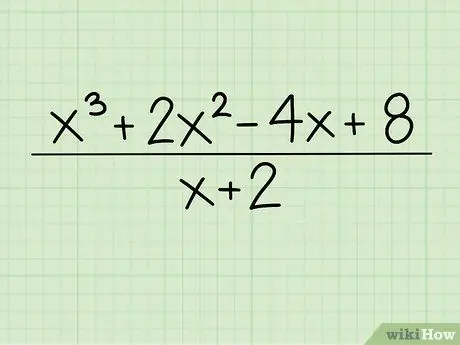
Шаг 1. Запишите проблему

В этом примере вы разделите x³ + 2x² - 4x + 8 на x + 2. Запишите первое полиномиальное уравнение, делимое, в числитель, а второе уравнение, делитель, в знаменатель.

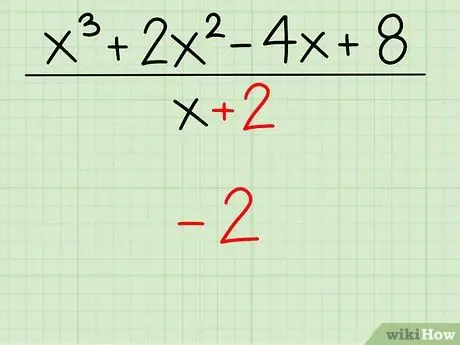
Шаг 2. Поменяйте знак константы в делителе

Константа в делителе x + 2 положительна 2, поэтому изменение знака константы даст вам -2.

Шаг 3. Поскольку постоянный член равен -2, мы помещаем -2 в рамку

Распространенная ошибка - ставить 2 внутри коробки, будьте осторожны.

Шаг 4. Запишите все коэффициенты делимого внутри символа деления

Напишите термины слева направо, как они появляются. Должно получиться так: -2 | 1 2-4 8.

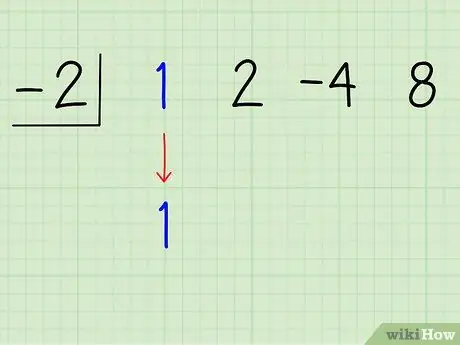
Шаг 5. Сбросьте первый коэффициент

Уменьшите первый коэффициент, 1, ниже самого себя. Должно получиться так:

• -2| 1 2 -4 8

  ↓

  1

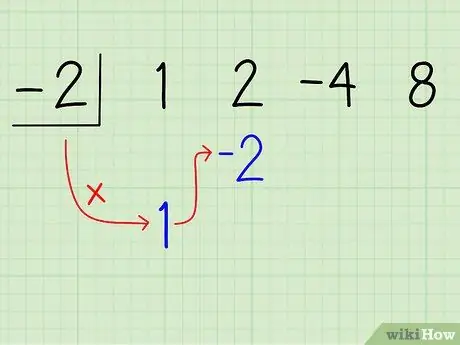
Шаг 6. Умножьте первый коэффициент на делитель и поместите его под вторым коэффициентом

Просто умножьте 1 на -2, чтобы получить -2, и запишите это произведение под вторым членом 2. Вот как это будет выглядеть:

• -2| 1 2 -4 8

  -2

  1

Шаг 7. Сложите второй коэффициент и произведение и напишите ответ под произведением

Теперь возьмите второй коэффициент 2 и прибавьте его к -2. Результатом будет 0. Напишите этот результат под двумя числами, как при делении в столбик. Вот как бы это выглядело:

• -2| 1 2 -4 8

  -2

  1 0

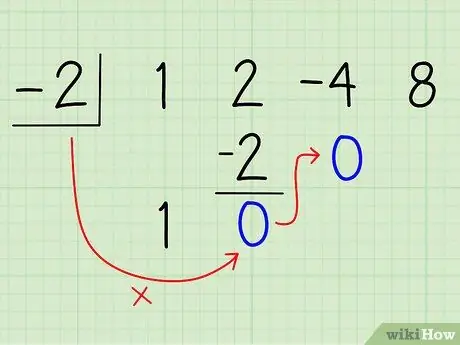
Шаг 8. Умножьте эту сумму на делитель и поместите результат под третий коэффициент

Теперь возьмите сумму 0 и умножьте ее на делитель -2. Результат - 0. Поместите это число под 4, третьим коэффициентом. Должно получиться так:

• -2| 1 2 -4 8

  -2 0

  1

Шаг 9. Сложите произведение и третий коэффициент и запишите результат под произведением

Сложите 0 и -4, чтобы получить -4, и запишите этот ответ под 0. Вот как это будет выглядеть:

• -2| 1 2 -4 8

  -2 0

  1 0 -4

Шаг 10. Умножьте это число на делитель, запишите его под последним коэффициентом и прибавьте к коэффициенту

Теперь умножьте -4 на -2, чтобы получить 8, запишите этот ответ под четвертым коэффициентом, 8, и прибавьте этот ответ к четвертому коэффициенту. 8 + 8 = 16, так что это ваш остаток. Напишите этот номер под продуктом. Вот как бы это выглядело:

• -2| 1 2 -4 8

  -2 0 8

  1 0 -4 |16

Шаг 11. Поместите каждый из новых коэффициентов рядом с переменной, мощность которой на одну меньше, чем их исходные соответствующие переменные

В этом случае первая сумма, 1, ставится рядом с x во второй степени (на единицу меньше трех). Вторая сумма, 0, помещается рядом с x, но результат равен нулю, поэтому вы можете удалить этот член. И третий коэффициент, -4, становится константой, числом без переменной, поскольку исходная переменная была x. Вы можете написать R рядом с 16, потому что это остаток. Вот как бы это выглядело:

• -2| 1 2 -4 8

  -2 0 8

  1 0 -4 |16

  Икс ² + 0 х - 4 р 16

  Икс ² - 4 R16

Шаг 12. Напишите окончательный ответ

Окончательный ответ - новый многочлен x² - 4 плюс остаток 16 по исходному делителю x + 2. Вот как это будет выглядеть: x² - 4 + 16 / (х +2).

Видео - с помощью этой службы некоторая информация может быть передана YouTube

подсказки

• Чтобы проверить свой ответ, умножьте частное на делитель и сложите остаток. Он должен быть таким же, как исходный многочлен.

  (делитель) (частное) + (остаток)

  (х + 2) (х ² - 4) + 16

  Используя метод FOIL, умножьте.

  (Икс ³ - 4 х + 2 х ² - 8) + 16

  Икс ³ + 2 х ² - 4 х - 8 + 16

  Икс ³ + 2 х ² - 4 х + 8