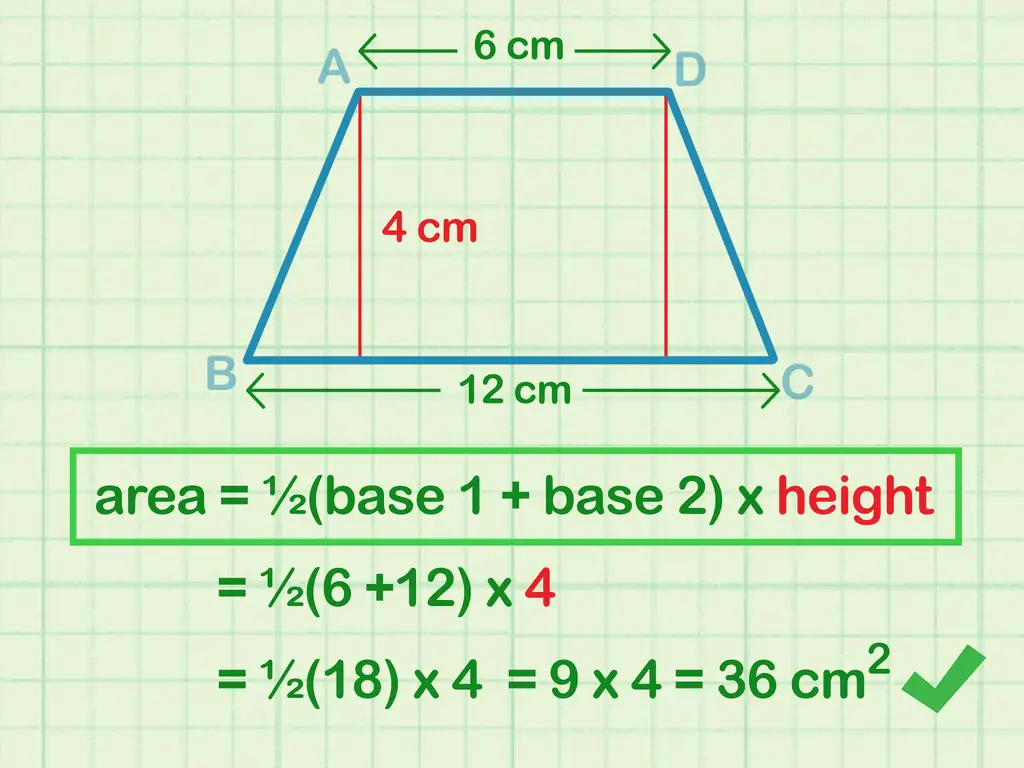
Трапеция, также известная как трапеция, представляет собой 4-стороннюю форму с двумя параллельными основаниями разной длины. Формула площади трапеции: A = ½ (b1+ b2) h, где b1 и б2 - длины оснований, h - высота. Если вам известны только длины сторон обычной трапеции, вы можете разбить трапецию на простые формы, чтобы найти высоту и завершить расчет. Когда вы закончите, просто пометьте свои единицы!
Шаги
Метод 1 из 2: определение площади по высоте и длине основания
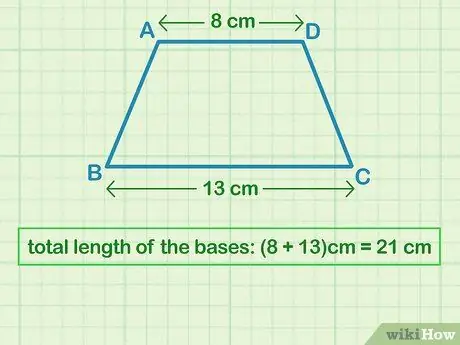
Шаг 1. Сложите длины оснований
Основания - это две параллельные друг другу стороны трапеции. Если вам не даны значения базовой длины, измерьте каждую из них линейкой. Сложите 2 длины вместе, чтобы получить 1 значение.
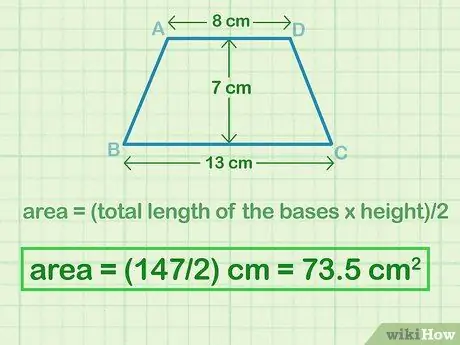
Например, если вы обнаружите, что верхнее основание (b1) составляет 8 см, а нижнее основание (b2) составляет 13 см, общая длина оснований - 21 (8 см + 13 см = 21 см, что отражает "b = b1 + b2"часть уравнения).
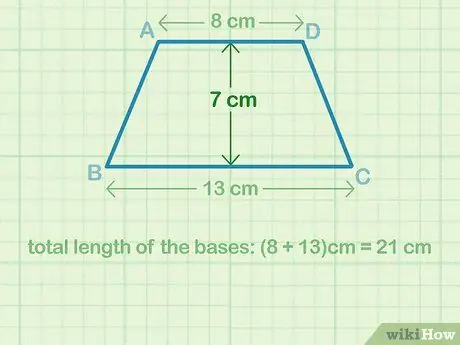
Шаг 2. Измерьте высоту трапеции
Высота трапеции - это расстояние между параллельными основаниями. Проведите линию между основаниями и с помощью линейки или другого измерительного прибора найдите расстояние. Запишите высоту, чтобы не забыть ее позже при расчетах.
Длина скошенных сторон или ножек трапеции не равна высоте. Длина ножки равна высоте только в том случае, если ножка перпендикулярна основанию
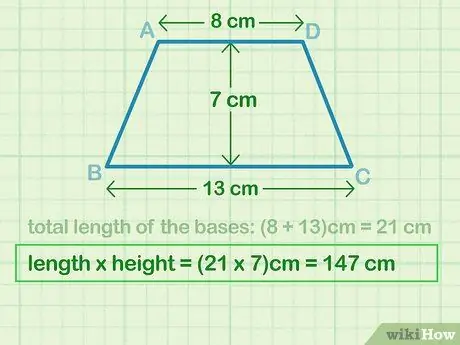
Шаг 3. Умножьте общую длину основания и высоту
Возьмите сумму найденных вами базовых длин (b) и высоты (h) и умножьте их. Напишите продукт в квадратных единицах, соответствующих вашей проблеме.
В этом примере 21 см x 7 см = 147 см.2 который отражает часть уравнения "(b) h".
Шаг 4. Умножьте произведение на ½, чтобы найти площадь трапеции
Вы можете либо умножить произведение на 1/2, либо разделить произведение на 2, чтобы получить конечную площадь трапеции, поскольку результат будет таким же. Обязательно укажите свой окончательный ответ в квадратных единицах.
Для этого примера 147 см.2 / 2 = 73,5 см2, которая является площадью (A).
Метод 2 из 2: Расчет площади трапеции, если вы знаете стороны
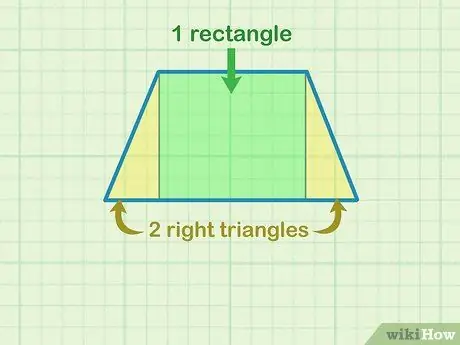
Шаг 1. Разбейте трапецию на 1 прямоугольник и 2 прямоугольных треугольника
Нарисуйте прямые линии вниз от углов верхней основы, чтобы они пересекались и образовывали углы 90 градусов с нижней основой. Внутри трапеции будет 1 прямоугольник посередине и 2 треугольника с каждой стороны одинакового размера и под углом 90 градусов. Рисование фигур помогает лучше визуализировать область и помогает определить высоту трапеции.
Этот метод работает только для обычных трапеций
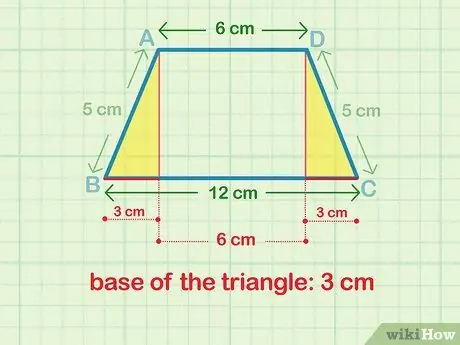
Шаг 2. Найдите длину одного из оснований треугольника
Вычтите длину верхнего основания из длины нижнего, чтобы найти оставшуюся сумму. Разделите полученную сумму на 2, чтобы найти длину основания треугольника. Теперь у вас должна быть длина основания и гипотенуза треугольника.
Например, если верхняя база (b1) составляет 6 см, а нижнее основание (b2) равно 12 см, то основание треугольника равно 3 см (так как b = (b2 - б1) / 2 и (12 см - 6 см) / 2 = 6 см, что может быть упрощено до 6 см / 2 = 3 см).
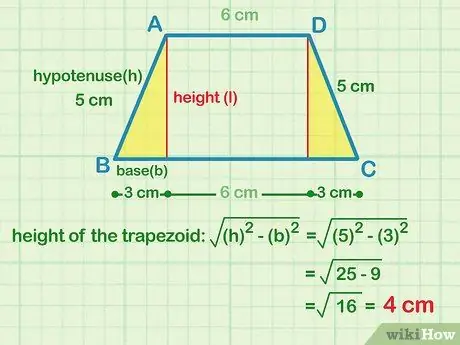
Шаг 3. Используйте теорему Пифагора, чтобы найти высоту трапеции
Подставьте значения длины основания и гипотенузы или самой длинной стороны треугольника в A2 + B2 = C2, где A - основание, C - гипотенуза. Решите уравнение для B, чтобы найти высоту трапеции. Если длина найденного основания 3 см, а длина гипотенузы 5 см, то в этом примере:
- Заполните переменные: (3 см)2 + B2 = (5 см)2
- Упростить квадраты: 9 см + В2 = 25 см
- Отнимите по 9 см с каждой стороны: B2 = 16 см
- Извлеките квадратный корень из каждой стороны: B = 4 см.
Кончик:
Если в вашем уравнении нет полного квадрата, упростите его насколько возможно и оставьте значение квадратным корнем. Например, √32 = √ (16) (2) = 4√2.
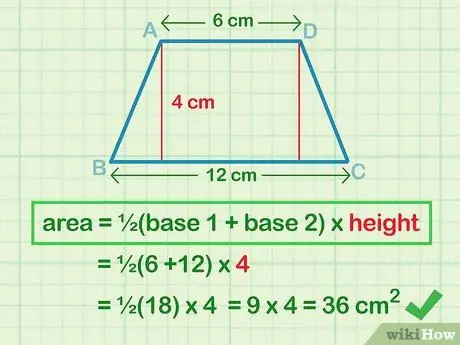
Шаг 4. Вставьте базовую длину и высоту в формулу площади и упростите ее
Положите базовую длину и высоту в формулу A = ½ (b1 + b2) h, чтобы найти площадь трапеции. По возможности упростите число и обозначьте его квадратными единицами.
- Напишите формулу: A = ½ (b1+ b2)час
- Заполните переменные: A = ½ (6 см + 12 см) (4 см)
- Упростите термины: A = ½ (18 см) (4 см)
- Умножаем числа вместе: A = 36 см.2.