Диапазон функции - это набор чисел, которые может произвести функция. Другими словами, это набор значений y, который вы получаете, когда вставляете в функцию все возможные значения x. Этот набор возможных значений x называется доменом. Если вы хотите узнать, как найти диапазон функции, просто выполните следующие действия.
Шаги
Метод 1 из 4: определение диапазона функции по формуле
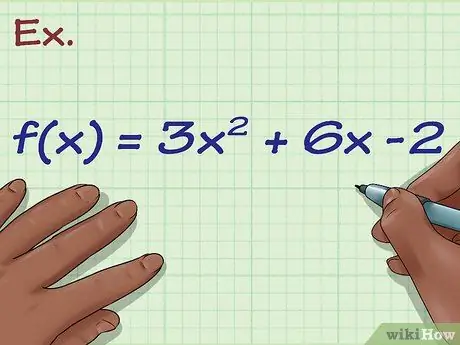
Шаг 1. Запишите формулу
Допустим, вы работаете по следующей формуле: f (x) = 3x2 + 6x -2. Это означает, что когда вы помещаете в уравнение любой x, вы получите значение y. Это функция параболы.

Шаг 2. Найдите вершину функции, если она квадратичная
Если вы работаете с прямой линией или какой-либо функцией с полиномом от нечетного числа, например, f (x) = 6x3+ 2x + 7, этот шаг можно пропустить. Но если вы работаете с параболой или любым уравнением, в котором координата x возведена в квадрат или возведена в четную степень, вам необходимо построить вершину. Для этого просто используйте формулу -b / 2a, чтобы получить координату x функции 3x2 + 6x -2, где 3 = a, 6 = b и -2 = c. В этом случае -b равно -6, а 2a равно 6, поэтому координата x равна -6/6 или -1.
- Теперь вставьте -1 в функцию, чтобы получить координату y. f (-1) = 3 (-1)2 + 6(-1) -2 = 3 - 6 -2 = -5.
- Вершина - (-1, -5). Постройте график, нарисовав точку, где координата x равна -1, а координата y равна -5. Он должен быть в третьем квадранте графика.

Шаг 3. Найдите в функции еще несколько точек
Чтобы получить представление о функции, вы должны подключить несколько других x-координат, чтобы вы могли получить представление о том, как выглядит функция, прежде чем вы начнете искать диапазон. Поскольку это парабола и x2 координата положительна, она будет направлена вверх. Но чтобы охватить ваши базы, давайте подключим некоторые координаты x, чтобы увидеть, какие координаты y они дают:
- f (-2) = 3 (-2)2 + 6 (-2) -2 = -2. Одна точка на графике равна (-2, -2)
- f (0) = 3 (0)2 + 6 (0) -2 = -2. Еще одна точка на графике (0, -2)
- f (1) = 3 (1)2 + 6 (1) -2 = 7. Третья точка на графике - (1, 7).

Шаг 4. Найдите диапазон на графике
Теперь посмотрите на координаты y на графике и найдите самую низкую точку, в которой график касается координаты y. В этом случае самая низкая координата y находится в вершине, -5, и график бесконечно простирается выше этой точки. Это означает, что диапазон функции y = все действительные числа ≥ -5.
Метод 2 из 4: определение диапазона функции на графике

Шаг 1. Найдите минимум функции
Найдите самую низкую координату y функции. Допустим, функция достигает своей нижней точки при -3. Эта функция также может становиться все меньше и меньше бесконечно, так что у нее не будет установленной самой низкой точки - просто бесконечность.
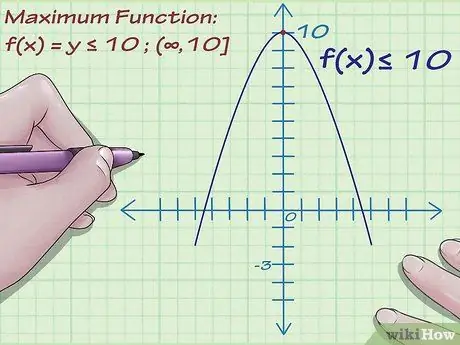
Шаг 2. Найдите максимум функции
Скажем, наивысшая координата Y, которую достигает функция, равна 10. Эта функция также может бесконечно увеличиваться и увеличиваться, поэтому у нее нет установленной наивысшей точки - просто бесконечность.

Шаг 3. Укажите диапазон
Это означает, что диапазон функции или диапазон y-координат находится в диапазоне от -3 до 10. Итак, -3 ≤ f (x) ≤ 10. Это диапазон функции.
- Но предположим, что график достигает самой низкой точки при y = -3, но постоянно идет вверх. Тогда диапазон равен f (x) ≥ -3 и все.
- Скажем, график достигает наивысшей точки в 10, но постоянно идет вниз. Тогда диапазон равен f (x) ≤ 10.
Метод 3 из 4: определение диапазона функции отношения
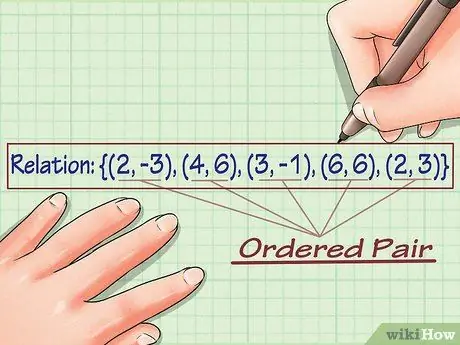
Шаг 1. Запишите отношение
Отношение - это набор упорядоченных пар с координатами x и y. Вы можете посмотреть на отношение и определить его домен и диапазон. Допустим, вы работаете со следующим соотношением: {(2, -3), (4, 6), (3, -1), (6, 6), (2, 3)}.

Шаг 2. Составьте y-координаты отношения
Чтобы найти диапазон отношения, просто запишите все y-координаты каждой упорядоченной пары: {-3, 6, -1, 6, 3}.

Шаг 3. Удалите все повторяющиеся координаты, чтобы у вас была только одна координата каждой y
Вы заметите, что вы указали цифру «6» два раза. Выньте его так, чтобы у вас остались {-3, -1, 6, 3}.
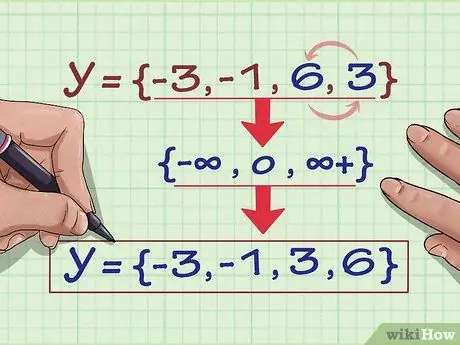
Шаг 4. Запишите диапазон отношения в порядке возрастания
Теперь измените порядок чисел в наборе так, чтобы вы двигались от наименьшего к наибольшему, и у вас есть свой диапазон. Диапазон отношения {(2, -3), (4, 6), (3, -1), (6, 6), (2, 3)} равен {-3, -1, 3, 6}. Все готово.

Шаг 5. Убедитесь, что отношение является функцией
Чтобы отношение было функцией, каждый раз, когда вы вводите одно число координаты x, координата y должна быть одинаковой. Например, отношение {(2, 3) (2, 4) (6, 9)} не является функцией, потому что, когда вы вводите 2 как x в первый раз, вы получаете 3, но во второй раз вы поставьте 2, у вас четверка. Чтобы отношение было функцией, если вы вводите один и тот же ввод, вы всегда должны получать один и тот же вывод. Если вы введете -7, вы должны каждый раз получать одну и ту же координату y (какой бы она ни была).
Метод 4 из 4: определение диапазона функции в задаче Word

Шаг 1. Прочтите задачу
Допустим, вы работаете со следующей проблемой: «Бекки продает билеты на школьное шоу талантов по 5 долларов за штуку. Сумма денег, которую она собирает, зависит от того, сколько билетов она продает. Каков диапазон функции?"

Шаг 2. Запишите проблему как функцию
В этом случае M представляет собой сумму денег, которую она собирает, а t представляет собой количество билетов, которые она продает. Однако, поскольку каждый билет будет стоить 5 долларов, вам придется умножить количество проданных билетов на 5, чтобы найти сумму денег. Следовательно, функцию можно записать как M (t) = 5т.
Например, если она продает 2 билета, вам придется умножить 2 на 5, чтобы получить 10 - сумму в долларах, которую она получит

Шаг 3. Определите домен
Чтобы определить диапазон, необходимо сначала найти домен. Домен - это все возможные значения t, которые работают в уравнении. В этом случае Бекки может продать 0 или более билетов - она не может продавать отрицательные билеты. Поскольку мы не знаем количество мест в ее школьной аудитории, мы можем предположить, что она теоретически может продать бесконечное количество билетов. И она может продавать только целые билеты; например, она не может продать половину билета. Следовательно, область определения функции t = любое неотрицательное целое число.

Шаг 4. Определите диапазон
Диапазон - это возможная сумма денег, которую Бекки может заработать на своей продаже. Вы должны работать с доменом, чтобы найти диапазон. Если вы знаете, что домен - это любое неотрицательное целое число и что формула M (t) = 5 т, то вы знаете, что в эту функцию можно вставить любое неотрицательное целое число, чтобы получить результат или диапазон. Например, если она продает 5 билетов, то M (5) = 5 x 5, или 25 долларов. Если она продаст 100, то M (100) = 5 x 100, или 500 долларов. Следовательно, диапазон функции - любое неотрицательное целое число, кратное пяти.
Это означает, что любое неотрицательное целое число, кратное пяти, является возможным выходом для входа функции
Видео - с помощью этой службы некоторая информация может быть передана YouTube
подсказки
- В более сложных случаях может быть проще сначала нарисовать график с использованием домена (если возможно), а затем определить диапазон графически.
- Посмотрите, сможете ли вы найти обратную функцию. Область определения обратной функции функции равна диапазону этой функции.
- Убедитесь, что функция повторяется. Любая функция, повторяющаяся по оси x, будет иметь одинаковый диапазон для всей функции. Например, f (x) = sin (x) имеет диапазон от -1 до 1.
