Помогая вашему ребенку усвоить концепцию сложения, его или ее академическое будущее будет прочно закреплено. В большинстве штатов есть стандарты, которые стремятся к тому, чтобы все первоклассники знали свои факты сложения (и вычитания) сумм до 20. Однако, прежде чем дети смогут овладеть сложением сумм, им необходимо понять природу «сложения». Разнообразные обучающие инструменты помогут вам эффективно работать с ребенком или в классе и сделать обучение более интересным.
Шаги
Метод 1 из 4: использование манипуляторов

Шаг 1. Используйте объекты, чтобы продемонстрировать, как работает сложение
Дети хорошо реагируют на визуальные инструменты, которые помогают им понять концепции сложения. Можно использовать любой простой в обращении предмет, от бусинок или блоков до Cheerios. Начните с небольшого количества элементов и используйте различные тактики, чтобы продемонстрировать числовые отношения:
- Дайте ребенку две небольшие группы предметов - скажем, группу из двух блоков и группу из трех блоков. Попросите ребенка подсчитать количество блоков в каждой группе.
- Попросите ребенка объединить эти две группы предметов и подсчитать общее количество блоков. Объясните, что он или она «сложили» эти группы вместе.
- Предоставьте определенное количество предметов - например, шесть Cheerios - и спросите вашего ребенка, сколькими способами он или она может объединить группы Cheerios, чтобы получилось шесть. Например, она может создать одну группу из пяти Cheerios и одну группу из одного человека.
- Продемонстрируйте, как можно «добавить» к группе объектов путем наложения их друг на друга. Например, начните со стопки из трех пенни и добавьте еще два в стопку. Попросите ребенка подсчитать, сколько пенни сейчас в стопке.

Шаг 2. Группируйте детей и используйте их тела как человеческие «манипуляторы»
«В классной комнате воспользуйтесь необходимостью ваших юных учеников регулярно передвигаться, используя их как человеческие манипуляторы. Используйте тактику, аналогичную той, которую вы использовали бы с объектами, чтобы группировать и объединять учеников, чтобы они считали себя в различных конфигурациях. (Сгруппировать студентов не рекомендуется!)

Шаг 3. Подумайте о том, чтобы дети сами создавали свои манипуляторы
Используйте пластилин для создания манипулятивных предметов или объедините дополнительный урок с уроком искусства использования ножниц, чтобы создать коллекцию бумажных фигур.

Шаг 4. Используйте игровые элементы по-новому для создания дополнительных игр
Игральные кости легко поддаются начальным играм с добавлением. Попросите учащихся бросить два кубика и попрактиковаться в сложении полученных чисел. Вы также можете использовать игральные карты или домино.
При работе с группами учащихся с разными способностями вы можете адаптировать эту игру, чтобы усложнить задачу тем, кто быстро учится. Попросите их сложить результаты трех или более игральных костей или игральных карт
Шаг 5. Считайте монетами
Используйте деньги, чтобы попрактиковаться в сложении единиц, пятерок, десятков и даже с интервалом по 25. Эта тактика учит денежным навыкам в дополнение к сложению и имеет дополнительное преимущество в демонстрации практических преимуществ обучения сложению.
Метод 2 из 4: знакомство с математическим языком и "фактическими семьями"
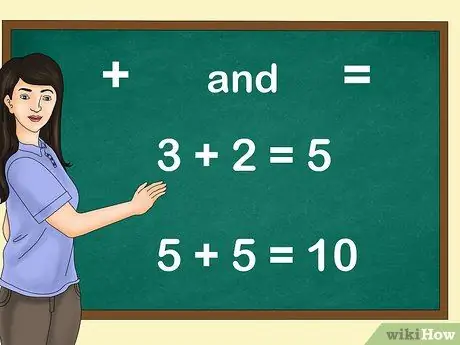
Шаг 1. Ознакомьте детей с дополнительными символами
Объясните им значение символов «+» и «=». Затем помогите им научиться писать простые «числовые предложения» - например, «3 + 2 = 5».
Начните с предложений с горизонтальными цифрами. Маленькие дети уже учатся тому, что они должны писать слова и предложения «поперек» бумаги. Подобная практика с числовыми предложениями будет менее запутанной. Когда дети усвоят эту концепцию, вы можете ввести концепцию вертикальных сумм
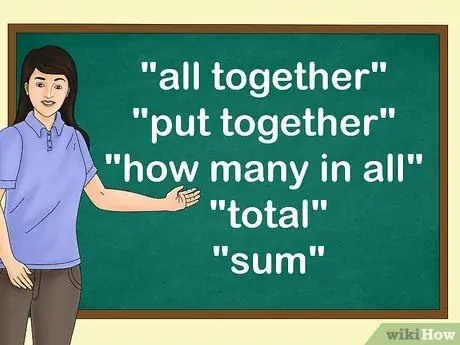
Шаг 2. Научите детей словам, которые означают «сложение»
«Введите такие термины, как« все вместе »,« вместе »,« сколько всего »,« всего »и« сумма », которые обычно указывают на то, что ребенку нужно будет сложить два или более чисел.
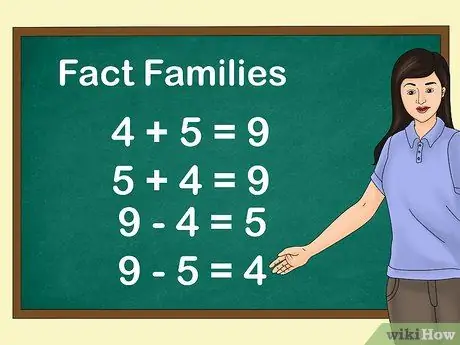
Шаг 3. Используйте «семьи фактов», чтобы помочь детям понять числовые отношения
Семейства фактов показывают, как соотносятся друг с другом различные числа в задаче сложения. Семейства фактов часто включают в себя как сложение, так и вычитание, чтобы помочь учащимся понять обратную связь между этими двумя навыками. Например, целые числа 4, 5 и 9 являются «семейством фактов», потому что 4 + 5 = 9; 5 + 4 = 9; 9 - 4 = 5; и 9-5 = 4.
Подумайте об использовании картонных упаковок из-под молока, чтобы проиллюстрировать «семейные факты». Накройте картонные коробки бумагой или протрите поверхность, если вы хотите повторно использовать картонные коробки. Попросите учащихся перечислить целые числа группы фактов наверху коробки - например, 4, 5 и 9. Затем попросите их написать по одному факту из «группы фактов» этих чисел на каждой из четырех сторон коробки
Метод 3 из 4: запоминание основных фактов

Шаг 1. Научите детей «пропускать счет»
Обучение счету от двоек, пятерок и десятков до 100 улучшит понимание вашим ребенком числовых соотношений и начнет давать простые ориентиры.

Шаг 2. Поощряйте детей запоминать «двойники»
«Двойники» - это математические факты, такие как «3 + 3 = 6» или «8 + 8 = 16.» Опять же, эти факты служат легкими ориентирами, когда учащиеся учатся складывать. Ребенок, который инстинктивно знает, что «8 + 8 = 16, например, легче вычислить сумму «8 + 9», просто прибавив единицу к общей сумме.

Шаг 3. Используйте флеш-карточки, чтобы стимулировать запоминание
Попробуйте сгруппировать карточки по семействам фактов, чтобы подчеркнуть взаимосвязь между этими числами. Студенты должны понимать, как числа взаимодействуют друг с другом, а запоминание основных математических фактов наизусть обеспечит дополнительную основу для перехода к более сложной арифметике.
Метод 4 из 4: использование проблем со словами

Шаг 1. Попрактикуйтесь в различных типах задач-рассказов
В то время как некоторые учащиеся могут находить сюжетные задачи более сложными, другие будут преуспевать, когда они лучше поймут реальные последствия дополнительного обучения. Помогите ребенку распознать три разные ситуации, требующие дополнения:
- Задачи «Результат неизвестен» - например, если у Мередит две машины, а в день своего рождения она получает еще три, сколько машин у нее сейчас всего?
- Задачи «Изменить неизвестное» - например, если у Мередит две машины, и после открытия всех подарков на день рождения у нее теперь пять машин, сколько машин она получила на свой день рождения?
- Проблемы с «неизвестным запуском» - например, если Мередит получает три машины на свой день рождения, а теперь у нее пять, сколько машин у нее было в начале?

Шаг 2. Научите детей распознавать проблемы «соединить», «частично-частично-целое» и «сравнить»
Ситуации реального мира будут иметь разные параметры. Понимание того, как это работает, поможет вашему ребенку разработать инструменты для решения дополнительных задач.
- «Объединенные» задачи предполагают рост количества. Например, если Элизабет испечет три торта, а Сара - еще шесть, сколько всего тортов получится? В задачах «Соединение» учащихся также могут попросить решить для неизвестных изменений или начальных цифр - например, если Элизабет испечет три торта, а Элизабет и Сара - девять тортов, сколько тортов испекла Сара?
- Задачи «часть-часть-целое» включают добавление двух статических фигур. Например, если в классе 12 девочек и 10 мальчиков, сколько всего учеников в классе?
- «Проблемы сравнения» связаны с неизвестным в сравниваемом наборе значений. Например, если у Джеффа семь файлов cookie, а у него на три cookie больше, чем у Лауры, сколько файлов cookie у Лауры?

Шаг 3. Используйте книги, изучающие концепции сложения
Детям, ориентированным на чтение и письмо, особенно полезны книги, включающие дополнительные темы. Выполните поиск в Интернете по запросу «учебное дополнение с помощью книг», чтобы получить доступ к спискам полезных томов, составленным преподавателями.
