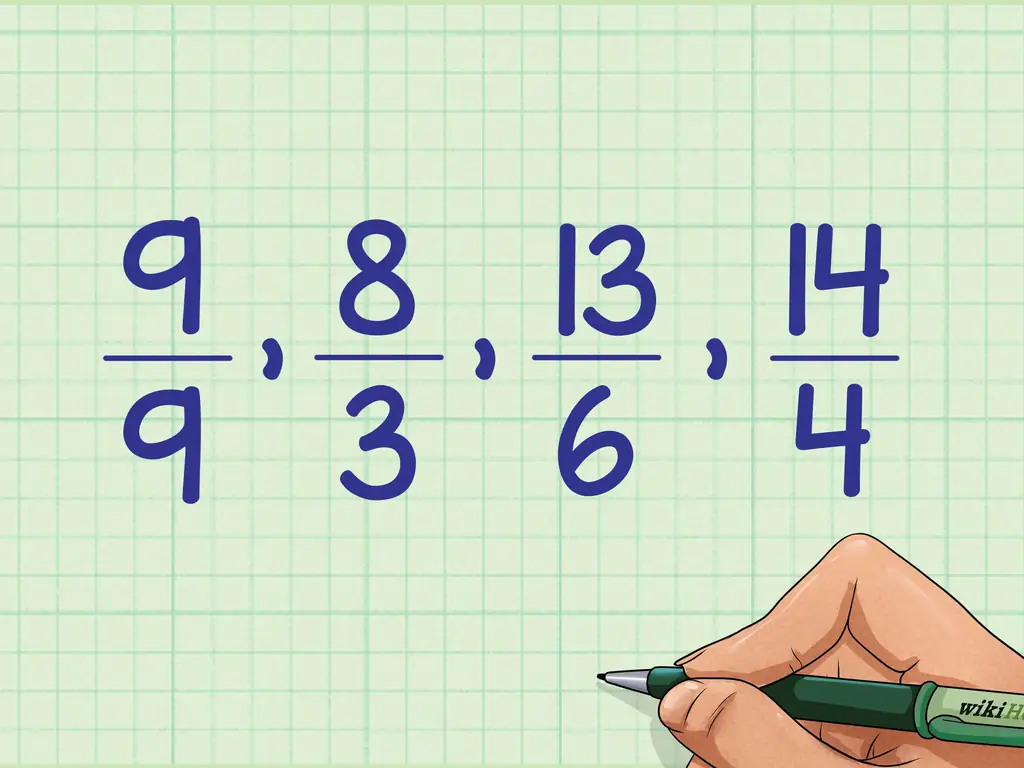В то время как целые числа, такие как 1, 3 и 8, легко упорядочить по размеру, дроби бывает сложно измерить с первого взгляда. Если каждое меньшее число или знаменатель одинаковы, вы можете упорядочить их как целые числа, например 1/5, 3/5 и 8/5. В противном случае вы можете изменить свой список дробей, чтобы использовать тот же знаменатель, не меняя размер какой-либо дроби. Это становится проще с практикой, и вы также можете изучить пару «трюков», сравнивая всего две дроби или когда вы сортируете «неправильные» дроби с тяжелым верхним числом, такие как 7/3.
Шаги
Метод 1 из 3: заказ любого количества дробей

Шаг 1. Найдите общий знаменатель для всех дробей
Используйте один из этих методов, чтобы найти знаменатель или меньшее число дроби, которое вы можете использовать, чтобы переписать каждую дробь в списке, чтобы вы могли легко их сравнить. Это называется общим знаменателем или наименьшим общим знаменателем, если он является наименьшим из возможных:
-
Умножьте все знаменатели вместе. Например, если вы сравниваете 2/3, 5/6 и 1/3, умножьте два разных знаменателя: 3 x 6 =
Шаг 18.. Это простой метод, но он часто дает гораздо большее количество, чем другие методы, с которыми может быть сложно работать.
-
Или перечислите кратные каждого знаменателя в отдельном столбце, пока не заметите число, которое отображается в каждом столбце. Используйте этот номер. Например, сравнивая 2/3, 5/6 и 1/3, перечислите несколько кратных 3: 3, 6, 9, 12, 15, 18. Затем перечислите кратные 6: 6, 12, 18. Поскольку
Шаг 18. отображается в обоих списках, используйте этот номер. (Вы также можете использовать 12, но в приведенных ниже примерах предполагается, что вы используете 18.)

Шаг 2. Преобразуйте каждую дробь так, чтобы она использовала общий знаменатель
Помните, что если вы умножите верхнюю и нижнюю части дроби на одинаковую величину, дробь останется того же размера. Используйте эту технику для каждой дроби, одну за другой, чтобы каждая дробь использовала общий знаменатель в качестве нижнего числа. Попробуйте это для 2/3, 5/6 и 1/3, используя общий знаменатель 18:
- 18 ÷ 3 = 6, поэтому 2/3 = (2x6) / (3x6) = 12/18
- 18 ÷ 6 = 3, поэтому 5/6 = (5x3) / (6x3) = 15/18
- 18 ÷ 3 = 6, поэтому 1/3 = (1x6) / (3x6) = 6/18
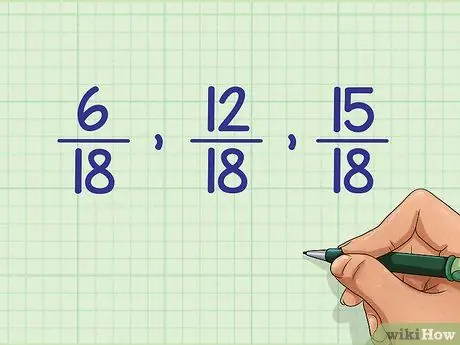
Шаг 3. Используйте верхнее число, чтобы упорядочить дроби
Теперь, когда у всех одинаковый знаменатель, дроби легко сравнивать. Используйте их верхнее число или числитель, чтобы расположить их от наименьшего к наибольшему. Ранжируя найденные выше дроби, получаем: 6/18, 12/18, 15/18.

Шаг 4. Верните каждую дробь в ее первоначальный вид
Сохраните дроби в том же порядке, но верните каждой из них исходную форму. Вы можете сделать это, вспомнив, как преобразовывалась каждая дробь, или снова разделив верх и низ каждой дроби:
- 6/18 = (6 ÷ 6)/(18 ÷ 6) = 1/3
- 12/18 = (12 ÷ 6)/(18 ÷ 6) = 2/3
- 15/18 = (15 ÷ 3)/(18 ÷ 3) = 5/6
- Ответ: «1/3, 2/3, 5/6».
Метод 2 из 3: упорядочивание двух дробей с помощью перекрестного умножения
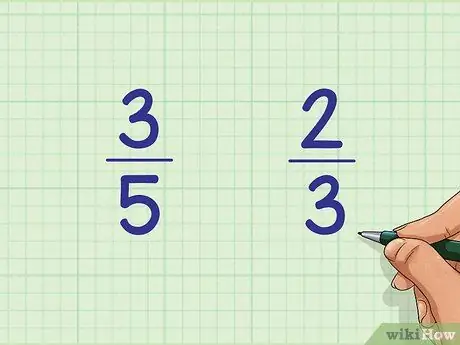
Шаг 1. Напишите две дроби рядом друг с другом
Например, сравните дробь 3/5 и дробь 2/3. Напишите эти строки рядом друг с другом на странице: 3/5 слева и 2/3 справа.
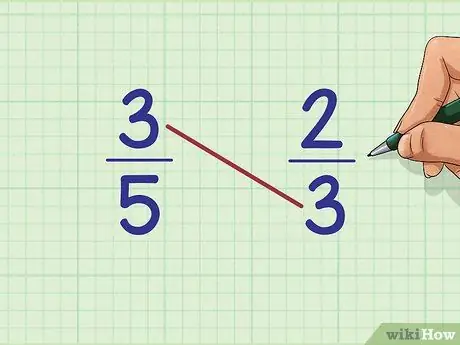
Шаг 2. Умножьте верхнюю часть первой дроби на нижнюю часть второй дроби
В нашем примере верхнее число или числитель первой дроби (3/5) равно
Шаг 3.. Нижнее число или знаменатель второй дроби (2/3) - это als
Шаг 3.. Умножьте их вместе: 3 x 3 =?
Этот метод называется перекрестным умножением, потому что вы умножаете числа, расположенные по диагонали друг напротив друга
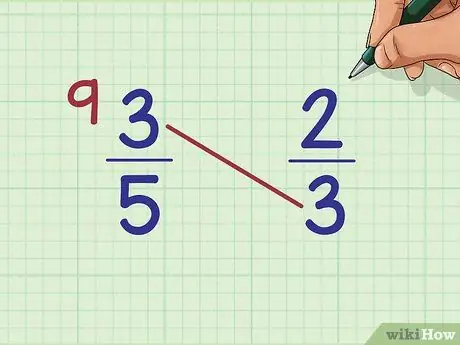
Шаг 3. Напишите свой ответ рядом с первой дробью
Напишите произведение или ответ на задачу умножения рядом с первой дробью на странице. В нашем примере 3 x 3 = 9, поэтому вы должны написать
Шаг 9. рядом с первой дробью в левой части страницы.
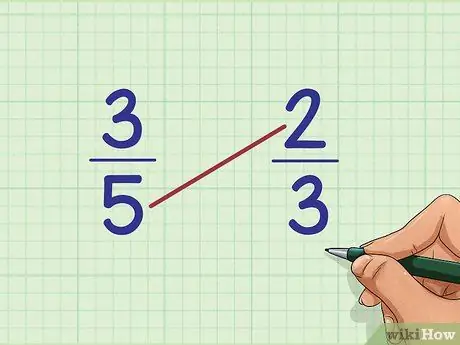
Шаг 4. Умножьте верхнюю часть второй дроби на нижнюю часть первой
Чтобы узнать, какая дробь больше, нам нужно сравнить наш ответ выше с ответом на другую задачу умножения. Умножьте эти два числа вместе. В нашем примере (сравнивая 3/5 и 2/3) умножьте 2 x 5 вместе.

Шаг 5. Напишите этот ответ рядом со второй дробью
Напишите ответ на эту вторую задачу умножения рядом со второй дробью. В этом примере ответ - 10.
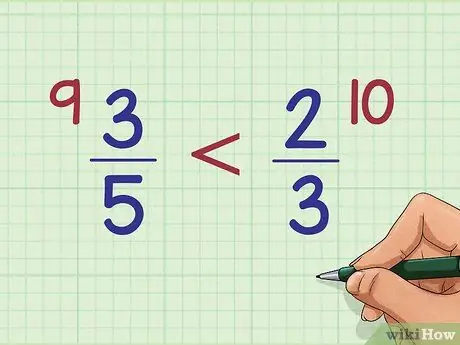
Шаг 6. Сравните значения двух перекрестных произведений
Ответы на проблемы умножения в этом методе называются перекрестными произведениями. Если одно перекрестное произведение больше другого, то дробь, следующая за этим перекрестным произведением, также больше, чем другая дробь. В нашем примере, поскольку 9 меньше 10, это означает, что 3/5 должно быть меньше 2/3.
Помните, всегда указывайте перекрестное произведение рядом с дробью, верхнее число которой вы использовали
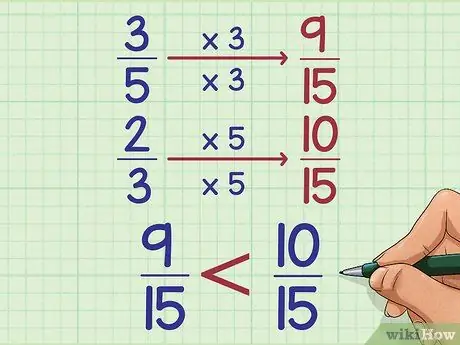
Шаг 7. Понять, почему это работает
Чтобы сравнить две дроби, обычно вы преобразуете их, чтобы получить одинаковый знаменатель или меньшую часть дроби. Втайне это то, что делает кросс-умножение! Он просто пропускает фактическую запись знаменателей, поскольку, как только две дроби имеют одинаковое значение, вам нужно сравнить только два верхних числа. Вот наш тот же пример (3/5 против 2/3), написанный без "ярлыка" перекрестного умножения:
- 3/5 = (3x3) / (5x3) = 9/15
- 2/3 = (2x5) / (3x5) = 10/15
- 9/15 меньше, чем 10/15
- Следовательно, 3/5 меньше 2/3
Метод 3 из 3: упорядочивание дробей больше единицы
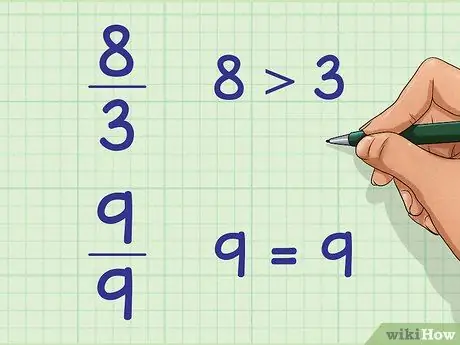
Шаг 1. Используйте это для дробей, верхнее число которых равно или больше нижнего числа
Если у дроби верхнее число или числитель больше нижнего числа или знаменателя, оно больше единицы. 8/3 - один из примеров этого типа дроби. Вы также можете использовать это для дробей с равным числителем и знаменателем, например 9/9. Обе эти дроби являются примерами неправильных дробей.
Вы все еще можете использовать другие методы для этих дробей. Однако этот метод помогает понять эти дроби и может быть быстрее
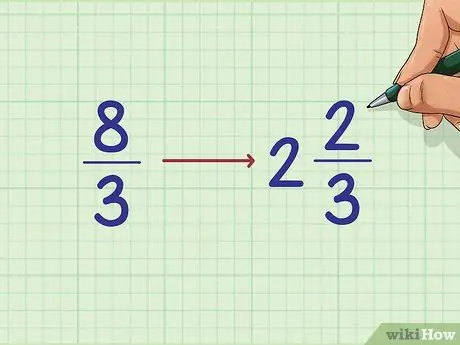
Шаг 2. Преобразуйте каждую неправильную дробь в смешанное число
Превратите их в смесь целых чисел и дробей. Иногда у вас может получиться сделать это в уме. Например, 9/9 = 1. В других случаях используйте длинное деление, чтобы узнать, сколько раз числитель попадает в знаменатель без остатка. Остаток в этой задаче деления в столбик, если таковой имеется, «остается» в виде дроби. Например:
- 8/3 = 2 + 2/3
- 9/9 = 1
- 19/4 = 4 + 3/4
- 13/6 = 2 + 1/6
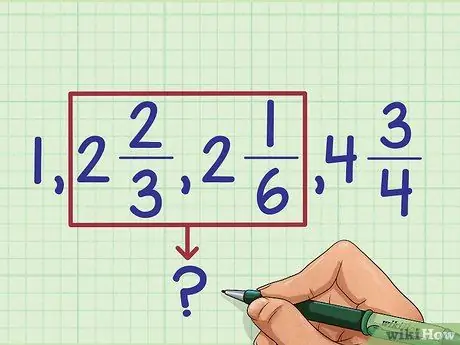
Шаг 3. Отсортируйте смешанные числа по целому числу
Теперь, когда нет неправильных дробей, вы лучше понимаете, насколько велико каждое число. Пока не обращайте внимания на дроби и отсортируйте дроби по группам по целому числу:
- 1 самый маленький
- 2 + 2/3 и 2 + 1/6 (мы еще не знаем, что больше другого)
- 4 + 3/4 - самый большой

Шаг 4. При необходимости сравните фракции в каждой группе
Если у вас есть несколько смешанных чисел с одним и тем же целым числом, например 2 + 2/3 и 2 + 1/6, сравните дробную часть числа, чтобы увидеть, какое из них больше. Для этого вы можете использовать любой из методов, описанных в других разделах. Вот пример сравнения 2 + 2/3 и 2 + 1/6 с преобразованием дробей к одному знаменателю:
- 2/3 = (2x2) / (3x2) = 4/6
- 1/6 = 1/6
- 4/6 больше 1/6
- 2 + 4/6 больше 2 + 1/6
- 2 + 2/3 больше 2 + 1/6
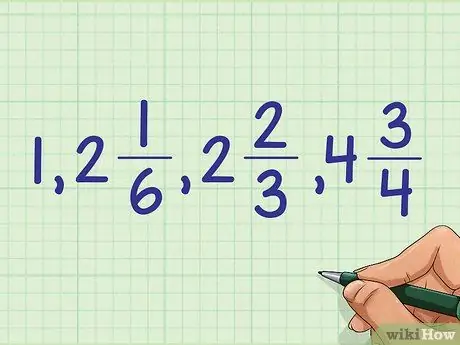
Шаг 5. Используйте свои результаты, чтобы отсортировать весь список смешанных чисел
После того, как вы отсортировали дроби в каждой группе смешанных чисел, вы можете отсортировать весь список: 1, 2 + 1/6, 2 + 2/3, 4 + 3/4.
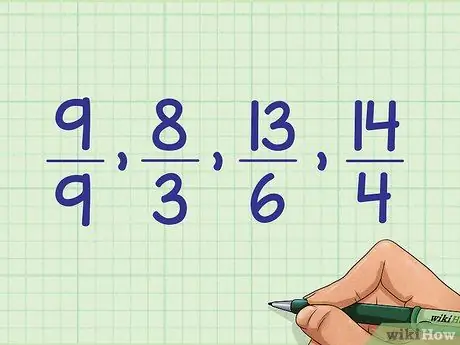
Шаг 6. Преобразуйте смешанные числа обратно в их исходные дроби
Сохраните порядок в том же порядке, но отмените внесенные вами изменения и запишите числа как исходные неправильные дроби: 9/9, 8/3, 13/6, 19/4.
Видео - с помощью этой службы некоторая информация может быть передана YouTube
подсказки
- Если числители совпадают, вы можете выполнить сортировку в обратном порядке знаменателя. Например, 1/8 <1/7 <1/6 <1/5. Думайте об этом как о пицце: если вы перейдете от 1/2 к 1/8, вы разрежете пиццу на 8 ломтиков вместо 2, и 1 ломтик, который вы получите, теперь намного меньше.
- При заказе большого количества фракций может быть полезно сравнивать и заказывать меньшие группы из 2, 3 или 4 фракций за раз.
- Хотя поиск наименьшего общего знаменателя полезен, так как вы можете работать с меньшими числами, любой общий знаменатель будет работать. Попробуйте отсортировать 2/3, 5/6 и 1/3, используя общий знаменатель 36, и посмотрите, получите ли вы тот же результат.