В математике факторинг это процесс поиска чисел или выражений, которые умножаются вместе, чтобы получить данное число или уравнение. Факторинг - полезный навык для решения основных задач алгебры; способность грамотно разложить множители становится почти необходимой при работе с квадратными уравнениями и другими формами многочленов. Факторинг может использоваться для упрощения алгебраических выражений и упрощения решения. Факторинг может даже дать вам возможность исключать некоторые возможные ответы намного быстрее, чем вы могли бы решить вручную.
Шаги
Метод 1 из 3: разложение чисел на множители и основные алгебраические выражения

Шаг 1. Понять определение факторинга применительно к отдельным числам
Факторинг концептуально прост, но на практике может оказаться сложной задачей при применении к сложным уравнениям. Из-за этого проще всего подойти к концепции факторинга, начав с простых чисел, затем перейти к простым уравнениям, прежде чем, наконец, перейти к более сложным приложениям. Факторы данного числа - это числа, которые умножаются, чтобы получить это число. Например, множители 12 равны 1, 12, 2, 6, 3 и 4, потому что 1 × 12, 2 × 6 и 3 × 4 равны 12.
- Другой способ думать об этом состоит в том, что множители данного числа - это числа, на которые оно делится без остатка.
-
Сможете ли вы найти все множители числа 60? Мы используем число 60 для самых разных целей (минуты в часе, секунды в минуте и т. Д.), Потому что оно делится без остатка на довольно широкий диапазон чисел.
Множители 60: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 и 60

Шаг 2. Поймите, что выражения переменных также могут быть факторизованы
Факторизация может осуществляться как одиночные числа, так и переменные с числовыми коэффициентами. Для этого просто найдите множители коэффициента переменной. Знание того, как факторизовать переменные, полезно для упрощения алгебраических уравнений, частью которых являются переменные.
-
Например, переменная 12x может быть записана как произведение множителей 12 и x. Мы можем записать 12x как 3 (4x), 2 (6x) и т. Д., Используя любой множитель 12, который лучше всего подходит для наших целей.
Мы можем даже многократно множить множитель в 12 раз. Другими словами, нам не нужно останавливаться на 3 (4x) или 2 (6x) - мы можем множить 4x и 6x, чтобы получить 3 (2 (2x) и 2 (3 (2x) соответственно. Очевидно, что эти два выражения равны

Шаг 3. Примените дистрибутивное свойство умножения к фактор-алгебраическим уравнениям
Используя свои знания о том, как разложить на множители как одиночные числа, так и переменные с коэффициентами, вы можете упростить простые алгебраические уравнения, найдя факторы, которые являются общими для чисел и переменных в алгебраическом уравнении. Обычно, чтобы сделать уравнение как можно более простым, мы пытаемся найти наибольший общий фактор. Этот процесс упрощения возможен благодаря распределительному свойству умножения, которое гласит, что для любых чисел a, b и c, а (Ь + с) = ab + ac.
- Попробуем на примере задачи. Чтобы разложить на множители алгебраическое уравнение 12 x + 6, сначала давайте попробуем найти наибольший общий делитель 12x и 6. 6 - это наибольшее число, которое делится на 12x и 6, поэтому мы можем упростить уравнение до 6 (2x + 1).
- Этот процесс также применяется к уравнениям с отрицательными числами и дробями. Например, x / 2 + 4 можно упростить до 1/2 (x + 8), а -7x + -21 можно разложить на множители до -7 (x + 3).
Метод 2 из 3: разложение квадратных уравнений на множители

Шаг 1. Убедитесь, что уравнение имеет квадратичную форму (ax2 + bx + c = 0).
Квадратные уравнения имеют вид ax2 + bx + c = 0, где a, b и c - числовые константы, а a не равно 0 (обратите внимание, что a может быть равно 1 или -1). Если у вас есть уравнение, содержащее одну переменную (x), которая имеет один или несколько членов x во второй степени, вы обычно можете переместить члены в уравнении, используя базовые алгебраические операции, чтобы получить 0 с одной стороны от знака равенства и топора2и т. д. с другой стороны.
- Например, рассмотрим алгебраическое уравнение. 5x2 + 7x - 9 = 4x2 + x - 18 можно упростить до x2 + 6x + 9 = 0, который находится в квадратичной форме.
- Уравнения с большими степенями x, например x3, Икс4и т. д. не могут быть квадратными уравнениями. Это кубические уравнения, уравнения четвертой степени и т. Д., Если уравнение не может быть упрощено, чтобы исключить эти члены x, превышающие степень двойки.

Шаг 2. В квадратных уравнениях, где a = 1, множитель на (x + d) (x + e), где d × e = c и d + e = b
Если ваше квадратное уравнение имеет вид x2 + bx + c = 0 (другими словами, если коэффициент при x2 term = 1), возможно (но не гарантируется), что можно будет использовать относительно простой ярлык для разложения уравнения на множители. Найдите два числа, которые умножаются, чтобы получить c а также добавить, чтобы получить b. Найдя эти два числа d и e, поместите их в следующее выражение: (х + г) (х + е). Эти два члена, умноженные вместе, образуют ваше квадратное уравнение - другими словами, они являются множителями вашего квадратного уравнения.
- Например, рассмотрим квадратное уравнение x2 + 5x + 6 = 0. 3 и 2 умножаются вместе, чтобы получить 6, а также складывать, чтобы получить 5, поэтому мы можем упростить это уравнение до (x + 3) (x + 2).
-
Существуют небольшие вариации этого базового ярлыка для небольших вариаций самого уравнения:
- Если квадратное уравнение имеет вид x2-bx + c, ваш ответ будет в такой форме: (x - _) (x - _).
- Если он имеет вид x2+ bx + c, ваш ответ выглядит так: (x + _) (x + _).
- Если он имеет вид x2-bx-c, вы ответите в форме (x + _) (x - _).
- Примечание: числа в пробелах могут быть дробными или десятичными. Например, уравнение x2 + (21/2) x + 5 = 0 множителей на (x + 10) (x + 1/2).

Шаг 3. Если возможно, проанализируйте осмотром
Вы не поверите, но для простых квадратных уравнений одним из общепринятых способов разложения на множители является простое изучение проблемы, а затем рассмотрение возможных ответов до тех пор, пока вы не найдете правильный. Это также известно как факторинг путем проверки. Если уравнение имеет вид ax2+ bx + c и a> 1, ваш факторизованный ответ будет в форме (dx +/- _) (ex +/- _), где d и e - ненулевые числовые константы, которые умножаются, чтобы получить a. Либо d, либо e (или оба) могут быть числом 1, хотя это не обязательно так. Если оба равны 1, вы, по сути, использовали ярлык, описанный выше.
Рассмотрим пример задачи. 3x2 - 8x + 4 сначала кажется устрашающим. Однако, когда мы понимаем, что 3 имеет только два фактора (3 и 1), это становится проще, потому что мы знаем, что наш ответ должен быть в форме (3x +/- _) (x +/- _). В этом случае добавление -2 к обоим пробелам дает правильный ответ. -2 × 3x = -6x и -2 × x = -2x. -6x и -2x прибавить к -8x. -2 × -2 = 4, поэтому мы можем видеть, что разложенные на множители члены в скобках умножаются, чтобы стать исходным уравнением.

Шаг 4. Решите, заполнив квадрат
В некоторых случаях квадратные уравнения можно быстро и легко разложить на множители с помощью специального алгебраического тождества. Любое квадратное уравнение вида x2 + 2xh + h2 = (х + ч)2. Итак, если в вашем уравнении ваше значение b в два раза больше квадратного корня из вашего значения c, ваше уравнение может быть разложено на (x + (sqrt (c)))2.
Например, уравнение x2 + 6x + 9 соответствует этой форме. 32 равно 9, а 3 × 2 равно 6. Итак, мы знаем, что факторизованная форма этого уравнения равна (x + 3) (x + 3) или (x + 3)2.
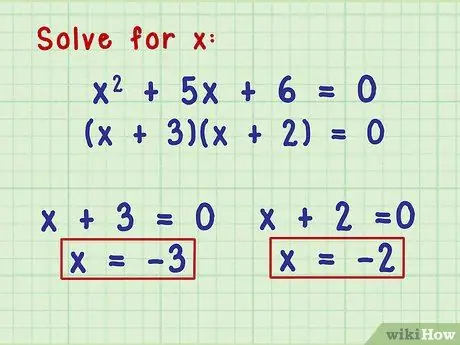
Шаг 5. Используйте множители для решения квадратных уравнений
Независимо от того, как вы факторизуете свое квадратичное выражение, после его факторизации вы можете найти возможные ответы для значения x, установив каждый коэффициент равным нулю и решив. Поскольку вы ищете значения x, которые приводят к тому, что ваше уравнение равно нулю, значение x, при котором любой из ваших факторов равен нулю, является возможным ответом для вашего квадратного уравнения.
Вернемся к уравнению x2 + 5x + 6 = 0. Это уравнение разложено на (x + 3) (x + 2) = 0. Если один из множителей равен 0, все уравнение равно 0, поэтому наши возможные ответы для x - это числа, которые делают (x + 3) и (x + 2) равны 0. Эти числа равны -3 и -2 соответственно.

Шаг 6. Проверьте свои ответы - некоторые из них могут быть посторонними
Когда вы найдете возможные ответы для x, снова подключите их к исходному уравнению, чтобы проверить, верны ли они. Иногда ответы, которые вы найдете, не приводят к тому, что исходное уравнение при повторном подключении не становится равным нулю. Мы называем эти ответы посторонними и игнорируем их.
-
Подключим -2 и -3 к x2 + 5x + 6 = 0. Во-первых, -2:
- (-2)2 + 5(-2) + 6 = 0
- 4 + -10 + 6 = 0
- 0 = 0. Это правильно, поэтому -2 - правильный ответ.
-
Теперь попробуем -3:
- (-3)2 + 5(-3) + 6 = 0
- 9 + -15 + 6 = 0
- 0 = 0. Это тоже правильно, поэтому -3 тоже правильный ответ.
Метод 3 из 3: Факторинг других форм уравнений

Шаг 1. Если уравнение имеет вид a2-b2, разложим его на (a + b) (a-b).
Уравнения с двумя переменными имеют разные факторы, чем базовые квадраты. Для любого уравнения a2-b2 где a и b не равны 0, уравнение множится в (a + b) (a-b).
Например, уравнение 9x2 - 4 года2 = (3x + 2y) (3x - 2y).

Шаг 2. Если уравнение имеет вид a2+ 2ab + b2, множим его на (a + b)2.
Обратите внимание: если трехчлен имеет форму2-2ab + b2, факторизованная форма немного отличается: (a-b)2.
Уравнение 4x2 + 8xy + 4y2 можно переписать как 4x2 + (2 × 2 × 2) ху + 4у2. Теперь мы можем видеть, что это в правильной форме, поэтому мы можем с уверенностью сказать, что наше уравнение множителей на (2x + 2y)2

Шаг 3. Если уравнение имеет вид a3-b3, разложим его на (a-b) (a2+ ab + b2).
Наконец, стоит упомянуть, что кубики и даже уравнения более высокого порядка могут быть разложены на множители, хотя процесс факторизации быстро становится чрезмерно сложным.
Например, 8x3 - 27 лет3 множители к (2x - 3y) (4x2 + ((2x) (3y)) + 9y2)
Видео - с помощью этой службы некоторая информация может быть передана YouTube
подсказки
- а2-b2 факторизован, а2+ b2 не подлежит фактурированию.
- Помните, как разложить константы на множители - это может помочь.
- Остерегайтесь дробей в процессе факторинга и работайте с ними правильно и аккуратно.
- Если у вас есть трехчлен в виде x2+ bx + (b / 2)2, факторизованная форма (x + (b / 2))2. (У вас может возникнуть такая ситуация при завершении квадрата.)
- Помните, что a0 = 0 (свойство нулевого продукта).
