В конце концов, вы окажетесь в ситуации, когда вам придется решать математическую задачу без калькулятора. Попытка представить себе ручку и бумагу в своей голове часто мало помогает. К счастью, есть более быстрые и простые способы делать расчеты в уме, и они часто решают проблему более осмысленно, чем то, чему вы научились в школе. Независимо от того, являетесь ли вы учеником, находящимся в состоянии стресса, или мастером математики, ищущим еще более быстрые трюки, каждый найдет что-то, чему можно научиться.
Шаги
Метод 1 из 12. Разбейте задачи на сложение и вычитание на части

4 1 Скоро в продаже
Шаг 1. Сложите по отдельности разряды сотен, десятков и единиц
Относитесь к каждой группе как к отдельной проблеме:
- 712 + 281 → «700 + 200», «10 + 80» и «2 + 1»
-
700 + 200 =
Шаг 9.00, затем 10 + 80
Шаг 9.0, затем 2 + 1
Шаг 3.
- 900 + 90 + 3 = 993.
- Если вместо однозначных цифр использовать «сотни» или «десятки», будет легче отслеживать, когда сумма цифр превышает десять. Например, для 37 + 45 подумайте «30 + 40 = 70» и «7 + 5 = 12». Затем прибавьте 70 + 12, чтобы получить 82.
Метод 2 из 12: Измените задачу на округление чисел

1 9 Скоро в продаже
Шаг 1. Отрегулируйте, чтобы получить круглые числа, а затем исправьте после того, как проблема будет решена
Большинство из нас работает с круглыми числами намного быстрее. Запомните внесенные вами изменения, чтобы вы могли откорректироваться и получить точный ответ в конце. Например:
- Дополнение: Для 596 + 380 пойми, что ты можешь добавить 4 до 596, чтобы округлить до 600, затем прибавить 600 + 380, чтобы получить 980. Отмените округление на вычитая 4 от 980 получить 976.
- Вычитание: для 815 - 521, разбейте его на 800-500, 10-20 и 5-1. Чтобы превратить неудобное «10-20» в «20-20», прибавь 10 к 815 чтобы получить 825. Теперь решите, чтобы получить 304, затем отмените округление на вычитая 10 получить 294.
- Умножение: для 38 х 3, вы можете прибавь 2 к 38 чтобы получить задачу 40 x 3, что составляет 120. Поскольку добавленные вами 2 были умножены на три, вам нужно отменить округление на вычитая 2 x 3 = 6 в конце получим 120 - 6 = 114.
Метод 3 из 12: научитесь складывать сразу несколько чисел
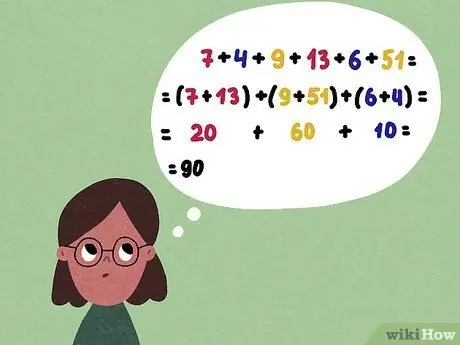
1 7 Скоро в продаже
Шаг 1. Измените порядок чисел, чтобы получить удобные суммы
Проблема сложения одинакова, независимо от того, в каком порядке вы ее решаете. Ищите числа, которые в сумме дают 10 или другие красивые круглые числа:
Например, 7 + 4 + 9 + 13 + 6 + 51 можно преобразовать в (7 + 13) + (9 + 51) + (6 + 4) = 20 + 60 + 10 = 90
Метод 4 из 12: умножьте слева направо

0 4 Скоро в продаже
Шаг 1. Следите за сотнями, десятками и единицами мест
На бумаге большинство людей умножают единицы, занимающие первое место, справа налево. Но в голове проще пойти другим путем:
- Для 453 х 4, начните с 400 x 4 = 1600, затем 50 x 4 = 200, затем 3 x 4 = 12. Сложите их все вместе, чтобы получить 1812.
- Если в обоих числах больше одной цифры, вы можете разбить их на части. Каждая цифра должна умножаться друг на друга, поэтому уследить за всем может быть сложно. 34 х 12 = (34 x 10) + (34 x 2), которое можно разбить на (30 x 10) + (4 x 10) + (30 x 2) + (4 x 2) = 300 + 40 + 60 + 8 = 408.
Метод 5 из 12: попробуйте быстрое умножение чисел с 11 по 19

0 2 Скоро в продаже
Шаг 1. Попробуйте этот метод превратить одну сложную задачу в две более простые
Это еще один способ разбить проблему на части. Сначала это может быть немного сложно запомнить, но как только вы это усвоите, умножение станет намного быстрее. Это проще всего при умножении двух чисел, которые находятся в диапазоне от 11 до 19, но вы можете научиться использовать его для других задач:
- Давайте посмотрим на числа, близкие к 10, например 13 х 15. Вычтите 10 из второго числа, затем прибавьте свой ответ к первому: 15-10 = 5 и 13 + 5 = 18.
- Умножьте свой ответ на десять: 18 x 10 = 180.
- Затем вычтите десять с обеих сторон и умножьте результат: 3 x 5 = 15.
- Сложите два ответа, чтобы получить окончательный ответ: 180 + 15 = 195.
- Осторожно с меньшими числами! Для 13 x 8 вы начинаете с «8-10 = -2», затем «13 + -2 = 11». Если сложно работать с отрицательными числами в голове, попробуйте другой метод решения подобных задач.
- Для больших чисел будет проще использовать «базовое число», например 20 или 30, вместо 10. Если вы попробуете это сделать, убедитесь, что вы используете это число везде, где 10 используется выше. Например, для 21 x 24 вы начинаете с добавления 21 + 4, чтобы получить 25. Теперь умножьте 25 на 20 (вместо десяти), чтобы получить 500, и добавьте 1 x 4 = 4, чтобы получить 504.
Метод 6 из 12. Упростите задачи, используя числа, оканчивающиеся на ноль
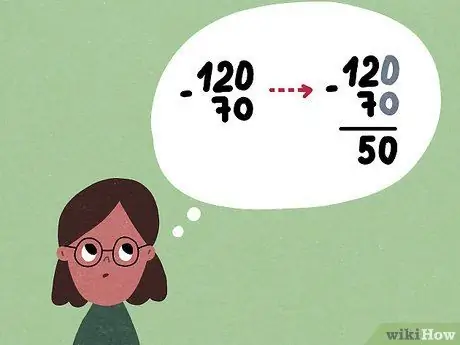
0 3 Скоро в продаже
Шаг 1. Если числа заканчиваются нулями, их можно игнорировать до конца:
- Дополнение: Если все числа имеют нули в конце, вы можете игнорировать общие нули, которые у них есть, и восстанавливать их в конце. 850 + 120 → 85 + 12 = 97, затем восстанавливаем общий ноль: 970.
- Вычитание работает так же: 1000 - 700 → 10-7 = 3, затем восстановите два общих нуля, чтобы получить 300. Обратите внимание, что вы можете удалить только два нуля, которые являются общими для чисел, и должны оставить третий ноль из 1000.
- Умножение: игнорируйте все нули, затем восстанавливайте каждый по отдельности. 3000 х 50 → 3 x 5 = 15, затем восстановите все четыре нуля, чтобы получить 150, 000.
-
Деление: вы можете удалить все общие нули, и ответ будет таким же. 60, 000 ÷ 12, 000 = 60 ÷ 12 =
Шаг 5.. Не добавляйте снова нули.
Метод 7 из 12: легко умножить на 4, 5, 8 или 16

0 4 Скоро в продаже
Шаг 1. Вы можете преобразовать эти задачи, чтобы они использовали только 2 и 10
Вот как:
- Чтобы умножить на 5, вместо этого умножьте на 10, а затем разделите на 2.
- Чтобы умножить на 4, вместо этого удвойте число, а затем снова удвойте.
- Для 8, 16, 32 или даже более высоких степеней двойки просто продолжайте удваивать. Например, 13 x 8 = 13 x 2 x 2 x 2, поэтому удвойте 13 три раза: 13 → 26 → 52 → 104.
Метод 8 из 12. Запомните трюк с 11-ю секундами
0 2 Скоро в продаже
Шаг 1. Вы можете умножить двузначное число на 11 практически без каких-либо математических операций
Сложите две цифры вместе, а затем поместите результат между исходными цифрами:
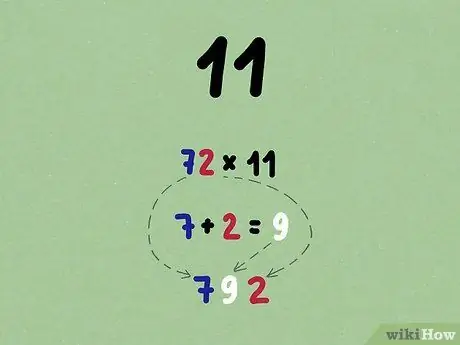
- Что 72 х 11?
- Сложите две цифры: 7 + 2 = 9.
- Поместите ответ между исходными цифрами: 72 x 11 = 792.
- Если сумма больше 10, поместите только последнюю цифру и перенесите единицу: 57 x 11 = 627, потому что 5 + 7 = 12. 2 идет посередине, а 1 добавляется к 5, чтобы получить 6.
Метод 9 из 12. Превратите проценты в более простые задачи
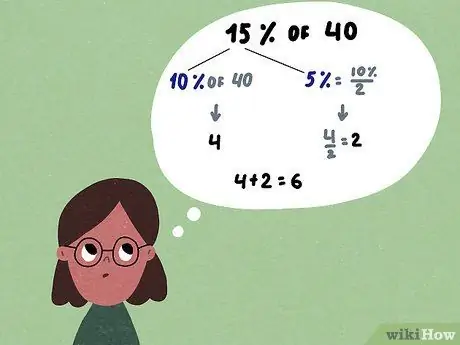
0 8 Скоро в продаже
Шаг 1. Знайте, какие проценты легче посчитать в уме
Есть пара полезных приемов, которые следует знать:
- 79% от 10 совпадает с 10% от 79. Это верно для любых двух чисел. Если вы не можете найти ответ на процентную проблему, попробуйте переключить его.
- Чтобы найти 10% числа, переместите десятичную дробь на одну позицию влево (10% от 65 равно 6,5). Чтобы найти 1% от числа, переместите десятичную запятую на два разряда влево (1% от 65 составляет 0,65).
-
Используйте эти правила для 10% и 1%, чтобы помочь вам с более сложными процентами. Например, 5% - это ½ от 10%, поэтому 5% от 80 = (10% от 80) x ½ = 8 x ½ =
Шаг 4..
- Разбейте проценты на более простые части: 30% от 900 = (10% от 900) x 3 = 90 x 3 = 270.
Метод 10 из 12. Запомните расширенные комбинации клавиш умножения для конкретных задач
0 3 Скоро в продаже
Шаг 1. Эти приемы мощные, но узкие
Они могут превратить кажущуюся невыполнимой задачу по математике в быстрое задание, но будут работать только с очень небольшим процентом задач. Изучите их, если вы уже достаточно хорошо разбираетесь в мысленной математике и хотите приблизиться к «математическим» уровням скорости:
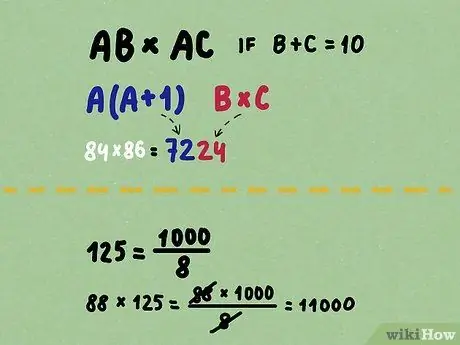
- Для таких проблем, как 84 х 86, где разряды десятков совпадают, а сумма цифр разряда единиц равна ровно 10, первые цифры ответа равны (8 + 1) x 8 = 72, а последние цифры - 4 x 6 = 24, для ответа 7224. То есть для задачи AB x AC, если B + C = 10, ответ начинается с A (A + 1) и заканчивается BC. Это также работает для больших чисел, если все цифры, кроме разряда единиц, идентичны.
- Вы можете переписать степени пяти (5, 25, 125, 625,…) как степени 10, разделенные на целое число (10/2, 100/4, 1000/8, 10000/16,…). Так 88 х 125 становится 88 x 1000 ÷ 8 = 88000 ÷ 8 = 11000.
Метод 11 из 12. Запомните диаграммы с квадратами

0 6 Скоро в продаже
Шаг 1. Графики квадратов дают вам новый способ умножения
Запоминание таблиц умножения от 1 до 9 делает автоматическое умножение однозначных чисел. Но для больших чисел, вместо того, чтобы пытаться запомнить сотни ответов, более эффективно запоминать только квадраты (каждое число умножается на себя). Немного поработав, вы можете использовать эти квадраты, чтобы найти ответ на другие проблемы:
- Запомните квадраты от 1 до 20 (или выше, если вы амбициозны). (То есть 1 x 1 = 1; 2 x 2 = 4; 3 x 3 = 9 и т. Д.)
- Чтобы умножить два числа, сначала найдите их среднее значение (число, которое находится точно между ними). Например, среднее значение 18 и 14 равняется 16.
- Возведите этот ответ в квадрат. После того, как вы запомните диаграмму квадратов, вы узнаете, что 16 x 16 равно 256.
- Затем посмотрите на разницу между исходными числами и их средним значением: 18-16 = 2. (Всегда используйте здесь положительное число).
- Также возведите это число в квадрат: 2 x 2 = 4.
- Чтобы получить окончательный ответ, возьмите первый квадрат и вычтите второй: 256 - 4 = 252.
Метод 12 из 12. Найдите полезные способы попрактиковаться в математической математике

0 1 Скоро в продаже
Шаг 1. Ежедневная практика имеет огромное значение
Если вы хотите повысить свою уверенность и скорость в мысленной математике, постарайтесь использовать эти навыки как минимум два или три раза в день. Эти предложения могут помочь вам сделать эту практику более эффективной:
- Карточки отлично подходят для запоминания таблиц умножения и деления или для того, чтобы привыкнуть к трюкам при решении конкретных задач. Напишите проблему с одной стороны, а ответ - с другой, и ежедневно задавайте себе вопросы, пока вы не разберетесь с ними.
- Онлайн-тесты по математике - еще один способ проверить свои способности. Поищите приложение или веб-сайт с хорошей репутацией, созданный в рамках образовательной программы.
- Практикуйтесь в повседневных ситуациях. Вы можете сложить общее количество товаров, которые вы покупаете в магазине, или умножить стоимость бензина за единицу на размер бака вашего автомобиля, чтобы найти общую стоимость. Чем больше это войдет в привычку, тем легче будет.
подсказки
- В реальном мире не всегда нужно знать точный ответ. Если вы находитесь в продуктовом магазине и пытаетесь сложить 7,07 + 8,95 + 10,09, вы можете округлить до ближайших целых чисел и оценить, что общая сумма составляет примерно 7 + 9 + 10 = 26.
- Некоторым людям легче мыслить деньгами, чем абстрактными числами. Вместо 100-55 попробуйте представить себе доллар минус монета 50 центов и монета 5 центов.
