В принципе, законы физики одинаковы и вперед, и назад. Но на практике время течет только в одном направлении.
Большинство законов физики одинаковы независимо от того, бежите вы часы вперед или назад. Планета, вращающаяся вокруг звезды, кажется, подчиняется тем же правилам, что и если бы вы записали ее и воспроизвели запись в обратном порядке. Это верно для любого гравитационного, электромагнитного или сильного ядерного взаимодействия между двумя частицами: они инвариантны к обращению времени. Обычно мы видим необратимые эффекты хаоса и термодинамики только с чрезвычайно большими системами, но в недавней статье утверждается, что это показано для гравитационного взаимодействия только с тремя массами. Джонатан Белью хочет знать, что это значит, спрашивая:
Имеет ли это какое-либо отношение к проблеме n тел, симметрии обращения времени в целом или последствиям для космологии? Или он теоретический и применим только к небольшому набору случаев, которые не составляют значительной части наблюдаемой Вселенной?
Давайте раскроем, что все это значит.
Хорошо известно, что почти все взаимодействия в физике подчиняются тому, что мы называем инвариантностью к обращению времени. Это означает, что законы физики ведут себя одинаково как в прямом, так и в обратном направлении. Вы можете просмотреть это несколькими способами, например:
- переведите часы вперед или назад во времени,
- запуская все частицы вашей системы с самого начала с их начальными импульсами или с конца с противоположными их конечными импульсами,
- или начиная с вашего конечного состояния и спрашивая, всегда ли есть способ развить это конечное состояние обратно в исходное состояние.
Для любой одной или двух частиц, подвергающихся какой-либо физической силе или взаимодействию, за исключением слабого ядерного взаимодействия (которое, как известно, нарушает симметрию обращения времени), всегда есть способ восстановить исходное состояние. если вы начинаете с вашего конечного состояния и развиваете его в соответствии с известными законами физики.

Однако макроскопический мир вовсе не кажется инвариантным к обращению времени. Конечно, если вы наблюдаете за мячом, летящим по воздуху, вверх или вниз по холму, за вращением Земли вокруг своей оси или за луной, вращающейся вокруг планеты, вы не сможете, просто взглянув на это, сказать, идут ли часы вперед или назад. Поскольку законы физики одинаковы в прямом и обратном направлении во времени - из-за этой инвариантности по отношению к обращению времени - одним и тем же правилам подчиняются.
Но другие явления явно имеют направление: стрела времени. Бросьте стакан воды на твердый пол и посмотрите, как он разобьется; реакция, обращенная во времени, никогда не произойдет, даже если вы проведете эксперимент квадриллионы раз. Яичница и повар и яйцо; яйцо никогда не «приготовится» и не «разложится». Это примеры того, что во Вселенной явно существует предпочтительное направление, то, что мы называем термодинамической стрелой времени.

Хотя в обоих этих случаях действуют только гравитационные и электромагнитные взаимодействия, взаимодействия становятся настолько сложными и происходят между таким количеством частиц - хаотически, помимо классически - , что в конечном итоге вы чрезвычайно маловероятно, что когда-либо вернется в исходное состояние, как бы хитро вы ни обращали реакцию.
Это как взять комнату с перегородкой посередине, где одна сторона горячая, а другая холодная, снять перегородку и наблюдать, как летают молекулы газа. В отсутствие каких-либо других входов две половины комнаты смешаются и уравновесятся, достигнув одинаковой температуры. Что бы вы ни делали с этими частицами, включая изменение всех их импульсов, они никогда больше не достигнут полугорячего или полухолодного состояния.
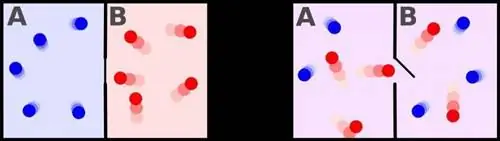
Этот тип необратимости хорошо изучен для больших систем со многими частицами и является неотъемлемой частью таких наук, как термодинамика и статистическая механика. Это одна из причин, почему мы так часто используем количество энтропии, и наше понимание этих процессов помогает нам понять второй закон термодинамики: в замкнутой системе энтропия только увеличивается или остается неизменной, никогда не уменьшаясь.
Но это понималось только в статистическом смысле. Только в системах с большим количеством частиц, взаимодействующих друг с другом, обычно проявляется этот тип хаоса, вызывая эти двойные явления необратимости времени и увеличения энтропии. Конечно, те же самые правила, которые управляют системами многих частиц, должны управлять и системами с небольшим количеством частиц, поэтому должны быть примеры хаоса, необратимости и увеличения энтропии в системах вообще без многих частиц.

В апрельском выпуске Ежемесячных уведомлений Королевского астрономического общества за 2020 год была опубликована новая статья под названием «Гигантские хаотические гравитационные системы из трех тел и их необратимость к планковской длине». (Полностью препринт доступен здесь.) Предыдущие исследования показали, что хаос является неотъемлемым свойством многих реальных астрофизических систем, в том числе:
- для небольших объектов с малой массой в Солнечной системе,
- системы с небольшим количеством звезд,
- отдельные звездные скопления,
- и галактики, которые эволюционируют со временем.
Если у вас есть небольшое, крошечное изменение в начальных условиях вашей системы - где только один объект находится в немного другом месте или имеет немного другую скорость - вы получите совершенно другой результат вниз дорога.
Если вы хотите понять, что такое увеличение энтропии, вам нужно обратить внимание на увеличение количества возможных исходов при старте с начальными условиями, которые лишь незначительно отличаются друг от друга. Иногда, если вы лишь немного измените начальные условия, вы получите одно и то же конечное состояние: это пример сходящегося решения, в котором энтропия существенно не увеличивается.
Но в других случаях вы столкнетесь с совершенно другими конечными состояниями: конечными состояниями, которые, по-видимому, имеют очень мало отношения к тому, с чего вы начали изначально. Это расходящиеся решения, и именно отсюда происходит увеличение энтропии. Хотя физические системы с большим количеством частиц могут прийти к этому, важно связать их физически с начальными условиями, с которых вы начинаете. Это труднее сделать для систем с большим количеством частиц, и последние несколько десятилетий это было спорной областью исследований.

Однако в последнее время достижения в области вычислительной мощности и алгоритмов грубой силы позволили решать некоторые очень простые задачи численно и определять такие вещи, как:
- какие задачи-и-условия сходятся, а какие расходятся,
- где все можно рассчитать с произвольной точностью (за счет времени вычислений),
- и где, если решение обратимо во времени, вы можете начать с конечного состояния и получить начальные условия с точностью до многих цифр для каждого тела в системе.
В новой работе Боекхольта, Портегиса Зварта и Валтонена была проанализирована система из трех невращающихся черных дыр одинаковой массы (то есть точечных масс), которые начинаются в состоянии покоя, но с произвольным позиции. Ранее было известно, что некоторые решения этой установки обратимы, в то время как другие считались необратимыми.
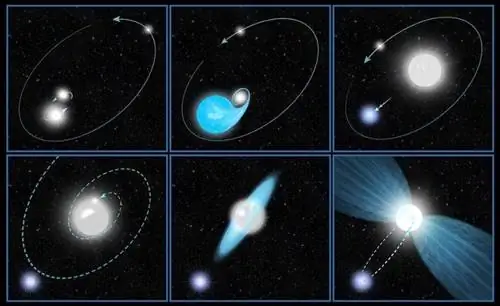
Эта новая работа действительно выводит наше понимание на новый уровень. По мере того, как вы повышаете точность своих расчетов, делая все меньшие и меньшие шаги и увеличивая свою числовую точность, все больше и больше решений, которые казались необратимыми, на самом деле оказывались обратимыми. Чем точнее (то есть, чем больше значащих цифр) вы рассчитали расстояние между любыми двумя объектами, тем лучше стала выглядеть обратимость во времени.
Но этому есть предел: предел, установленный квантовыми правилами, управляющими нашей Вселенной. Вы не можете вычислить расстояния с произвольной точностью в нашей физической реальности, потому что ниже определенной шкалы расстояний - планковской шкалы или около 10^-35 метров - законы физики нарушаются. Рассматривая черные дыры с массой ~1 миллион масс Солнца и начальным расстоянием порядка ~1 светового года, они обнаруживают, что около 5% всех конфигураций принципиально необратимы.
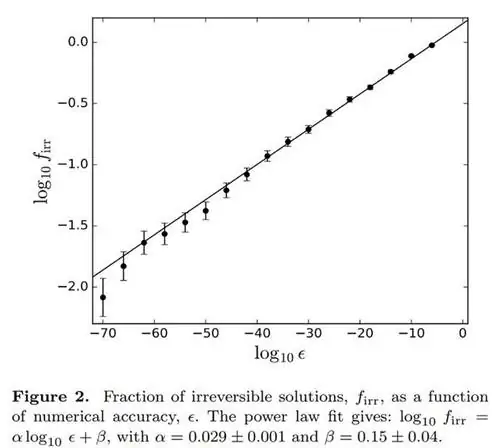
Это очень умный результат, чтобы узнать, что для реально больших объектов, которые мы имеем в нашей Вселенной, точность, необходимая для вычисления действительно обратимого во времени решения, больше, чем точность физической Вселенной на самом деле позволяет. Если законы квантовой физики и общей теории относительности верны, а у нас есть все основания полагать, что они верны, то даже чисто гравитационные системы с массой всего в три единицы фундаментально необратимы.
Конечно, многие другие реакции также известны как необратимые: две вращающиеся черные дыры испускают гравитационное излучение и инспиральное, но никакие вращающиеся черные дыры не поглощают гравитационное излучение и внеспиральное, например. Но впервые ученые продемонстрировали при условии, что законы физики таковы, как мы их себе представляем что чисто классическая система всего с тремя массами не всегда обратима во времени. Вселенная действительно непредсказуема и хаотична на фундаментальном уровне.
Отправляйте свои вопросы «Задайте Итану» по адресу startswithabang at gmail dot com!
