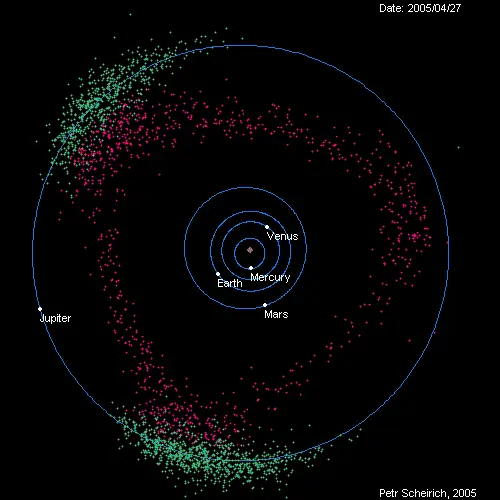
Если вы думали, что «планеты движутся вокруг Солнца по эллипсам», подождите, пока не прочитаете это.
«Я предпочитаю резкую критику одного разумного человека бездумному одобрению масс». - Иоганн Кеплер, 1601 г.
Когда дело доходит до вопросов и предложений, которые я получаю для «Спросите Итана», некоторые из них действительно глубоко погружаются в пределы науки и научных знаний. Наша цель как теоретика - создать модели, которые достаточно сложны, чтобы точно предсказывать все соответствующие явления в системе, и в то же время достаточно просты, чтобы мы могли их решить. Что ж, вопрос на этой неделе исходит от Алекса Б., редактора RealClearScience, который спрашивает следующее:
Указывает ли орбитальный распад (например, слияние двойных звезд) на то, что с законами Ньютона и Кеплера что-то не так? Помогает ли теория относительности объяснить это?
Вернемся к самому началу и дойдем до законов Ньютона и Кеплера.
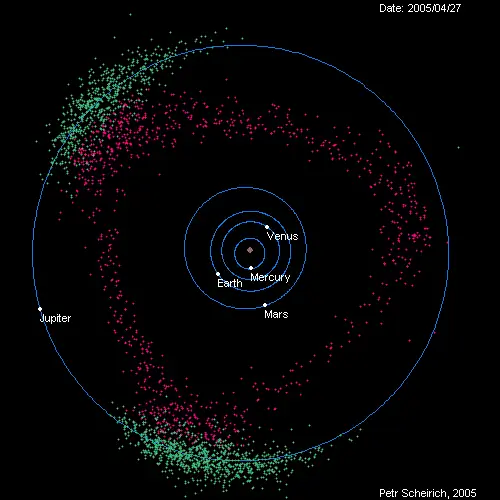
Рассматривая Солнце как фиксированную, стационарную точку в пространстве, мы могли бы отслеживать астрономическое движение всех небесных тел - планет, астероидов и комет - вокруг Солнца. Используя лучшие данные, доступные миру в то время (более 400 лет назад), Кеплер выяснил, что каждая из планет движется вовсе не по кругу с центром вокруг Солнца, а скорее по эллиптической траектории с Солнцем. в одном фокусе. Более полувека спустя Ньютон вычислил закон тяготения, благодаря которому эти орбиты произошли: универсальный закон тяготения Ньютона.
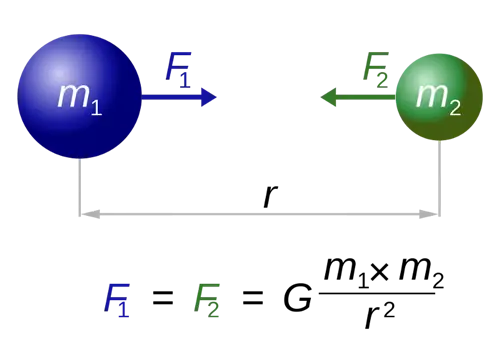
Теперь этот закон применим не только к планетам, вращающимся вокруг Солнца, или объектам в космосе, ни просто к падающим объектам здесь, на Земле. Нет, этот закон назвали «универсальным», потому что он в равной степени применим к любому объекту с массой во всей Вселенной.
Другими словами, если бы вы знали в любой момент времени местонахождение и массу всего, что есть во Вселенной, вы могли бы детерминистически предсказать, как все будет бесконечно развиваться под действием гравитации. далеко в будущее. Это полная сила закона Ньютона.

Но нам не нужно моделировать всю Вселенную, на самом деле это ужасная идея! Во-первых, потребуется компьютер такой же мощности, как вся Вселенная, чтобы запустить эту симуляцию с той же точностью, что и сама Вселенная. Что мы предпочитаем делать, а не вычислять эту силу индивидуально для всех субатомных точечных частиц во Вселенной и того, как они взаимодействуют друг с другом, так это делать простую модель.
А что, если мы возьмем очень простую систему: нашу Солнечную систему, состоящую только из планет и Солнца, и применим к ней законы Ньютона?

Вы можете подумать, что с этими девятью массами, разделенными огромными расстояниями, мы получим восемь эллипсов, движущихся вокруг неподвижного Солнца.
Ну, вот что вы получите, если сделаете следующий набор предположений:
- Все планеты и Солнце можно рассматривать как точечные массы.
- Орбита каждой планеты определяется только силой, с которой на нее действует Солнце. И наконец,
- Что законы Ньютона настолько абсолютны, что не существует таких вещей, как лоренц-инвариантность (или что законы физики не заботятся о том, как быстро вы движетесь, в данном конкретном случае).
На самом деле, конечно, все это неправда.

Планеты и Солнце вовсе не точечные. В то время как расстояния, отделяющие их друг от друга, очень велики по сравнению с их физическими размерами, их реальные размеры варьируются от гигантских (диаметр Меркурия 4 879 км) до колоссальных (диаметр Солнца 1 391 684 км). Все их массы распределены неравномерно, они более плотны в ядре и менее плотны по мере того, как мы движемся радиально наружу, и каждое тело в Солнечной системе вращается с некоторым ненулевым внутренним угловым моментом.
Держите в уме эту последнюю часть о вращении, когда мы движемся вперед; он нам снова понадобится через некоторое время.

Другие планеты имеют большое значение, особенно в течение длительных периодов времени, на орбитах друг друга! На самом деле ни одна из планет не образует идеальных эллипсов, а Солнце вовсе не неподвижно. Гравитационные силы, которые планеты воздействуют друг на друга, а также на Солнце, гарантируют, что эти орбиты вовсе не постоянны во времени, а скорее, что - если мы достаточно точны в наших расчетах и измерениях - мы должны быть в состоянии увидеть что орбитальные предсказания Кеплера - всего лишь приближение.
В действительности орбиты планет никогда не образуют замкнутый эллипс, и небольшое количество орбитальной энергии теряется с течением времени, поскольку учитываются даже более сложные явления, такие как столкновения с другими частицами.
Но это последний убийца, и впервые он был замечен еще до того, как теория относительности была разработана: Оливером Хевисайдом еще в 1893 году.

Допустим, у вас есть центральная масса, которая создает вокруг себя гравитационное поле. Кроме того, эта масса движется с некоторой скоростью (помните, что Солнце не стационарно), так что гравитационное поле со временем будет меняться. И, наконец, у вас есть еще одна массивная частица, движущаяся через это гравитационное поле. Ну и что будет?
Ничего не знать. Видите ли, примерно в то же время ученые рассматривали проблему того, что происходит, когда электрически заряженная частица движется через электрическое поле. В частности, они представляли атом как положительно заряженное ядро, вокруг которого вращается отрицательно заряженный электрон. Вы знаете, что там происходит?

Быстро движущаяся частица будет излучать электромагнитное излучение, несущее энергию. Следовательно, орбита со временем будет распадаться, а значит, материя должна быть нестабильной! Резерфорд открыл эту проблему для электромагнетизма, и она не была решена, пока десятилетия спустя не появилась квантовая механика.
Но в гравитации мы упираемся в пределы того, что могут предсказать законы Ньютона. Поскольку ньютоновской гравитации все равно, какова ваша скорость, она предсказывает, что не должно быть гравитационного излучения, когда вы ускоряетесь (то есть меняете свое направление) на орбите в гравитационном поле. Это недостаток теории, не являющейся лоренц-инвариантной. (Электромагнетизм, напротив, лоренц-инвариантен.)
Но так же, как существует электромагнетизм, должен существовать и гравитомагнетизм, если гравитация действительно лоренц-инвариантна. Возможно, вы слышали много шума вокруг Gravity Probe B, но, по правде говоря, уже существует более точное измерение гравитомагнетизма, которое уже некоторое время доступно.
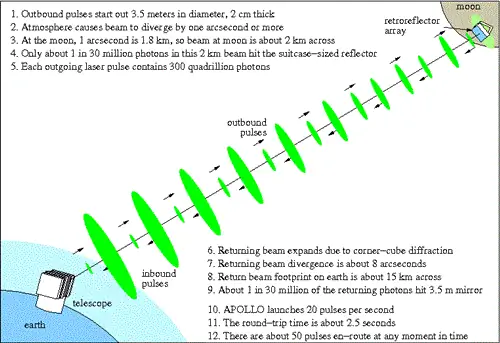
Измеряя точное положение Луны с помощью лазерной дальнометрии - чем мы занимаемся уже около 45 лет - мы смогли не только подтвердить эффект гравитомагнетизма (тот же самый эффект, ответственный за орбитальные), но обнаружить, что он согласуется с предсказаниями общей теории относительности с достоверностью 99,9% и неопределенностью 0,1%.
Для такой системы, как Земля, нашей планете потребуется 10^150 лет, чтобы повернуться к Солнцу по спирали, что намного дольше, чем время жизни нашей Солнечной системы. Но для такой системы, как двойной пульсар, она обречена всего через несколько сотен миллионов лет только из-за этого эффекта гравитационного излучения!
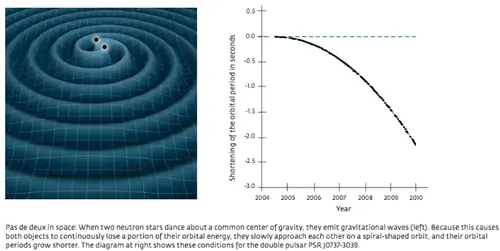
Таким образом, есть компонент законов Ньютона, который объясняет отклонение от замкнутых, идеальных эллипсов, когда речь идет об орбитах, но если вы хотите полностью объяснить наблюдаемые нами орбитальные распада, вам нужна теория, которая является инвариантом Лоренца - , который сохраняет законы физики одинаковыми независимо от вашей скорости - и общая теория относительности, даже после всех этих лет, по-прежнему работает лучше всех!
Так что спасибо за отличный вопрос, Алекс, и я надеюсь, что вы узнали что-то новое о гравитомагнетизме. Если у вас есть вопрос или предложение, которое вы хотели бы видеть в разделе «Спросите Итана», отправьте его, и следующее может быть вашим!
Оставляйте свои комментарии на форуме Starts With A Bang в блогах Scienceblogs.