Пифагор, возможно, считал, что весь космос был построен из прямоугольных треугольников.

Ключевые выводы
- Древние греки верили, что огонь, воздух, вода и земля являются четырьмя элементами вселенной.
- Платон связал эти четыре элемента с трехмерными геометрическими телами.
- Пифагор, возможно, считал, что прямоугольный треугольник лежит в основе всей реальности.
В диалоге Платона «Тимей» нам представлена теория о том, что космос состоит из прямоугольных треугольников.
Это предложение Тимей делает после того, как напомнил своей аудитории [49Bff], что более ранние теории, постулировавшие «воду» (предложенную Фалесом), или «воздух» (предложенную Анаксименом), или «огонь» (предложенную Гераклита) как изначальный материал, из которого был сотворен весь космос, натолкнулся на возражение: если наш мир полон этих расходящихся проявлений, как мы можем идентифицировать какой-либо из этих кандидатов в качестве основного материала? Ибо если есть огонь у плиты, жидкость в моей чашке, пригодный для дыхания невидимый воздух и храмы из твердого камня - а все они в основе своей представляют собой только один фундаментальный материал, - то как мы можем решить среди них, что является самым основным?
Космос геометрии
Однако, если основное основное единство, из которого состоит космос, оказывается прямоугольным треугольником, то предложение этой основной структуры, т. е. структуры огня, земли, воздуха и воды, может преодолеть это возражение. Вот что предлагает Тимей:
«Во-первых, для всякого, конечно, очевидно, что огонь, земля, вода и воздух суть тела; и все тела имеют объем. Кроме того, объем должен быть ограничен поверхностью, а всякая прямолинейная поверхность состоит из треугольников. Теперь все треугольники произошли от двух [то есть разносторонних и равнобедренных], каждый из которых имеет один прямой угол, а другие углы острые… Это мы предполагаем как первое начало огня и других тел, следуя объяснению, которое сочетает вероятность с необходимостью…» [Платон. Тимей 53Cff]
Чуть позже в этом диалоге Тимей предполагает, что из прямоугольных, разносторонних и равнобедренных треугольников построены элементы - мы могли бы назвать их молекулами. Если мы разместим на плоской поверхности равносторонние треугольники, равносторонние прямоугольники (т. Платоновые тела.
Сложатся три, четыре и пять равносторонних треугольников, а также три квадрата и три пятиугольника.

Если сумма фигур вокруг точки составляет четыре прямых угла или более, они не складываются. На данный момент я оставлю додекаэдр (или комбинацию трех пятиугольников, образующих «целое», в которое вписываются элементы), чтобы сосредоточиться на четырех элементах: тетраэдр (огонь), октаэдр (воздух), икосаэдр (вода)., и шестигранник (земля).
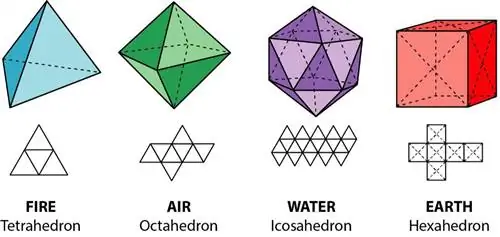
Все прямоугольный треугольник
Теперь, чтобы развить аргумент [53C], я предлагаю показать с помощью диаграмм, что прямоугольный треугольник является фундаментальной геометрической фигурой.
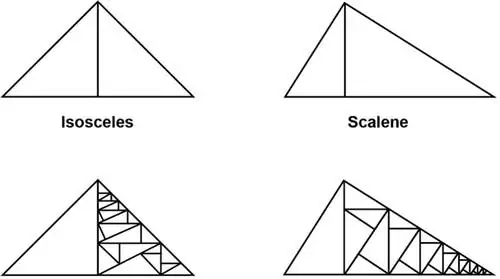
Все фигуры можно разрезать на треугольники. (Современным математикам это известно как мозаика или мозаика с треугольниками.)
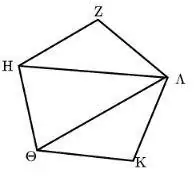
Внутри каждого вида треугольника - равностороннего, равнобедренного, разностороннего - есть два прямоугольных треугольника. Это можно увидеть, опустив перпендикуляр из вершины на противоположную сторону.
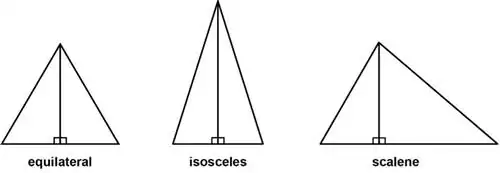
Внутри каждого прямоугольного треугольника - если делить из прямого угла - мы обнаружим два подобных прямоугольных треугольника, до бесконечности. Треугольники подобны, когда они имеют одинаковую форму, но разный размер.
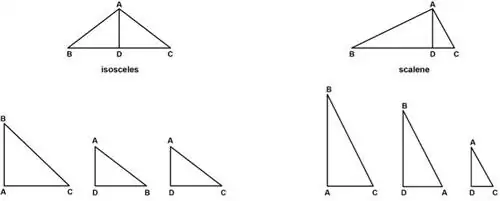
И таким образом, мы приходим к предположению Тимея, что прямоугольный треугольник является фундаментальной геометрической фигурой в двух ее видах, разносторонней и равнобедренной, которые содержат в себе бесконечное разделение на подобные прямоугольные треугольники.
Теперь никто не может предположить, что космос состоит из прямоугольных треугольников без доказательства - убедительной линии рассуждений - чтобы показать, что прямоугольный треугольник является фундаментальной геометрической фигурой. Тимей происходит из Локри, южной Италии, региона, куда эмигрировал Пифагор, а жили Эмпедокл и Алкмаон. Пифагорейцы, вероятно, являются источником вдохновения в этом отрывке, но не в двух других. Какое известное в то время доказательство показало, что это был прямоугольный треугольник? Могла ли это быть теорема Пифагора?
Теорема Пифагора выходит за рамки квадратов
Теперь мы знаем, что существует более 400 различных доказательств знаменитой теоремы. Доказывает ли один из них, что прямоугольный треугольник является основной геометрической фигурой? Будьте уверены, это не могло быть a² + b²=c², потому что это алгебра, а у греков алгебры не было! Более многообещающий источник - доказательство подобными прямоугольными треугольниками - это доказательство, сохранившееся в VI.31.
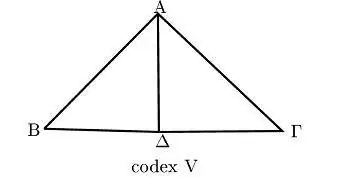
Обратите внимание, что на сторонах прямоугольного треугольника вообще нет фигур. (На приведенном выше рисунке прямой угол находится в точке «А».) Диаграмма показывает, что внутри каждого прямоугольного треугольника есть два подобных прямоугольных треугольника, разделенных навсегда.
Сегодня теорема Пифагора преподается с помощью квадратов.
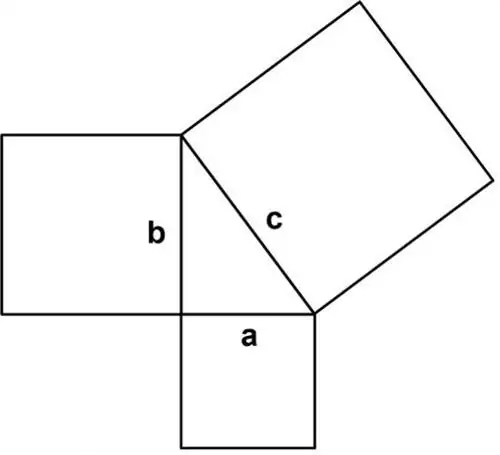
Но теорема Пифагора не имеет ничего общего с квадратами! Квадраты - это только частный случай. Теорема верна для всех фигур одинаковой формы и пропорционально нарисованных.

Итак, почему упор на квадраты? Потому что в древнегреческом мире пропорциональное масштабирование было трудно воспроизвести точно и трудно подтвердить, и подтверждение должно было прийти эмпирически. Но квадраты устраняют вопрос пропорционального масштабирования.
Пифагор и философия космологии
У нас есть древнее сообщение о том, что после своего доказательства Пифагор принес великое ритуальное жертвоприношение, возможно, сотню волов. Какое именно его открытие заслужило такой огромный жест?
Может ли этот обзор помочь нам начать понимать метафизический смысл теоремы о гипотенузе, а именно, то, что отмечалось, было не просто доказательством того, что площадь квадрата на гипотенузе прямоугольного треугольника был равен сумме площадей квадратов двух других сторон, но, кроме того, являлся ли доказательством того, что фундаментальной фигурой, из которой построен весь космос, был прямоугольный треугольник?
Проф. Роберт Хан интересуется историей древней и современной астрономии и физики, древними технологиями, вкладом Древнего Египта и монументальной архитектуры в раннегреческую философию и космологию, а также древней математикой и геометрией Египта и Греции. Каждый год он проводит выездные семинары «Древнее наследие» в Грецию, Турцию и Египет. Его последняя книга - «Метафизика теоремы Пифагора».
