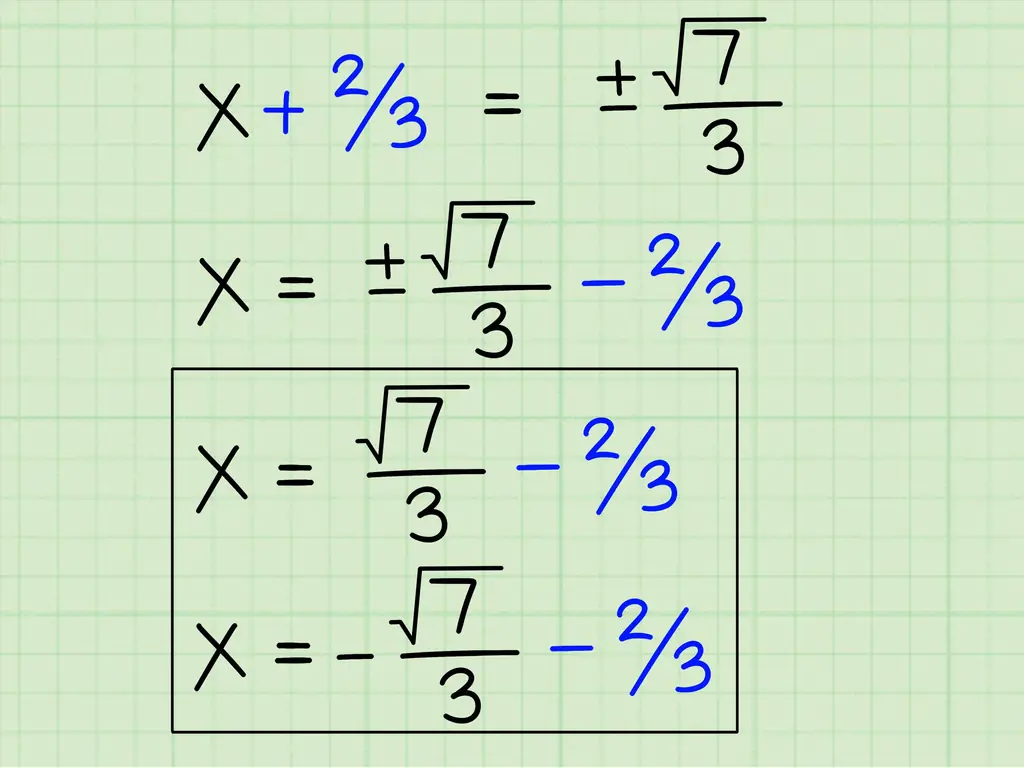Заполнение квадрата - полезный метод, который позволяет преобразовать квадратное уравнение в аккуратную форму, упрощающую визуализацию или даже решение. Вы можете заполнить квадрат, чтобы преобразовать более сложную квадратную формулу или даже решить квадратное уравнение. Если вы хотите знать, как это сделать, просто выполните следующие действия.
Шаги
Часть 1 из 2: преобразование стандартного уравнения в форму вершины
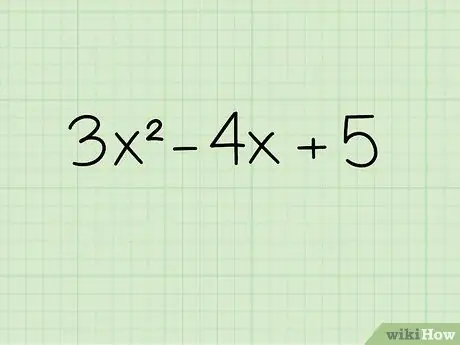
Шаг 1. Запишите уравнение
Допустим, вы работаете со следующим уравнением: 3x2 - 4х + 5.
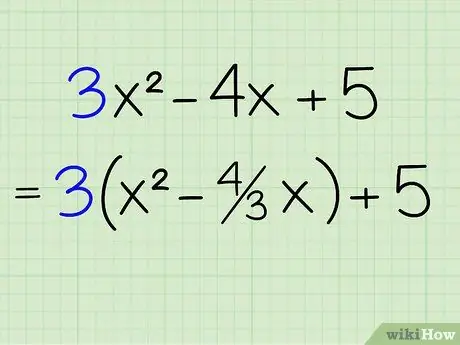
Шаг 2. Вычтите коэффициент при квадрате члена из первых двух членов
Чтобы вычленить тройку из первых двух членов, просто вытащите тройку и поместите ее в круглые скобки вокруг обоих терминов, разделив каждый член на 3. 3x2 делится на 3 - это просто x2 и 4x, разделенное на 3, будет 4 / 3x. Итак, новое уравнение должно выглядеть так: 3 (x2 - 4 / 3x) + 5. 5 останется за пределами уравнения, потому что вы не разделили его на 3.

Шаг 3. Разделите второй член пополам и возведите его в квадрат
Второй член, также известный как член b в уравнении, равен 4/3. Разделите второй член пополам или разделите его на 2 вначале. 4/3 ÷ 2 или 4/3 x 1/2 равно 2/3. Теперь возведите этот член в квадрат, возведя в квадрат числитель и знаменатель дроби. (2/3)2 = 4/9. Запишите этот термин.

Шаг 4. Добавьте и вычтите этот член из уравнения
Вам понадобится этот «дополнительный» член, чтобы превратить первые три члена в этом уравнении в полный квадрат. Но вы должны помнить, что вы добавили его, вычтя его из уравнения. Хотя очевидно, что простое объединение терминов не принесет вам особой пользы - вы вернетесь туда, откуда начали. Новое уравнение должно выглядеть так: 3 (x2 - 4/3 х + 4/9 - 4/9) + 5.

Шаг 5. Вытяните слово, которое вы вычли, из скобок
Поскольку вы работаете с коэффициентом 3 вне скобок, вы не можете просто вытащить -4/9. Сначала вам нужно умножить его на 3. -4/9 x 3 = -12/9 или -4/3. Если вы не работаете с уравнением с коэффициентом, отличным от 1 над x2 срок, то вы можете пропустить этот шаг.
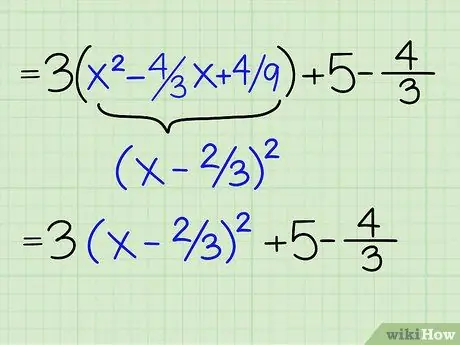
Шаг 6. Преобразуйте члены в круглых скобках в полный квадрат
Прямо сейчас у вас осталось 3 (x2 -4 / 3x +4/9) в скобках. Вы работали в обратном направлении, чтобы получить 4/9, что на самом деле было еще одним способом найти член, который завершит квадрат. Итак, вы можете переписать эти термины так: 3 (x - 2/3)2. Все, что вам нужно было сделать, это сократить вдвое второй срок и убрать третий. Вы можете проверить, работает ли это, умножив полученное значение, чтобы увидеть, что он дает вам первые три члена уравнения.
- 3 (х - 2/3)2 =
- 3 (х - 2/3) (х -2/3) =
- 3 [(x2 -2 / 3x -2 / 3x + 4/9)]
- 3 (х2 - 4 / 3x + 4/9)
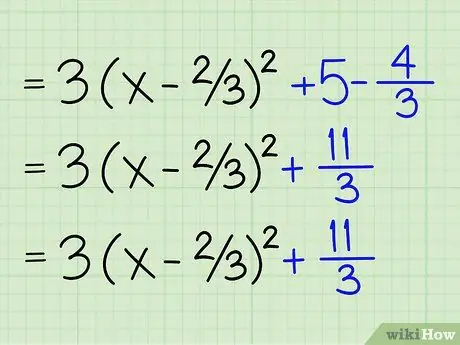
Шаг 7. Объедините постоянные члены
У вас остались два постоянных члена или термины, не привязанные к переменной. Прямо сейчас у вас осталось 3 (x - 2/3)2 - 4/3 + 5. Все, что вам нужно сделать, это сложить -4/3 и 5, чтобы получить 11/3. Вы делаете это, устанавливая для них один и тот же знаменатель: -4/3 и 15/3, а затем складывая числители, чтобы получить 11, и сохраняя знаменатель равным 3.
4/3 + 15/3 = 11/3
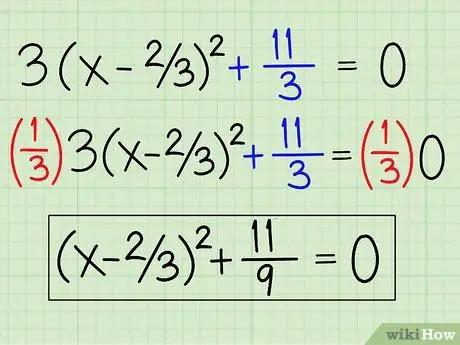
Шаг 8. Запишите уравнение в виде вершины
Все готово. Окончательное уравнение - 3 (x - 2/3).2 + 11/3. Вы можете удалить коэффициент 3, разделив обе части уравнения, чтобы получить (x - 2/3)2 + 11/9. Теперь вы успешно поместили уравнение в форму вершины, которая а (х - з)2 + к, где k представляет собой постоянный член.
Часть 2 из 2: Решение квадратного уравнения
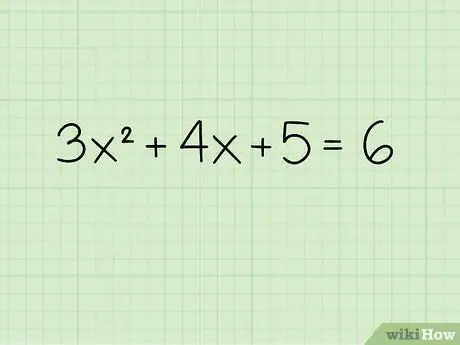
Шаг 1. Запишите проблему
Допустим, вы работаете со следующим уравнением: 3x2 + 4х + 5 = 6
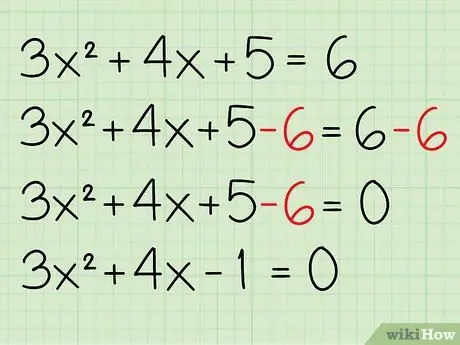
Шаг 2. Объедините постоянные члены и поместите их в левую часть уравнения
Постоянные термины - это любые термины, которые не привязаны к переменной. В этом случае у вас 5 слева и 6 справа. Вы хотите переместить 6 влево, поэтому вам придется вычесть 6 из обеих частей уравнения. В результате у вас останется 0 с правой стороны (6-6) и -1 с левой стороны (5-6). Теперь уравнение должно выглядеть так: 3x2 + 4х - 1 = 0.
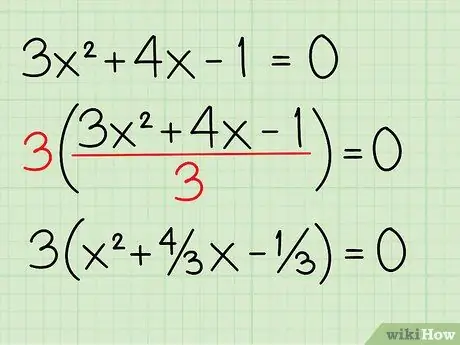
Шаг 3. Выносим за скобки коэффициент при квадрате члена
В данном случае 3 - коэффициент при x2 срок. Чтобы вынести 3, просто возьмите 3, заключите оставшиеся члены в скобки и разделите каждый член на 3. Итак, 3x2 ÷ 3 = х2, 4x ÷ 3 = 4 / 3x и 1 ÷ 3 = 1/3. Теперь уравнение должно выглядеть так: 3 (x2 + 4 / 3x - 1/3) = 0.
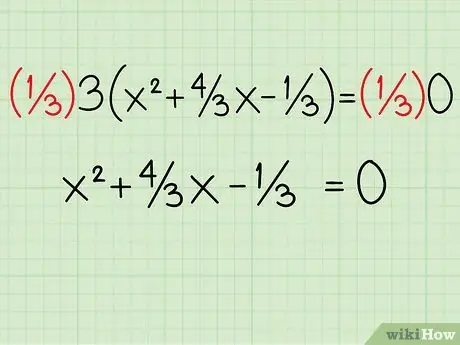
Шаг 4. Разделите на константу, которую вы только что исключили
Это означает, что вы можете навсегда избавиться от этого надоедливого термина 3 вне скобок. Поскольку вы разделили каждый член на 3, его можно удалить, не влияя на уравнение. Теперь у вас есть x2 + 4 / 3x - 1/3 = 0

Шаг 5. Разделите второй член пополам и возведите его в квадрат
Затем возьмите второй член, 4/3, также известный как член b, и найдите его половину. 4/3 ÷ 2 или 4/3 x 1/2, это 4/6 или 2/3. А 2/3 в квадрате - это 4/9. Когда вы закончите, вам нужно будет написать его слева и справа от уравнения, поскольку вы, по сути, добавляете новый член. Он понадобится вам с обеих сторон уравнения, чтобы он оставался сбалансированным. Теперь уравнение должно читаться как x2 + 4/3 х + 2/32 - 1/3 = 2/32
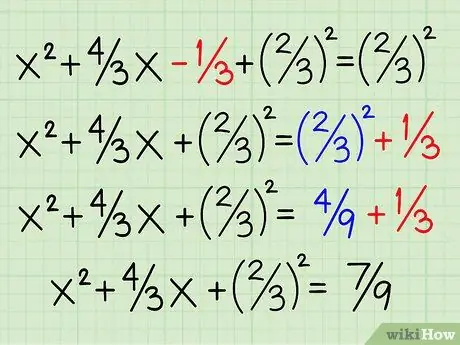
Шаг 6. Переместите исходный постоянный член в правую часть уравнения и добавьте его к члену с этой стороны
Переместите исходный постоянный член -1/3 вправо, чтобы сделать его 1/3. Добавьте его к слову, которое вы только что разместили, 4/9 или 2/3.2. Найдите общий знаменатель для объединения 1/3 и 4/9, умножив верхнюю и нижнюю части 1/3 на 3. 1/3 x 3/3 = 3/9. Теперь сложите 3/9 и 4/9, чтобы получить 7/9 в правой части уравнения. Это дает: x2 + 4/3 х + 2/32 = 4/9 + 1/3, а затем x2 + 4/3 х + 2/32 = 7/9.
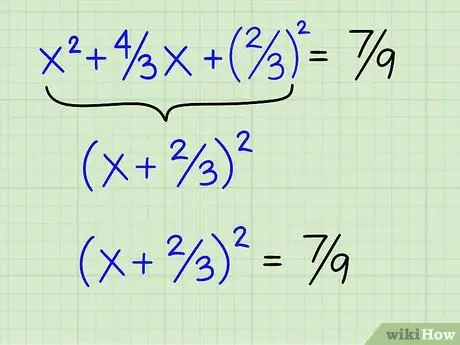
Шаг 7. Запишите левую часть уравнения в виде полного квадрата
Поскольку вы уже использовали формулу для поиска пропущенного члена, сложная часть уже позади. Все, что вам нужно сделать, это поместить x и половину второго коэффициента в круглые скобки и возвести их в квадрат, например: (x + 2/3)2. Обратите внимание, что разложение этого идеального квадрата даст вам три члена: x2 + 4/3 х + 4/9. Теперь уравнение должно выглядеть так: (x + 2/3)2 = 7/9.
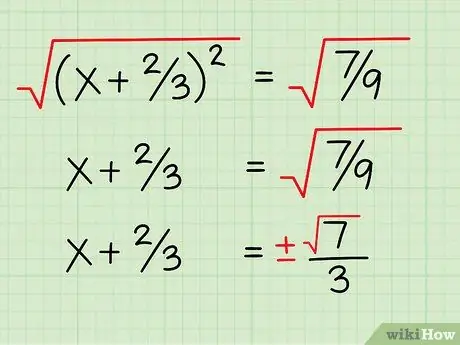
Шаг 8. Извлеките квадратный корень из обеих частей
В левой части уравнения квадратный корень из (x + 2/3)2 это просто x + 2/3. С правой стороны вы получите +/- (√7) / 3. Квадратный корень из знаменателя 9 равен четным 3, а квадратный корень из 7 равен √7. Не забудьте написать +/-, потому что квадратный корень может быть положительным или отрицательным.

Шаг 9. Изолируйте переменную
Чтобы изолировать переменную x, просто переместите постоянный член на 2/3 в правую часть уравнения. Теперь у вас есть два возможных ответа на x: ± (√7) / 3 - 2/3. Это два ваших ответа. Вы можете оставить это как есть или найти фактический квадратный корень из 7, если вам нужно дать ответ без знака радикала.
Видео - с помощью этой службы некоторая информация может быть передана YouTube
подсказки
- Даже после того, как вы знаете формулу квадратного уравнения, периодически практикуйтесь в завершении квадрата, доказывая формулу квадратного уравнения или выполняя некоторые практические задачи. Так вы не забудете, как это делать, когда вам это нужно.
- Обязательно поставьте ± в соответствующем месте, иначе вы получите только один ответ.