Это руководство предназначено для помощи тем, кому иногда приходится рассчитывать производные на курсах нематематического характера, таких как экономика, а также может быть использовано в качестве руководства для тех, кто только начинает изучать математический анализ. Это руководство предназначено для тех, кто уже знаком с алгеброй.
Примечание. В этом руководстве используется символ производной «», символ * используется для умножения, а ^ означает показатель степени.
Шаги
Часть 1 из 2: Начиная с основ
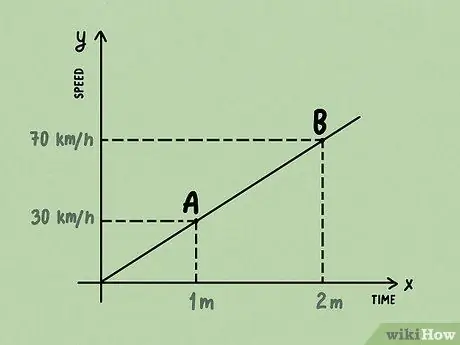
Шаг 1. Знайте, что производная - это вычисление скорости изменения функции
Например, если у вас есть функция, которая описывает, насколько быстро автомобиль движется из точки A в точку B, ее производная сообщит вам об ускорении автомобиля из точки A в точку B - насколько быстро или медленно изменяется скорость автомобиля.
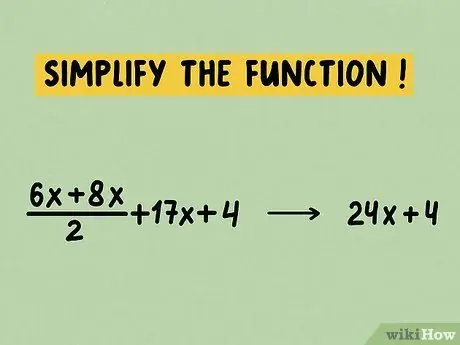
Шаг 2. Упростите функцию
Функции, которые не упрощены, по-прежнему будут давать ту же производную, но вычислить ее может быть намного сложнее.
-
Пример уравнения для упрощения:
- (6x + 8x) / 2 + 17x +4
- (14x) / 2 + 17x + 4
- 7x + 17x + 4
- 24x + 4

Шаг 3. Определите форму функции
Изучите различные формы.
- Просто число (например, 4)
- Число, умноженное на переменную без экспоненты (например, 4x)
- Число, умноженное на переменную с показателем степени (например, 4x ^ 2)
- Сложение (например, 4x + 4)
- Умножение переменных (например, вида x * x)
- Деление переменных (например, вида x / x)
Часть 2 из 2: Поиск производных различных форм

Шаг 1. Число:
Производная функции этого вида всегда равна нулю. Это потому, что в функции нет изменений - значение функции всегда будет числом, которое вам дано. Вот некоторые примеры:
- (4)' = 0
- (-234059)' = 0
- (пи) '= 0
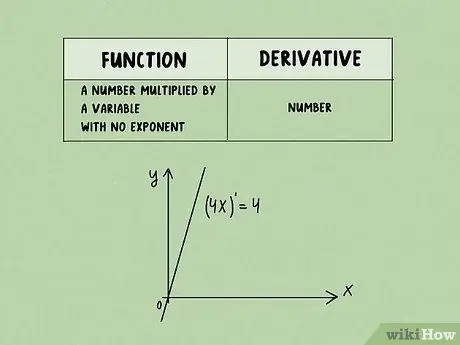
Шаг 2. Число, умноженное на переменную без экспоненты:
Производной функции этой формы всегда является число. Если x не имеет показателя степени, функция растет с постоянной, устойчивой, неизменной скоростью. Вы можете узнать этот трюк из линейного уравнения y = mx + b. Посмотрите эти примеры:
- (4x) '= 4
- (х) '= 1
- (-23x) '= -23

Шаг 3. Число, умноженное на переменную с показателем степени:
Вычтите единицу из экспоненты. Умножьте число на значение показателя степени. Например:
-
- (4x ^ 3) '= (4 * 3) (x ^ (3-1)) = 12x ^ 2
- (2x ^ 7) '= 14x ^ 6
- (3x ^ (- 1)) '= -3x ^ (- 2)

Шаг 4. Дополнение:
Возьмите производную каждой части выражения отдельно. Например:
- (4x + 4) '= 4 + 0 = 4
- ((х ^ 2) + 7x) '= 2x + 7

Шаг 5. Умножение переменных:
Умножьте первую переменную на производную второй переменной. Умножьте вторую переменную на производную первой переменной. Сложите два результата вместе. Вот пример:
((x ^ 2) * x) '= (x ^ 2) * 1 + x * 2x = (x ^ 2) + 2x * x = 3x ^ 2

Шаг 6. Разделение переменных:
Умножьте нижнюю переменную на производную верхней переменной. Умножьте верхнюю переменную на производную нижней переменной. Вычтите результат на шаге 2 из результата на шаге 1. Будьте осторожны, упорядочивайте материалы! Разделите результат на шаге 3 квадратом нижней переменной. Посмотрите этот пример:
-
((x ^ 7) / x) '= (7x ^ 6 * x - 1 * x ^ 7) / (x ^ 2) = (7x ^ 7 - x ^ 7) / (x ^ 2) = 6x ^ 7 / х ^ 2 = 6х ^ 5
Это, пожалуй, самый сложный трюк, но он того стоит. Убедитесь, что вы выполняете шаги по порядку и вычитаете в правильном порядке, и все пройдет гладко
