Чтобы сложить и вычесть квадратные корни, вам нужно объединить квадратные корни с одним и тем же радикальным членом. Это означает, что вы добавляете или вычитаете 2√3 и 4√3, но не 2√3 и 2√5. Есть много случаев, когда вы действительно можете упростить число внутри радикала, чтобы иметь возможность комбинировать одинаковые термины и свободно складывать и вычитать квадратные корни.
Шаги
Часть 1 из 2: основные сведения
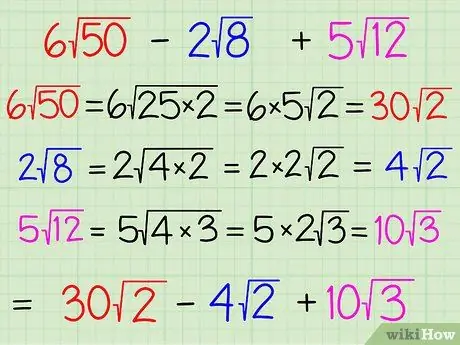
Шаг 1. По возможности упрощайте любые термины внутри радикалов
Чтобы упростить термины внутри радикалов, попробуйте разложить их на множители, чтобы найти хотя бы один член, представляющий собой полный квадрат, например 25 (5 x 5) или 9 (3 x 3). Как только вы это сделаете, вы можете извлечь квадратный корень из идеального квадрата и записать его вне радикала, оставив оставшийся множитель внутри радикала. В этом примере мы работаем с задачей 6√50 - 2√8 + 5√12. Цифры вне знака корня - это коэффициенты, а числа внутри него - подкоренные. Вот как можно упростить каждый из терминов:
- 6√50 = 6√ (25 x 2) = (6 x 5) √2 = 30√2. Здесь вы разложили «50» на «25 x 2», а затем вытащили «5» из идеального квадрата «25» и поместили его вне корня, а «2» осталась внутри.. Затем вы умножили «5» на «6», число, которое уже находится вне радикала, чтобы получить 30 в качестве нового коэффициента.
- 2√8 = 2√ (4 x 2) = (2 x 2) √2 = 4√2. Здесь вы разложили «8» на «4 x 2», а затем вытащили «2» из идеального квадрата «4» и поместили его вне корня, оставив «2» внутри. Затем вы умножили «2» на «2», число, которое уже находится вне корня, чтобы получить 4 в качестве нового коэффициента.
- 5√12 = 5√ (4 x 3) = (5 x 2) √3 = 10√3. Здесь вы разложили «12» на «4 x 3» и вытащили «2» из идеального квадрата «4» и поместили его вне корня, оставив множитель «3» внутри. Затем вы умножили «2» на «5», число, которое уже находится вне корня, чтобы получить 10 в качестве нового коэффициента.

Шаг 2. Обведите любые термины с соответствующими подкоренными элементами
После того как вы упростили подкоренные выражения в данных вам терминах, у вас осталось следующее уравнение: 30√2 - 4√2 + 10√3. Поскольку вы можете складывать или вычитать только одинаковые термины, вам следует обвести в кружки термины с одинаковым радикалом, которые в этом примере равны 30√2 и 4√2. Вы можете думать об этом как о сложении или вычитании дробей, когда вы можете складывать или вычитать только те члены, если знаменатели совпадают.

Шаг 3. Если вы работаете с более длинным уравнением и есть несколько пар с совпадающими подкоренными выражениями, вы можете обвести первую пару, подчеркнуть вторую, поставить звездочку возле третьей и так далее
Выстраивание терминов по порядку также облегчит вам визуализацию решения.
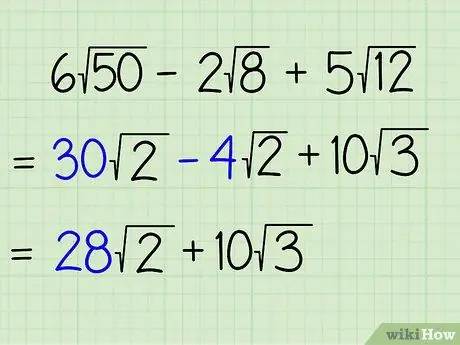
Шаг 4. Сложите или вычтите коэффициенты членов с совпадающими подкоренными выражениями
Теперь все, что вам нужно сделать, это добавить или вычесть коэффициенты членов с соответствующими подкоренными выражениями и оставить любые дополнительные члены как часть уравнения. Не смешивайте подкоренные вещества. Идея состоит в том, что вы говорите, сколько всего есть подкоренного типа этого типа. Несовпадающие термины могут оставаться как есть. Вот что вы делаете:
- 30√2 - 4√2 + 10√3 =
- (30 - 4)√2 + 10√3 =
- 26√2 + 10√3
Часть 2 из 2: больше практики

Шаг 1. Проделайте Пример 1
В этом примере вы складываете следующие квадратные корни: √ (45) + 4√5. Вот что вам нужно сделать:
- Упростим √ (45). Во-первых, вы можете разложить его на множители, чтобы получить √ (9 x 5).
- Затем вы можете вытащить «3» из идеального квадрата «9» и сделать его коэффициентом при радикале. Итак, √ (45) = 3√5.
- Теперь просто сложите коэффициенты двух членов с соответствующими подкоренными выражениями, чтобы получить ответ. 3√5 + 4√5 = 7√5

Шаг 2. Проделайте Пример 2
Этот пример представляет собой следующую задачу: 6√ (40) - 3√ (10) + √5. Вот что вам нужно сделать, чтобы решить эту проблему:
- Упростим 6√ (40). Сначала вы можете вынести «40», чтобы получить «4 x 10», что составляет 6√ (40) = 6√ (4 x 10).
- Затем вы можете вытащить «2» из идеального квадрата «4», а затем умножить его на текущий коэффициент. Теперь у вас есть 6√ (4 x 10) = (6 x 2) √10.
- Умножьте два коэффициента, чтобы получить 12√10.
- Теперь ваша задача выглядит так: 12√10 - 3√ (10) + √5. Поскольку первые два члена имеют одно и то же подкоренное выражение, вы можете вычесть второй член из первого и оставить третий как есть.
- У вас осталось (12-3) √10 + √5, которое можно упростить до 9√10 + √5.

Шаг 3. Проделайте Пример 3
Этот пример следующий: 9√5 -2√3 - 4√5. Здесь ни один из радикалов не имеет множителей, являющихся полными квадратами, поэтому упрощение невозможно. Первый и третий члены подобны радикалам, поэтому их коэффициенты уже можно комбинировать (9 - 4). Подкормка не затрагивается. Остальные члены не похожи, поэтому задачу можно упростить до 5√5 - 2√3.

Шаг 4. Проделайте Пример 4
Допустим, вы работаете со следующей задачей: √9 + √4 - 3√2. Вот что ты делаешь:
- Поскольку √9 равно √ (3 x 3), вы можете упростить √9 до 3.
- Поскольку √4 равно √ (2 x 2), вы можете упростить √4 до 2.
- Теперь вы можете просто сложить 3 + 2, чтобы получить 5.
- Поскольку 5 и 3√2 не похожи на термины, вы больше ничего не можете сделать. Ваш окончательный ответ 5 - 3√2.
Шаг 5. Проделайте Пример 5
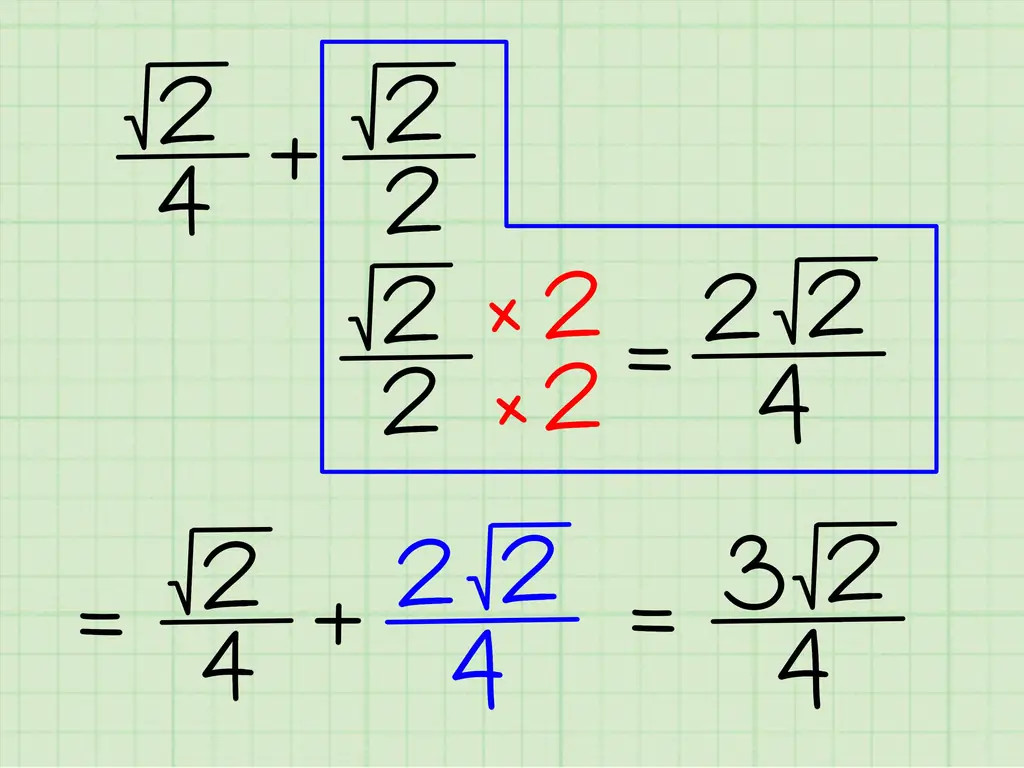
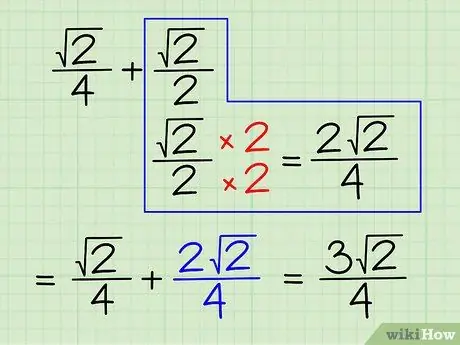
Давайте попробуем сложить и вычесть квадратные корни, являющиеся частью дроби. Теперь, как и в случае с обычной дробью, вы можете складывать или вычитать только дроби с одинаковым числителем или знаменателем. Допустим, вы работаете с этой проблемой: (√2) / 4 + (√2) / 2. Вот что вы делаете:
- Сделайте так, чтобы у этих терминов был одинаковый знаменатель. Наименьший общий знаменатель или знаменатель, который делился бы без остатка на оба знаменателя «4» и «2», равен «4».
- Итак, чтобы второй член (√2) / 2 имел знаменатель 4, вам нужно умножить его числитель и знаменатель на 2/2. (√2) / 2 х 2/2 = (2√2) / 4.
- Сложите числители дробей, оставив знаменатель прежним. Делайте то же, что и при добавлении дробей. (√2) / 4 + (2√2) / 4 = 3√2) / 4.
Видео - с помощью этой службы некоторая информация может быть передана YouTube
подсказки
Всегда упрощайте любые подкоренные выражения с точными квадратными множителями до вы начинаете идентифицировать и комбинировать как подкоренные.
Предупреждения
- Никогда не комбинируйте непохожие радикалы.
-
Никогда не объединяйте целое число и радикал так, чтобы это означало, что: 3 + (2x)1/2 жестяная банка нет быть упрощенным.
Примечание: произнося "половина мощности (2x)" = (2x)1/2 это просто еще один способ сказать "квадратный корень из (2x)".