Как сделать неявную дифференциацию: 7 шагов (с изображениями)

В исчислении, когда у вас есть уравнение для y, записанное через x (например, y = x² -3x), для нахождения производной легко использовать базовые методы дифференцирования (известные математикам как методы «явного дифференцирования»). Однако для уравнений, которые сложно переставить, если y стоит по одну сторону от знака равенства (например, x² + y² - 5x + 8y + 2xy² = 19), нужен другой подход. С помощью техники, называемой неявным дифференцированием, легко найти производные уравнений с несколькими переменными, если вы уже знаете основы явного дифференцирования!

Шаги

Метод 1 из 2: быстрое определение простых уравнений

Выполните неявное дифференцирование, шаг 1

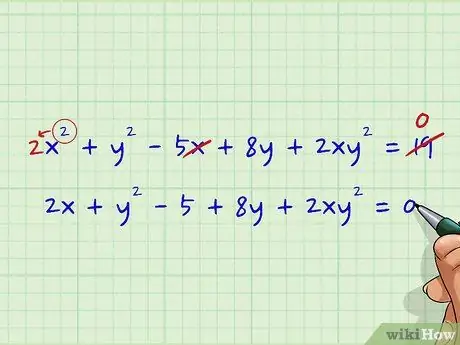
Шаг 1. Дифференцируйте члены x как обычно

При попытке дифференцировать многомерное уравнение, такое как x² + y² - 5x + 8y + 2xy² = 19, может быть трудно понять, с чего начать. К счастью, первый шаг неявной дифференциации - самый простой. Для начала просто дифференцируйте члены x и константы с обеих сторон уравнения в соответствии с обычными (явными) правилами дифференцирования. Игнорируйте пока термины y.

Давайте попробуем дифференцировать простой пример уравнения, приведенный выше. Икс² + y² - 5x + 8y + 2xy² = 19 имеет два члена x: x² и -5x. Если мы хотим дифференцировать уравнение, сначала разберемся с ними, например:

Икс² + y² - 5x + 8y + 2xy² = 19

(Приведите показатель "2" в x² вниз в качестве коэффициента, удалите x в -5x и измените 19 на 0)

2x + y² - 5 + 8л + 2кс² = 0

Шаг 2. Разделите y-члены и добавьте «(dy / dx)» рядом с каждым

В качестве следующего шага просто дифференцируйте члены y так же, как вы дифференцировали члены x. Однако на этот раз добавьте «(dy / dx)» рядом с каждым так же, как если бы вы добавляли коэффициент. Например, если вы дифференцируете y², он становится 2y (dy / dx). Пока не обращайте внимания на термины с x и y.

В нашем текущем примере уравнение теперь выглядит так: 2x + y² - 5 + 8л + 2кс² = 0. Мы бы выполнили следующий шаг дифференцирования по оси y следующим образом:

2x + y² - 5 + 8л + 2кс² = 0

(Приведите показатель степени "2" в y² вниз в качестве коэффициента, удалите y из 8y и поместите «dy / dx» рядом с каждым).

2x + 2y (dy / dx) - 5 + 8 (dy / dx) + 2xy²= 0

Выполните неявное дифференцирование, шаг 3

Шаг 3. Используйте правило произведения или правило частного для членов с x и y

Работать с терминами, в которых есть как x, так и y, немного сложно, но если вы знаете правила дифференциации продукта и частного, то вам все ясно. Если члены x и y умножаются, используйте правило произведения ((f × g) '= f' × g + g '× f), подставив член x вместо f и член y вместо g. С другой стороны, если члены x и y делятся друг на друга, используйте правило частного ((f / g) '= (g × f' - g '× f) / g²), заменив числитель вместо f и знаменатель для g.

В нашем примере 2x + 2y (dy / dx) - 5 + 8 (dy / dx) + 2xy² = 0, у нас есть только один член с x и y - 2xy². Поскольку x и y умножаются друг на друга, мы будем использовать правило произведения, чтобы различать следующее:

2xy² = (2x) (y²) - положим 2x = f и y² = g в (f × g) '= f' × g + g '× f

(f × g) '= (2x)' × (y²) + (2x) × (y²)'

(f × g) '= (2) × (y²) + (2x) × (2y (dy / dx))

(f × g) '= 2 года² + 4xy (dy / dx)
Добавляя это обратно в наше основное уравнение, мы получаем 2x + 2y (dy / dx) - 5 + 8 (dy / dx) + 2y² + 4xy (dy / dx) = 0

Выполните неявное дифференцирование, шаг 4

Шаг 4. Изолируйте (dy / dx)

Ты почти там! Теперь все, что вам нужно сделать, это решить уравнение для (dy / dx). Это выглядит сложно, но обычно это не так - имейте в виду, что любые два члена a и b, умноженные на (dy / dx), могут быть записаны как (a + b) (dy / dx) из-за распределительного свойства умножения. Эта тактика может упростить выделение (dy / dx) - просто возьмите все остальные термины на противоположной стороне круглых скобок, а затем разделите их на термины в скобках рядом с (dy / dx).

В нашем примере мы могли бы упростить 2x + 2y (dy / dx) - 5 + 8 (dy / dx) + 2y² + 4xy (dy / dx) = 0 следующим образом:

2x + 2y (dy / dx) - 5 + 8 (dy / dx) + 2y² + 4xy (dy / dx) = 0

(2y + 8 + 4xy) (dy / dx) + 2x - 5 + 2y² = 0

(2y + 8 + 4xy) (dy / dx) = -2y² - 2x + 5

(dy / dx) = (-2y² - 2x + 5) / (2y + 8 + 4xy)

(dy / dx) = (-2y² - 2x + 5) / (2 (2xy + y + 4)

Метод 2 из 2: Использование продвинутых методов

Выполните неявное дифференцирование, шаг 5

Шаг 1. Подставьте значения (x, y), чтобы найти (dy / dx) для любой точки

Поздравляю! Вы неявно дифференцировали свое уравнение - непростая задача для новичков! Использовать это уравнение для определения наклона (dy / dx) для любой точки (x, y) так же просто, как вставить значения x и y для вашей точки в правую часть уравнения, а затем решить для (dy / dx).

Например, предположим, что мы хотим найти наклон в точке (3, -4) для нашего примера уравнения выше. Для этого мы заменим 3 на x и -4 на y, решив следующее:

(dy / dx) = (-2y² - 2x + 5) / (2 (2xy + y + 4)

(dy / dx) = (-2 (-4)² - 2(3) + 5)/(2(2(3)(-4) + (-4) + 4)

(dy / dx) = (-2 (16) - 6 + 5) / (2 (2 (3) (- 4))

(dy / dx) = (-32) - 6 + 5) / (2 (2 (-12))

(dy / dx) = (-33) / (2 (2 (-12))

(dy / dx) = (-33) / (- 48) = 3/48, или 0.6875.

Выполните неявное дифференцирование, шаг 6

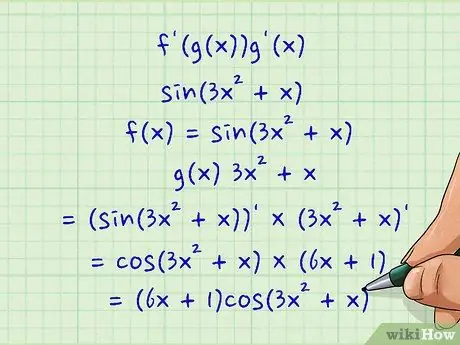
Шаг 2. Используйте правило цепочки для функций внутри функций

Цепное правило - важная часть знаний, которую нужно иметь при работе с задачами исчисления (включая проблемы неявного дифференцирования). Цепное правило гласит, что для функции F (x), которую можно записать как (f о g) (x) производная F (x) равна f '(g (x)) g' (x). Для сложных задач неявного дифференцирования это означает, что можно дифференцировать различные отдельные «части» уравнения, а затем сложить результат.

В качестве простого примера предположим, что нам нужно найти производную sin (3x² + x) как часть более крупной задачи неявного дифференцирования для уравнения sin (3x² + х) + у³ = 0. Если мы подумаем о грехе (3x² + x) как "f (x)" и 3x² + x как "g (x)", мы можем найти дифференцирование следующим образом:

f '(g (x)) g' (x)

(грех (3x² + x)) '× (3x² + х) '

cos (3x² + х) × (6х + 1)

(6x + 1) cos (3x² + х)

Выполните неявное дифференцирование, шаг 7

Шаг 3. Для уравнений с переменными x, y и z найдите (dz / dx) и (dz / dy)

Хотя это не распространено в базовом исчислении, в некоторых сложных приложениях может потребоваться неявное дифференцирование более двух переменных. Для каждой дополнительной переменной вам нужно будет найти дополнительную производную по x. Например, если вы работаете с x, y и z, вам нужно найти и (dz / dy), и (dz / dx). Мы можем сделать это, дважды дифференцируя уравнение по x: в первый раз мы будем вставлять (dz / dx) каждый раз, когда мы дифференцируем член с помощью z, а во второй раз мы вставим (dz / dy) каждый раз, когда мы дифференцируем z. После этого остается только решить для (dz / dx) и (dz / dy).

Например, предположим, что мы пытаемся различить x³z² - 5xy⁵г = х² + y³.
Во-первых, давайте дифференцируем по x и вставим (dz / dx). Не забудьте применить правило продукта там, где это необходимо!

Икс³z² - 5xy⁵г = х² + y³

3x²z² + 2x³z (dz / dx) - 5 лет⁵z - 5xy⁵(dz / dx) = 2x

3x²z² + (2x³z - 5xy⁵) (dz / dx) - 5 лет⁵z = 2x

(2x³z - 5xy⁵) (dz / dx) = 2x - 3x²z² + 5лет⁵z

(dz / dx) = (2x - 3x²z² + 5лет⁵z) / (2x³z - 5xy⁵)
Теперь сделаем то же самое для (dz / dy)

Икс³z² - 5xy⁵г = х² + y³

2x³z (dz / dy) - 25xy⁴z - 5xy⁵(dz / dy) = 3y²

(2x³z - 5xy⁵) (dz / dy) = 3y² + 25xy⁴z

(dz / dy) = (3y² + 25xy⁴z) / (2x³z - 5xy⁵)