Как разложить на множители: 11 шагов (с картинками)

Факторы числа - это числа, которые умножаются вместе, чтобы сформировать его как произведение. Другой способ мышления заключается в том, что каждое число является продуктом нескольких факторов. Умение факторизовать, то есть разбивать число на составляющие факторы, - это важный математический навык, который используется не только в базовой арифметике, но также в алгебре, исчислении и не только. См. Шаг 1 ниже, чтобы научиться учитывать фактор!

Шаги

Метод 1 из 2: факторинг основных целых чисел

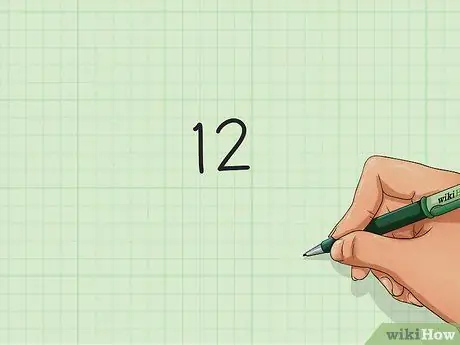
Шаг 1. Напишите свой номер

Чтобы начать факторинг, все, что вам нужно, это число - подойдет любое число, но для наших целей давайте начнем с простого целого числа. Целые числа - это числа без дробных или десятичных компонентов (все положительные и отрицательные целые числа являются целыми числами).

• Выберем номер

  Шаг 12.. Запишите это число на листе бумаги для заметок.

Шаг 2. Найдите еще два числа, из которых получится первое число

Любое целое число можно записать как произведение двух других целых чисел. Даже простые числа можно записать как произведение 1 и самого числа. Думая о числе как о произведении двух факторов, может потребоваться «обратное» мышление - по сути, вы должны спросить себя: «Какая задача умножения равна этому числу?»

• В нашем примере 12 имеет несколько множителей - 12 × 1, 6 × 2 и 3 × 4, все равны 12. Итак, мы можем сказать, что множители 12 равны 1, 2, 3, 4, 6 и 12. Для наших целей будем работать с факторами 6 и 2.
• Четные числа особенно легко разложить на множители, потому что каждое четное число имеет множитель 2. 4 = 2 × 2, 26 = 13 × 2 и т. Д.

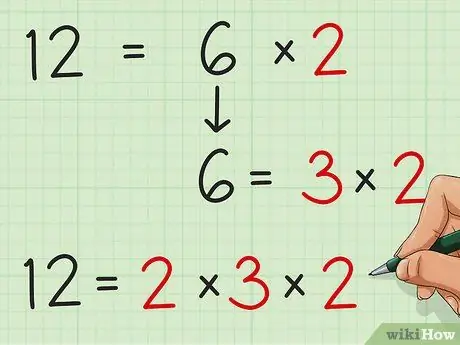
Шаг 3. Определите, можно ли еще раз учесть какие-либо из ваших факторов

Многие числа, особенно большие, можно разложить на множители. Когда вы нашли два из числа факторов, если у одного есть свой собственный набор факторов, вы также можете уменьшить это число до его факторов. В зависимости от ситуации это может быть полезно, а может и нет.

Например, в нашем примере мы уменьшили 12 до 2 × 6. Обратите внимание, что 6 имеет свои собственные множители - 3 × 2 = 6. Таким образом, мы можем сказать, что 12 = 2 × (3 × 2).

Шаг 4. Прекратите факторинг при достижении простых чисел

Простые числа - это числа больше 1, которые делятся без остатка только сами по себе и 1. Например, 2, 3, 5, 7, 11, 13 и 17 являются простыми числами. Когда вы разложили на множители число так, что оно является произведением исключительно простых чисел, дальнейшее разложение на множители излишне. Нет смысла сводить каждый фактор к самому себе, умноженному на единицу, так что можете остановиться.

В нашем примере мы уменьшили 12 до 2 × (2 × 3). 2, 2 и 3 - все простые числа. Если бы мы использовали дополнительные факторы, нам пришлось бы разложить на множители (2 × 1) × ((2 × 1) (3 × 1)), что обычно бесполезно, поэтому его обычно избегают

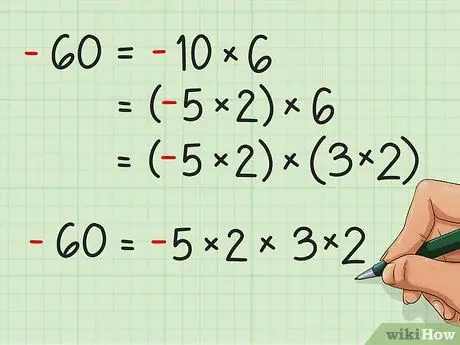
Шаг 5. Таким же образом разложите на множители отрицательные числа

Факторизация отрицательных чисел практически идентична факторизации положительных чисел. Единственное отличие состоит в том, что факторы должны умножаться вместе, чтобы получить отрицательное число в качестве их произведения, поэтому нечетное количество факторов должно быть отрицательным.

• Например, множим -60. См. ниже:

  • -60 = -10 × 6
  • -60 = (-5 × 2) × 6
  • -60 = (-5 × 2) × (3 × 2)
  • -60 = - 5 × 2 × 3 × 2. Обратите внимание, что наличие нечетного числа отрицательных чисел, кроме одного, даст тот же продукт. Например, - 5 × 2 × -3 × -2 также равно 60.

Метод 2 из 2: стратегия факторинга больших чисел

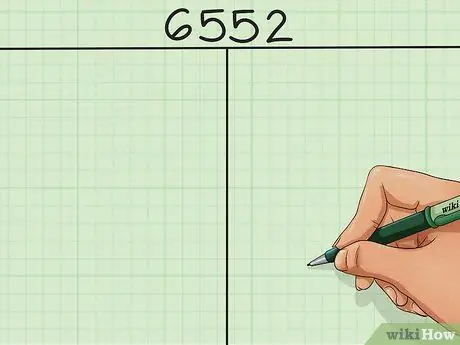
Шаг 1. Напишите свой номер над таблицей из 2 столбцов

Хотя обычно небольшие целые числа довольно легко разложить на множители, большие числа могут быть пугающими. Большинству из нас было бы трудно разбить четырех- или пятизначное число на простые множители, используя только мысленную математику. К счастью, с помощью таблицы процесс становится намного проще. Напишите свой номер над таблицей в форме буквы Т с двумя столбцами - вы будете использовать эту таблицу для отслеживания растущего списка факторов.

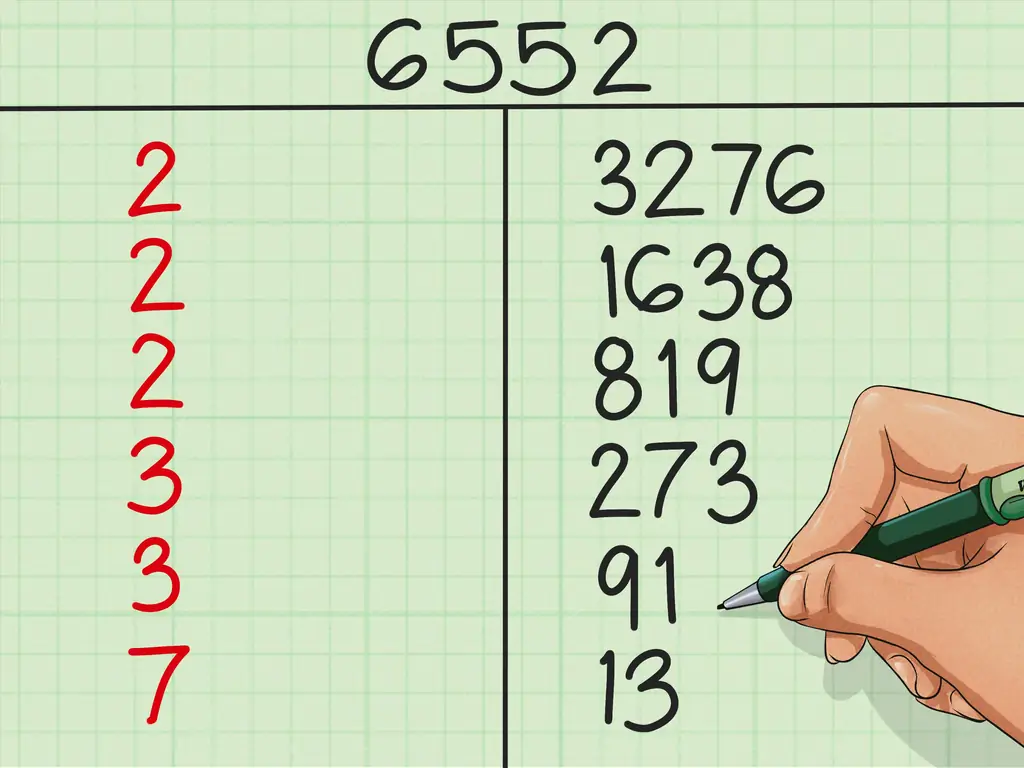
В целях нашего примера давайте выберем 4-значное число для факторизации - 6, 552.

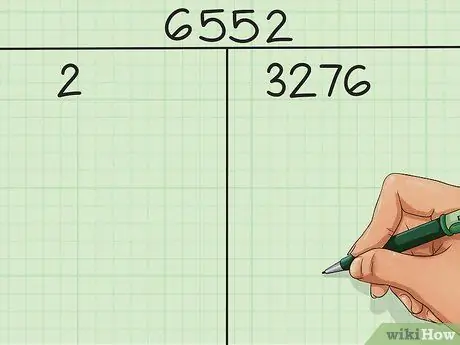
Шаг 2. Разделите ваше число на наименьший из возможных простых множителей

Разделите ваше число на наименьший простой множитель (кроме 1), который делит его равномерно без остатка. Напишите основной множитель в левом столбце и напишите свой ответ напротив него в правом столбце. Как отмечалось выше, четные числа особенно легко начать разложение на множители, потому что их наименьший простой множитель всегда будет равен 2. С другой стороны, нечетные числа будут иметь наименьшие различающиеся простые множители.

• В нашем примере, поскольку 6, 552 четное число, мы знаем, что 2 - его наименьший простой делитель. 6, 552 ÷ 2 = 3, 276. В левом столбце запишем

  Шаг 2., а в правом столбце напишите 3, 276.

Шаг 3. Продолжайте учитывать этот фактор

Затем разложите на множитель число в правом столбце на его наименьший простой множитель, а не на число в верхней части таблицы. Запишите простой множитель в левом столбце и новое число в правом столбце. Продолжайте повторять этот процесс - с каждым повторением число в правом столбце должно уменьшаться.

• Продолжим наш процесс. 3, 276 ÷ 2 = 1, 638, поэтому в нижней части левого столбца мы напишем еще один

  Шаг 2., а внизу правого столбца мы напишем 1, 638. 1, 638 ÷ 2 = 819, поэтому запишем

  Шаг 2. а также 819 внизу двух столбцов, как и раньше.

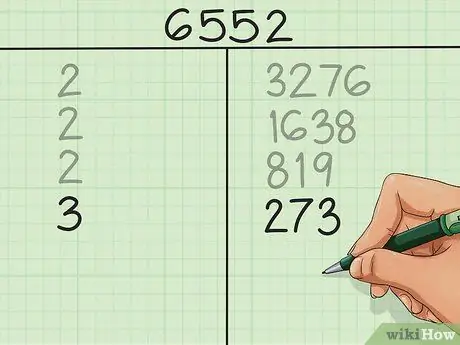
Шаг 4. Разберитесь с нечетными числами, попробовав малые простые множители

Нечетные числа труднее найти наименьший простой множитель четных чисел, потому что они автоматически не имеют 2 в качестве наименьшего простого множителя. Когда вы получите нечетное число, попробуйте разделить его на небольшие простые числа, отличные от 2 - 3, 5, 7, 11 и т. Д. - пока не найдете такое, которое делится без остатка. Это наименьший простой фактор числа.

• В нашем примере мы достигли 819. 819 - нечетное число, поэтому 2 не является множителем 819. Вместо того, чтобы записывать еще 2, мы попробуем следующее простое число: 3. 819 ÷ 3 = 273 без остатка, так что мы запишем

  Шаг 3. а также 273.

• При угадывании множителей следует пробовать все простые числа до квадратного корня из наибольшего найденного множителя. Если ни один из факторов, которые вы пытались до этого момента, не делятся равномерно, вы, вероятно, пытаетесь разложить на множители простое число и, таким образом, закончили процесс разложения.

Шаг 5. Продолжайте, пока не дойдете до 1

Продолжайте делить числа в правом столбце на их наименьший простой множитель, пока не получите простое число в правом столбце. Разделите это число на себя - это поместит число в левый столбец и цифру «1» в правый столбец.

• Завершим факторинг нашего числа. См. Подробную разбивку ниже:

  • Разделим еще раз на 3: 273 ÷ 3 = 91, без остатка, так что запишем

    Шаг 3. а также 91.

  • Давайте попробуем еще раз 3: 91 не имеет 3 в качестве множителя и не имеет следующего младшего простого числа (5) в качестве множителя, но 91 ÷ 7 = 13 без остатка, поэтому мы запишем

    Шаг 7. ан

    Шаг 13..

  • Давайте попробуем еще раз 7: 13 не имеет 7 как множитель или 11 (следующее простое число), но оно есть как множитель: 13 ÷ 13 = 1. Итак, чтобы закончить нашу таблицу, мы запишем

    Шаг 13. ан

    Шаг 1.. Наконец-то мы можем прекратить факторинг.

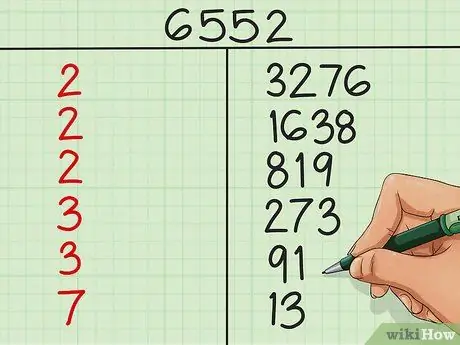
Шаг 6. Используйте числа в левом столбце в качестве множителей исходного числа

Как только вы достигнете 1 в правом столбце, все готово. Цифры, указанные в левой части таблицы, являются вашими факторами. Другими словами, произведение, когда вы умножите все эти числа вместе, будет числом в верхней части таблицы. Если один и тот же множитель встречается несколько раз, вы можете использовать представление экспоненты для экономии места. Например, если в вашем списке факторов четыре двойки, вы можете написать 2⁴ а не 2 × 2 × 2 × 2.

В нашем примере 6 552 = 2³ × 3² × 7 × 13. Это полное разложение 6,552 в простые числа. Независимо от того, в каком порядке умножаются эти числа, произведение будет 6 552.

Видео - с помощью этой службы некоторая информация может быть передана YouTube

подсказки

• Самые низкие простые числа - 2, 3, 5, 7, 11, 13, 17, 19 и 23.
• Некоторые числа можно разложить на множители быстрее, но этот метод работает каждый раз, и в качестве дополнительного бонуса основные множители перечислены в порядке возрастания, когда вы закончите.
• Помните, что мы говорим только о так называемых «натуральных числах», иногда называемых «счетными числами»: 1, 2, 3, 4, 5… Мы не собираемся переходить к отрицательным числам или дробям, которые может оправдать свои собственные статьи
• Если сумма чисел в числителе кратна трем, то тройка является множителем этого числа. (819 = 8 + 1 + 9, что = 18, 1 + 8 = 9. Три - это коэффициент девять, так что это коэффициент 819.)
• Также важна концепция основной число: число, состоящее только из двух факторов: 1 и самого себя. 3 - простое число, потому что его единственные множители - 1 и 3. 4, напротив, имеет множитель 2. Число, которое не является простым, называется составным. (Однако само число 1 не считается ни простым, ни составным - это особый случай.)
• Поймите, что одно число - это фактор другого, большего числа, если оно «делит его чисто», то есть большее число может быть разделено на меньшее число, не оставляя остатка. Например, 6 - это множитель 24, потому что 24 ÷ 6 = 4 без остатка. С другой стороны, 6 - это не коэффициент 25.