Как разделить многочлены: 10 шагов (с изображениями)

Многочлены можно разделить так же, как числовые константы, либо факторизацией, либо делением в столбик. Используемый метод зависит от сложности полиномиального делимого и делителя.

Шаги

Часть 1 из 3: определение того, какой подход использовать

Шаг 1. Посмотрите, насколько сложен делитель

Насколько сложен делитель (многочлен, на который вы делите) по сравнению с делимым (многочлен, на который вы делите), определяет, какой подход лучше.

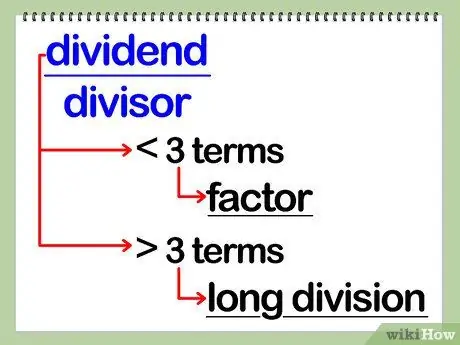
Если делитель является мономом (одночленным многочленом), либо переменной с коэффициентом, либо константой (числом без переменной, следующей за ним), вы, вероятно, можете разложить на множители делимое и отменить один из результирующих множителей и делитель. См. «Факторинг дивидендов» для получения инструкций и примеров.
Если делитель является биномом (двухчленным многочленом), вы можете разложить на множители дивиденд и вычесть один из полученных множителей и делитель.
Если делитель является трехчленным (трехчленным многочленом), вы можете разложить на множители и делимое, и делитель, отменить общий множитель, а затем либо дополнительно вычесть дивиденд, либо использовать деление в столбик.
Если делитель представляет собой многочлен с более чем тремя множителями, вам, вероятно, придется использовать деление в столбик. См. Инструкции и примеры в разделе «Использование длинного полиномиального деления».

Шаг 2. Посмотрите, насколько сложны дивиденды

Если рассмотрение полинома делителя уравнения не говорит вам, следует ли пытаться разложить дивиденд на множители, посмотрите на сам дивиденд.

Если дивиденд состоит из трех или менее членов, вы, вероятно, можете разложить его на множители и отменить делитель.
Если в дивиденде более трех членов, вам, вероятно, придется разделить на него делитель с помощью длинного деления.

Часть 2 из 3: Факторинг дивидендов

Шаг 1. Посмотрите, все ли члены в дивиденде содержат общий множитель с делителем

Если это так, вы можете вычленить это и, вероятно, отменить делитель.

Если вы разделите бином 3x - 9 на 3, вы можете вынести 3 из обоих членов бинома, в результате чего получится 3 (x - 3). Затем вы можете сократить делитель 3, оставив частное x - 3.
Если вы делите двучлен на 24x³ - 18x² на 6x, вы можете вынести 6x из обоих членов бинома, в результате чего получится 6x (4x² - 3). Вы можете сократить делитель 6x, оставив частное 4x² - 3.

Шаг 2. Найдите в дивидендах особые закономерности, говорящие о том, что их можно разложить на множители

Некоторые полиномы отображают члены, которые говорят вам, что их можно разложить на множители. Если один из этих факторов совпадает с делителем, вы можете отменить его, оставив оставшийся фактор как частное. Вот несколько закономерностей, на которые стоит обратить внимание:

Разница полных квадратов. Это бином формы ‘’ a ²Икс² - б ²’’, Где значения ‘’ a ²’’ И ‘’ b ²’’ - идеальные квадраты. Этот бином делится на два бинома (ax + b) (ax - b), где a и b - квадратные корни из коэффициента и константы предыдущего бинома.
Полный квадрат трехчлена. Этот трехчлен имеет вид²Икс² + 2abx + b ². Он множится в (ax + b) (ax + b), что также может быть записано (ax + b)². Если знак перед вторым членом - это знак минус, биномиальные множители будут в форме (ax - b) (ax - b).
Сумма или разница кубиков. Это бином вида a³Икс³ + b³ или³Икс³ - б³, где значения ‘’ a ³’’ И ‘’ b ³’’ - идеальные кубики. Этот бином делится на бином и трехчлен. Сумма кубов множится до (ax + b) (a²Икс² - abx + b²). Разница кубов множится до (ax - b) (a²Икс² + abx + b²).

Шаг 3. Используйте метод проб и ошибок, чтобы разложить дивиденды

Если вы не видите четкой закономерности в дивиденде, которая подсказывала бы вам, как его разложить на множители, вы можете попробовать несколько возможных комбинаций факторинга. Вы можете сделать это, посмотрев сначала на константу и найдя для нее несколько факторов, а затем на коэффициент среднего члена.

Например, если дивиденд равен x² - 3x - 10, вы бы посмотрели на множители 10 и использовали 3, чтобы определить, какая пара множителей верна.
Число 10 можно разбить на множители 1 и 10 или 2 и 5. Поскольку знак перед 10 отрицательным, один из множителей бинома должен иметь отрицательное число перед своей константой.
Число 3 - это разница между 2 и 5, так что это должны быть константы факторных биномов. Поскольку знак перед 3 отрицательный, бином с 5 должен быть тем, у которого отрицательное число. Таким образом, биномиальные множители равны (x - 5) (x + 2). Если делитель является одним из этих двух факторов, этот фактор может быть сокращен, а оставшийся фактор является частным.

Часть 3 из 3: Использование длинного полиномиального деления

Шаг 1. Настройте разделение

Вы записываете длинное деление многочленов так же, как и деление чисел. Дивиденд идет под полосой длинного деления, а делитель - влево.

Если вы делите x² + 11 х + 10 по х +1, х² + 11 x + 10 идет под полосой, а x + 1 идет влево.

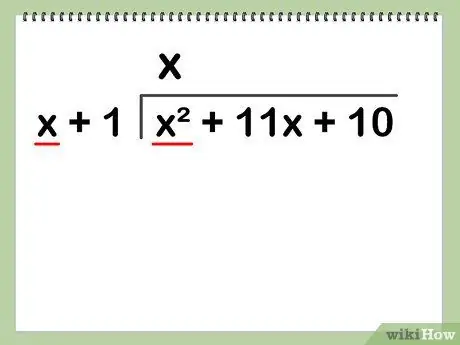
Шаг 2. Разделите первый член делителя на первый член дивиденда

Результат этого деления отображается в верхней части шкалы деления.

В нашем примере, разделив x², первый член делимого на x, первый член делителя дает x. Вы должны написать x в верхней части полосы деления над x².

Шаг 3. Умножьте x в позиции частного на делитель

Напишите результат умножения под крайним левым членом делимого.

Продолжая наш пример, умножение x + 1 на x дает x² + х. Вы должны написать это под первыми двумя условиями дивиденда.

Шаг 4. Вычтите из дивиденда

Для этого сначала поменяйте местами знаки произведения умножения. После вычитания уменьшите оставшиеся члены дивиденда.

Поменять знаки x² + x дает - x² - Икс. Если вычесть это из первых двух членов дивиденда, получится 10x. После уменьшения оставшегося срока дивиденда у вас будет 10x + 10 в качестве промежуточного частного для продолжения процесса деления.

Шаг 5. Повторите предыдущие три шага для промежуточного частного

Вы снова разделите первый член делителя на член промежуточного частного, напишете этот результат над полосой деления после первого члена частного, умножите результат на делитель, а затем вычислите, что вычесть из промежуточное частное.

Поскольку x переходит в 10x 10 раз, вы должны написать «+ 10» после x в позиции частного на шкале деления.
Умножение x +1 на 10 дает 10x + 10. Вы пишете это под промежуточным частным и меняете знаки вычитания, получая -10x - 10.
Когда вы выполняете вычитание, вы получаете остаток 0. Таким образом, разделив x² + 11 x + 10 на x +1 дает частное x + 10. (Вы могли бы получить тот же результат путем факторинга, но этот пример был выбран для упрощения деления.)

подсказки

Если при выполнении деления полинома в столбик у вас есть ненулевой остаток, вы можете сделать эту оставшуюся часть частного, записав его в виде дроби, используя остаток в качестве числителя и делителя в качестве знаменателя. Если бы в нашем примере с длинным делением дивиденд был бы x² + 11 x + 12 вместо x² + 11 x + 10, при делении на x +1 остаток останется 2. Таким образом, полное частное будет записано как: x + 10 + 2x + 1 { displaystyle x + 10 + { frac {2} {x +1}}}
be aware that some algebra books format long polynomial division with the quotient and dividend right-justified, or with the terms presented such that the terms of the same degree within both polynomials are aligned with each other. you will probably find it easier, however, when doing the division by hand, to left-justify the quotient and dividend as described in the steps above.
if your dividend has a gap in the degrees of its terms, such as 3x³+9x²+18, you can insert the missing term with a coefficient of 0, in this case, 0x to make it easier to position the other terms during the division. doing this doesn’t change the dividend’s value.

warnings

when writing the quotient of a polynomial division that includes a fractional term, always use a plus sign between the whole number (or whole variable) term and the fractional term.
keep your columns aligned when doing long polynomial division to avoid subtracting the wrong terms from each other.