Скорость определяется как скорость объекта в заданном направлении. Во многих распространенных ситуациях, чтобы найти скорость, мы используем уравнение v = s / t, где v равно скорости, s равно общему смещению от начальной позиции объекта, а t равно затраченному времени. Однако технически это дает только среднюю скорость объекта на его пути. Используя математический анализ, можно вычислить скорость объекта в любой момент на его пути. Это называется мгновенной скоростью и определяется уравнением v = (ds) / (dt), или, другими словами, производная уравнения средней скорости объекта.
Шаги
Часть 1 из 3: Расчет мгновенной скорости

Шаг 1. Начните с уравнения скорости через смещение
Чтобы получить мгновенную скорость объекта, сначала нам нужно иметь уравнение, которое сообщает нам его положение (с точки зрения смещения) в определенный момент времени. Это означает, что уравнение должно иметь переменную s с одной стороны сам по себе и т на другом (но не обязательно отдельно), например:
s = -1,5 т2+ 10т + 4
-
В этом уравнении переменными являются:
-
-
Смещение = s. Расстояние, на которое объект прошел от исходного положения. Например, если объект движется на 10 метров вперед и на 7 метров назад, его полное смещение составляет 10-7 = 3 метра (не 10 + 7 = 17 метров).
- Время = t. Само собой разумеется. Обычно измеряется в секундах.
-
-

Шаг 2. Возьмите производную уравнения
Производная уравнения - это просто другое уравнение, которое сообщает вам его наклон в любой данный момент времени. Чтобы найти производную формулы смещения, дифференцируйте функцию с помощью этого общего правила поиска производных: Если y = a * x, Производная = a * n * xп-1 Это правило применяется к каждому члену на стороне "t" уравнения.
- Другими словами, начните с рассмотрения «t» части вашего уравнения слева направо. Каждый раз, когда вы достигнете «t», вычтите 1 из экспоненты и умножьте весь член на исходную экспоненту. Любые постоянные члены (члены, которые не содержат "t") исчезнут, потому что они будут умножены на 0. Этот процесс на самом деле не так сложен, как кажется - давайте выведем уравнение на шаге выше в качестве примера:
s = -1,5 т2+ 10т + 4
(2) -1,5 т(2-1) + (1) 10 т1 - 1 + (0) 4 т0
-3т1 + 10т0
- 3т + 10

Шаг 3. Замените s на ds / dt
«Чтобы показать, что наше новое уравнение является производной от первого, мы заменяем« s »обозначением« ds / dt ». Технически это обозначение означает« производную s по t ». Более простой способ думать Из этого просто ds / dt - это просто наклон любой заданной точки в первом уравнении. Например, чтобы найти наклон линии, составленной из s = -1,5t2 + 10t + 4 при t = 5, мы просто подставим «5» в t в его производной.
- В нашем текущем примере готовое уравнение теперь должно выглядеть так:
ds / dt = -3t + 10

Шаг 4. Введите значение t в новое уравнение, чтобы найти мгновенную скорость
Теперь, когда у вас есть производное уравнение, найти мгновенную скорость в любой момент времени очень просто. Все, что вам нужно сделать, это выбрать значение t и подставить его в уравнение производной. Например, если мы хотим найти мгновенную скорость при t = 5, мы просто заменим «5» на t в производной ds / dt = -3 + 10. Затем мы просто решим уравнение следующим образом:
ds / dt = -3t + 10
ds / dt = -3 (5) + 10
ds / dt = -15 + 10 = - 5 метров / сек
Обратите внимание, что выше мы использовали метку «метры в секунду». Поскольку мы имеем дело с смещением в метрах и временем в секундах, а скорость в целом - это просто смещение во времени, этот ярлык уместен
Часть 2 из 3: Графическая оценка мгновенной скорости
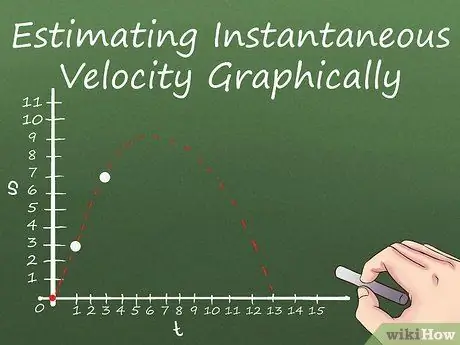
Шаг 1. Постройте график смещения вашего объекта во времени
В предыдущем разделе мы упоминали, что производные - это просто формулы, которые позволяют нам найти наклон в любой точке уравнения, для которого вы берете производную. Фактически, если вы представляете смещение объекта линией на графике, наклон линии в любой заданной точке равен мгновенной скорости объекта в этой точке.
- Чтобы изобразить смещение объекта, используйте ось x для представления времени и ось y для представления смещения. Затем просто нанесите точки, подставляя значения t в уравнение смещения, получая значения s для ваших ответов и отмечая точки t, s (x, y) на графике.
- Обратите внимание, что график может продолжаться ниже оси x. Если линия, представляющая движение вашего объекта, опускается ниже оси x, это означает, что ваш объект движется позади того места, где он начался. Как правило, ваш график не выходит за ось y - мы не часто измеряем скорость объектов, движущихся назад во времени!
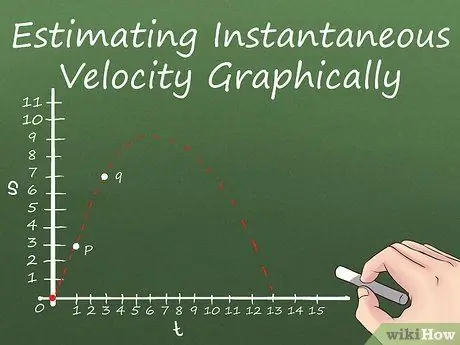
Шаг 2. Выберите одну точку P и точку Q, расположенную рядом с ней на прямой
Чтобы найти наклон линии в одной точке P, мы используем прием, называемый «взятием предела». Принятие предела включает взятие двух точек (P плюс Q, точка рядом с ней) на изогнутой линии и нахождение наклона линии, соединяющей их снова и снова, по мере того, как расстояние между P и Q становится меньше.
Допустим, наша линия смещения содержит точки (1, 3) и (4, 7). В этом случае, если мы хотим найти наклон в (1, 3), мы можем установить (1, 3) = P а также (4, 7) = Q.

Шаг 3. Найдите наклон между P и Q
Наклон между P и Q - это разница значений y для P и Q по сравнению с разницей значений x для P и Q. Другими словами, H = (yQ - уп)/(ИксQ - Иксп), где H - наклон между двумя точками. В нашем примере наклон между P и Q равен:
H = (yQ- уп)/(ИксQ - Иксп)
H = (7 - 3) / (4 - 1)
H = (4) / (3) = 1.33
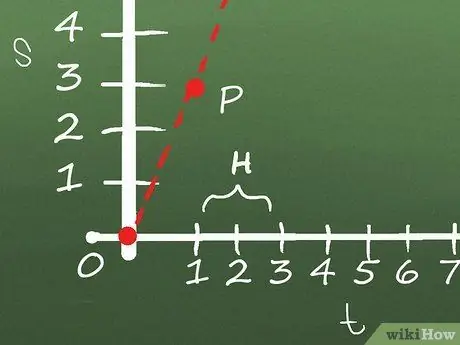
Шаг 4. Повторите несколько раз, перемещая Q ближе к P
Ваша цель здесь - делать расстояние между P и Q все меньше и меньше, пока оно не приблизится к одной точке. Чем меньше расстояние между P и Q, тем ближе наклон ваших крошечных отрезков линии к наклону в точке P. Давайте сделаем это несколько раз для нашего примера уравнения, используя точки (2, 4.8), (1.5, 3.95) и (1.25, 3.49) для Q и наша исходная точка из (1, 3) для P:
Q = (2, 4.8):
H = (4,8 - 3) / (2 - 1)
H = (1,8) / (1) = 1.8
Q = (1,5; 3,95):
H = (3,95 - 3) / (1,5 - 1)
H = (0,95) / (. 5) = 1.9
Q = (1,25, 3,49):
H = (3,49 - 3) / (1,25 - 1)
H = (0,49) / (0,25) = 1.96

Шаг 5. Оцените наклон для бесконечно малого отрезка прямой
По мере того, как Q приближается к P, H будет приближаться к наклону в точке P. В конце концов, на бесконечно малом интервале H будет равняться наклону в P. Поскольку мы не можем измерить или вычислить бесконечно небольшой интервал, мы просто оцениваем наклон в точке P, как только он станет ясным из точек, которые мы пробовали.
-
В нашем примере, когда мы переместили Q ближе к P, мы получили значения 1,8, 1,9 и 1,96 для H. Поскольку эти числа приближаются к 2, мы можем сказать, что
Шаг 2. - хорошая оценка наклона P.
- Помните, что наклон в данной точке линии равен производной уравнения линии в этой точке. Поскольку наша линия показывает смещение нашего объекта во времени и, как мы видели в предыдущем разделе, мгновенная скорость объекта является производной от его смещения в данной точке, мы также можем сказать, что 2 метра в секунду является хорошей оценкой мгновенной скорости при t = 1.
Часть 3 из 3: Примеры задач

Шаг 1. Найдите мгновенную скорость при t = 4 по уравнению перемещения s = 5t.3 - 3т2 + 2т + 9.
Это похоже на наш пример из первого раздела, за исключением того, что мы имеем дело с кубическим уравнением, а не с квадратным уравнением, поэтому мы можем решить его таким же образом.
- Сначала возьмем производную нашего уравнения:
- Затем мы подставим наше значение для t (4):
s = 5 т3- 3т2 + 2т + 9
s = (3) 5t(3 - 1) - (2) 3 т(2 - 1) + (1) 2т(1 - 1) + (0) 9 т0 - 1
15т(2) - 6т(1) + 2т(0)
15т(2) - 6т + 2
s = 15 т(2)- 6т + 2
15(4)(2) - 6(4) + 2
15(16) - 6(4) + 2
240 - 24 + 2 = 218 метров / сек

Шаг 2. Используйте графическую оценку, чтобы найти мгновенную скорость в точке (1, 3) для уравнения перемещения s = 4t.2 - т.
Для этой задачи мы будем использовать (1, 3) в качестве нашей точки P, но нам нужно будет найти несколько других точек рядом с ней, чтобы использовать их в качестве наших точек Q. Затем нужно просто найти наши значения H и произвести оценку.
- Сначала найдем Q точек при t = 2, 1,5, 1,1 и 1,01.
- Далее, давайте получим наши значения H:
- Поскольку наши значения H, кажется, очень близки к 7, мы можем сказать, что 7 метров в секунду является хорошей оценкой мгновенной скорости в точке (1, 3).
s = 4t2- т
t = 2:
s = 4 (2)2 - (2)
4 (4) - 2 = 16 - 2 = 14, поэтому Q = (2, 14)
t = 1,5:
s = 4 (1,5)2 - (1.5)
4 (2,25) - 1,5 = 9 - 1,5 = 7,5, поэтому Q = (1,5, 7,5)
t = 1,1:
s = 4 (1,1)2 - (1.1)
4 (1,21) - 1,1 = 4,84 - 1,1 = 3,74, поэтому Q = (1,1, 3,74)
t = 1,01:
s = 4 (1,01)2 - (1.01)
4 (1.0201) - 1.01 = 4.0804 - 1.01 = 3.0704, поэтому Q = (1,01; 3,0704)
Q = (2, 14):
H = (14 - 3) / (2 - 1)
H = (11) / (1) =
Шаг 11.
Q = (1,5, 7,5):
H = (7,5 - 3) / (1,5 - 1)
H = (4,5) / (. 5) =
Шаг 9.
Q = (1,1, 3,74):
H = (3,74 - 3) / (1,1 - 1)
H = (0,74) / (. 1) = 7.3
Q = (1.01, 3.0704):
H = (3,0704 - 3) / (1,01 - 1)
H = (0,0704) / (0,01) = 7.04
Видео - с помощью этой службы некоторая информация может быть передана YouTube
подсказки
- Чтобы найти ускорение (изменение скорости с течением времени), используйте метод из первой части, чтобы получить уравнение производной для вашей функции смещения. Затем возьмите другую производную, на этот раз производного уравнения. Это даст вам уравнение для нахождения ускорения в данный момент времени - все, что вам нужно сделать, это ввести свое значение для времени.
- Уравнение, связывающее Y (смещение) с X (время), может быть действительно простым, например, Y = 6x + 3. В этом случае наклон постоянный, и нет необходимости находить производную, чтобы найти наклон, то есть, следуя базовой модели Y = mx + b для линейных графиков, 6.
- Смещение похоже на расстояние, но имеет заданное направление, поэтому смещение является вектором, а скорость - скаляром. Смещение может быть отрицательным, а расстояние только положительным.
