Как найти уравнения асимптот гиперболы

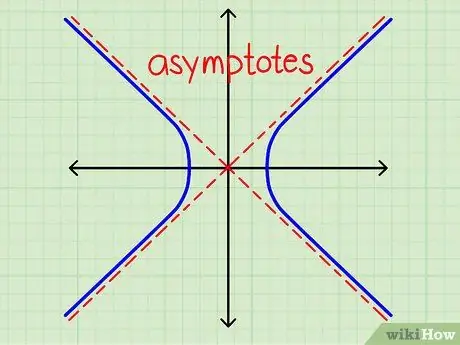
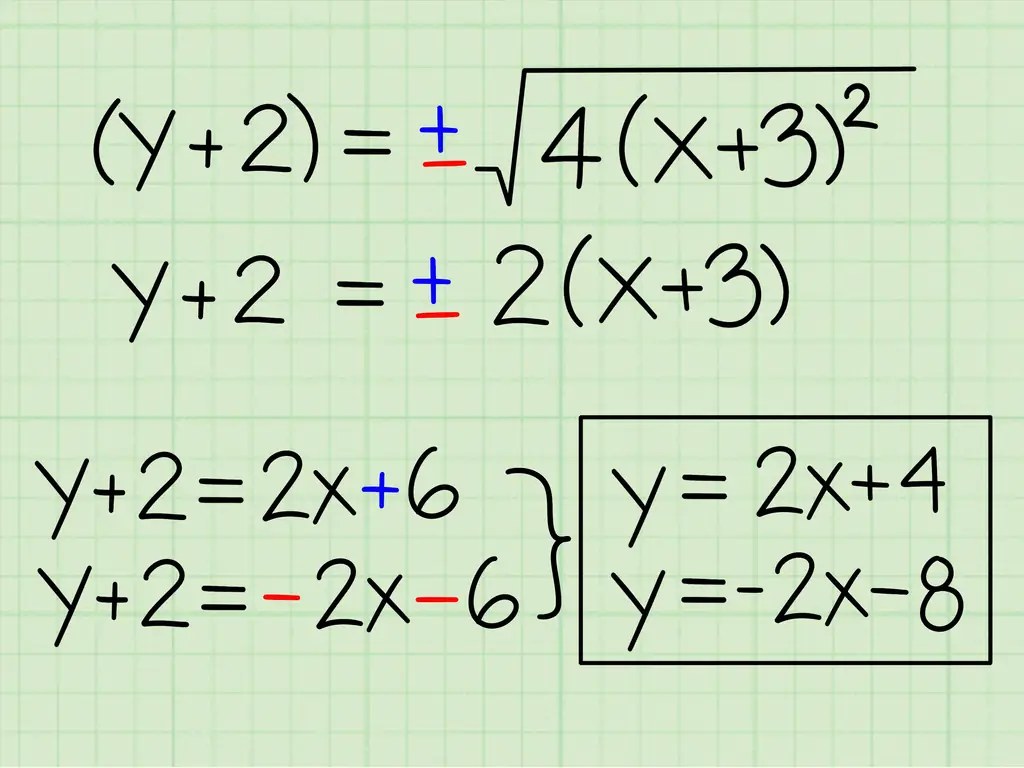Асимптоты гиперболы - это линии, проходящие через центр гиперболы. Гипербола все ближе и ближе подходит к асимптотам, но никогда не достигает их. Есть два разных подхода, которые вы можете использовать для поиска асимптот. Изучение того, как делать и то и другое, может помочь вам понять концепцию.

Шаги

Метод 1 из 2: факторинг

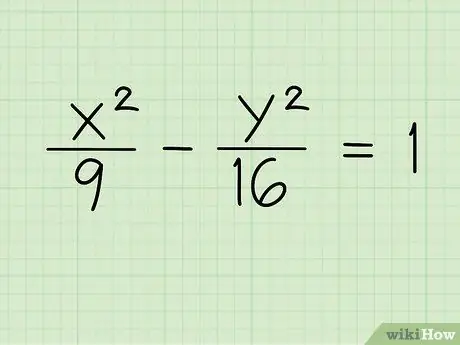
Шаг 1. Запишите уравнение гиперболы в стандартной форме

Начнем с простого примера: гипербола с центром ее начала. Для этих гипербол стандартная форма уравнения имеет вид ^{Икс2/_а2 - у2/_б2 = 1 для гипербол, продолжающихся вправо и влево, или у2/_б2 - Икс2/_а2 = 1 для гипербол, идущих вверх и вниз. Помните, что x и y - переменные, а a и b - константы (обычные числа).}

• Пример 1:

  ^{Икс2/₉ - у2/₁₆ = 1}

• Некоторые учебники и учителя меняют положение a и b в этих уравнениях. Внимательно следите за уравнением, чтобы понять, что происходит. Если вы просто запомните уравнения, вы не будете готовы, когда увидите другие обозначения.

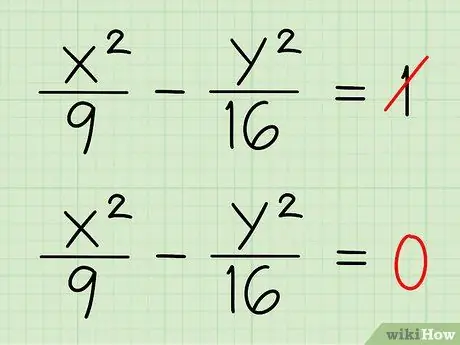
Шаг 2. Установите уравнение равным нулю вместо единицы

Это новое уравнение представляет обе асимптоты, хотя для их разделения потребуется немного больше работы.

• Пример 1:

  ^{Икс2/₉ - у2/₁₆ = 0}

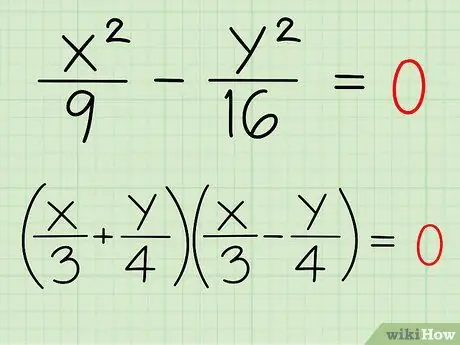
Шаг 3. Разложите новое уравнение на множители

Разложите левую часть уравнения на два произведения. Освежите свою память о разложении квадратичного множителя, если вам нужно, или продолжайте, пока мы продолжим Пример 1:

• В итоге мы получим уравнение в виде (_ ± _) (_ ± _) = 0.
• Первые два члена необходимо перемножить, чтобы получить ^{Икс2/₉, поэтому возьмите квадратный корень и запишите его в этих местах: (Икс/₃ ± _)(Икс/₃ ± _) = 0}
• Аналогичным образом извлеките квадратный корень из ^{у2/₁₆ и поместите его в два оставшихся места: (Икс/₃ ± у/₄)(Икс/₃ ± у/₄) = 0}
• Поскольку других терминов нет, напишите один знак плюс и один знак минус, чтобы остальные члены отменялись при умножении: (^Икс/₃ + ^у/₄)(^Икс/₃ - ^у/₄) = 0

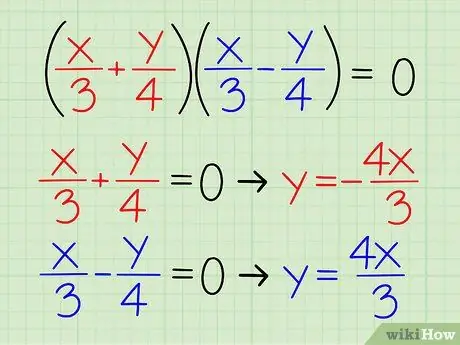
Шаг 4. Разделите множители и решите относительно y

Чтобы получить уравнения для асимптот, разделите два фактора и решите через y.

• Пример 1:

  С (^Икс/₃ + ^у/₄)(^Икс/₃ - ^у/₄) = 0, мы знаем ^Икс/₃ + ^у/₄ = 0 и ^Икс/₃ - ^у/₄ = 0

• Переписать ^Икс/₃ + ^у/₄ = 0 → ^у/₄ = - ^Икс/₃ → у = - ^4x/₃
• Переписать ^Икс/₃ - ^у/₄ = 0 → - ^у/₄ = - ^Икс/₃ → y = ^4x/₃

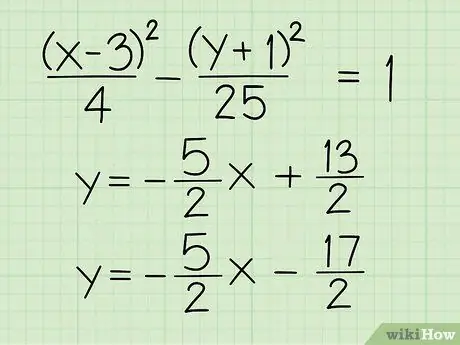
Шаг 5. Попробуйте тот же процесс с более сложным уравнением

Мы только что нашли асимптоты гиперболы с центром в начале координат. Гипербола с центром (h, k) имеет уравнение в виде ^{(х - ч)2/_а2 - (у - к)2/_б2 = 1, или в виде (у - к)2/_б2 - (х - ч)2/_а2 = 1. Вы можете решить их с помощью того же метода факторинга, который описан выше. Просто оставьте члены (x - h) и (y - k) неизменными до последнего шага.}

• Пример 2: ^{(х - 3)2/₄ - (y + 1)2/₂₅ = 1}
• Установите его равным 0 и коэффициент, чтобы получить:
• (^{(х - 3)}/₂ + ^{(y + 1)}/₅)(^{(х - 3)}/₂ - ^{(y + 1)}/₅) = 0
• Разделите каждый множитель и решите, чтобы найти уравнения асимптот:
• ^{(х - 3)}/₂ + ^{(y + 1)}/₅ = 0 → у = -⁵/₂х + ¹³/₂
• (^{(х - 3)}/₂ - ^{(y + 1)}/₅) = 0 → y = ⁵/₂Икс - ¹⁷/₂

Метод 2 из 2: решение Y

Шаг 1. Запишите уравнение гиперболы с y² термин слева.

Этот метод полезен, если у вас есть уравнение в общей квадратичной форме. Даже если это стандартная форма для гипербол, этот подход может дать вам некоторое представление о природе асимптот. Переставьте уравнение так, чтобы y² или (y - k)² срок находится на одной стороне, чтобы начать.

• Пример 3:

  ^{(y + 2)2/₁₆ - (х + 3)2/₄ = 1}

• Добавьте член x к обеим сторонам, затем умножьте каждую сторону на 16:
• (y + 2)² = 16(1 + ^{(х + 3)2/₄)}
• Упрощать:
• (y + 2)² = 16 + 4 (х + 3)²

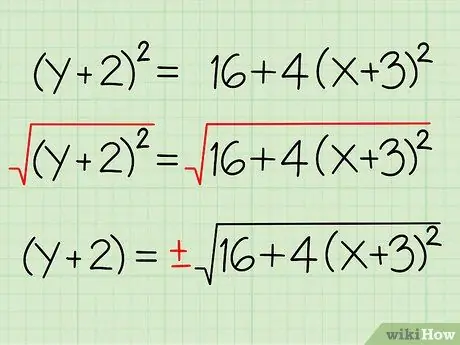
Шаг 2. Извлеките квадратный корень из каждой стороны

Извлеките квадратный корень, но пока не пытайтесь упростить правую часть. Помните, что когда вы извлекаете квадратный корень, есть два возможных решения: положительное и отрицательное. (Например, -2 * -2 = 4, поэтому √4 может быть равно -2, а также 2.) Используйте знак «+» или «-» ±, чтобы отслеживать оба решения.

• √ ((у + 2)²) = √ (16 + 4 (х + 3)²)
• (у + 2) = ± √ (16 + 4 (х + 3)²)

Шаг 3. Просмотрите определение асимптоты

Важно, чтобы вы поняли это, прежде чем переходить к следующему шагу. Асимптота гиперболы - это линия, к которой гипербола становится все ближе и ближе с увеличением x. X никогда не может фактически достичь асимптоты, но если мы будем следовать гиперболе для все больших и больших значений x, мы будем приближаться к асимптоте.

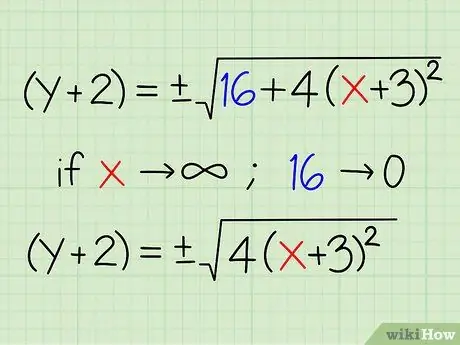
Шаг 4. Скорректируйте уравнение для больших значений x

Поскольку сейчас мы пытаемся найти уравнение асимптоты, нас интересует только x для очень больших значений («приближение к бесконечности»). Это позволяет нам игнорировать определенные константы в уравнении, потому что они вносят очень малую часть по сравнению с членом x. Как только x достигает 99 миллиардов (например), добавление трех настолько мало, что мы можем его игнорировать.

• В уравнении (y + 2) = ± √ (16 + 4 (x + 3)²), когда x приближается к бесконечности, 16 теряет значение.
• (y + 2) = приблизительно ± √ (4 (x + 3)²) для больших значений x

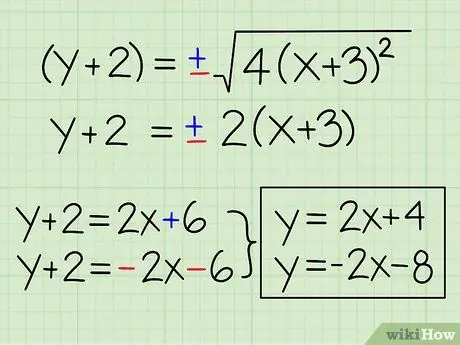
Шаг 5. Решите относительно y, чтобы найти два асимптотических уравнения

Теперь, когда мы избавились от константы, мы можем упростить извлечение квадратного корня. Решите через y, чтобы получить ответ. Не забудьте разделить символ ± на два отдельных уравнения, одно с + и одно с -.

• у + 2 = ± √ (4 (х + 3) ^ 2)
• у + 2 = ± 2 (х + 3)
• y + 2 = 2x + 6 и y + 2 = -2x - 6
• у = 2х + 4 а также у = -2x - 8

Видео - с помощью этой службы некоторая информация может быть передана YouTube

подсказки

• Всегда помните, что уравнение гиперболы и его пара асимптот всегда зависят от константы.
• Прямоугольная гипербола - это гипербола, в которой in a = b = constant = c.
• При работе с прямоугольными гиперболами сначала преобразуйте их в стандартную форму, а затем найдите асимптоты.