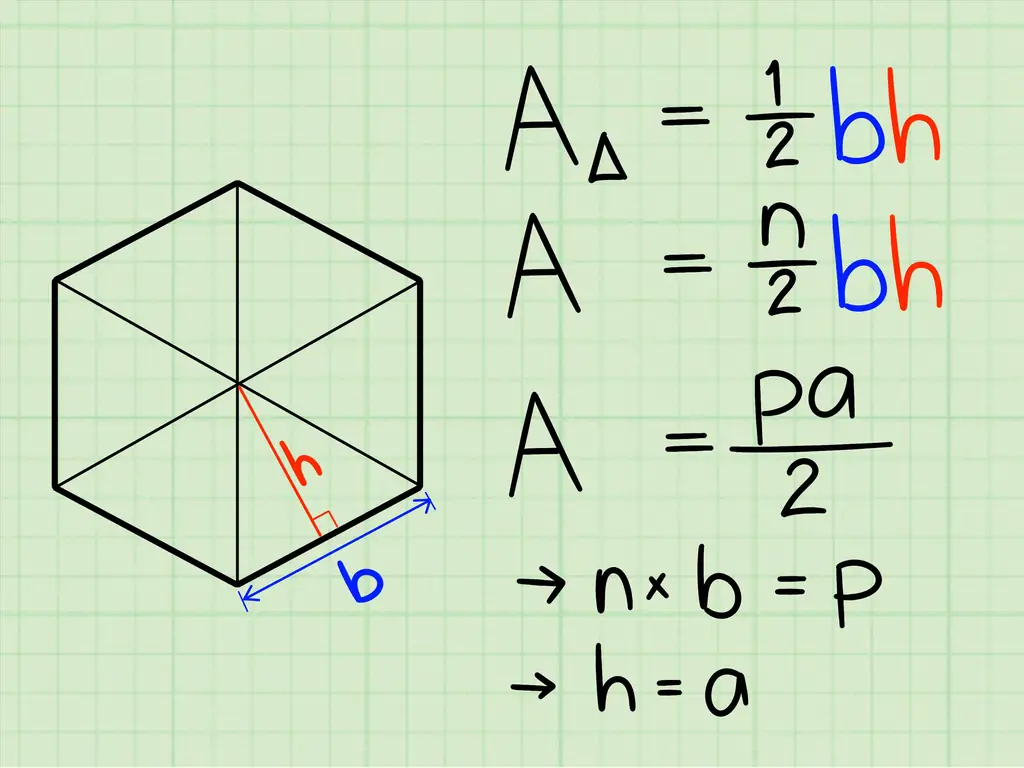Правильный многоугольник - это двумерная выпуклая фигура с равными сторонами и равными по мере углами. Многие многоугольники, такие как четырехугольники или треугольники, имеют простые формулы для определения их площадей, но если вы работаете с многоугольником, у которого больше четырех сторон, то лучше всего использовать формулу, которая использует апофему и периметр формы. Приложив немного усилий, вы можете найти площадь правильных многоугольников всего за несколько минут.
Шаги
Часть 1 из 2: Расчет площади
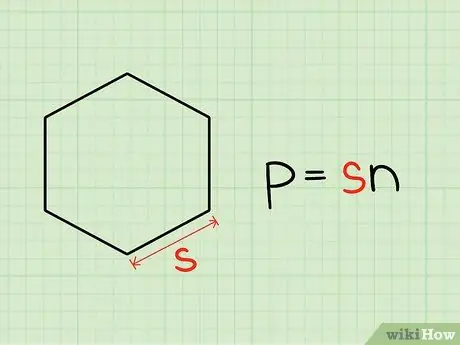
Шаг 1. Рассчитайте периметр
Периметр - это общая длина контура любой двумерной фигуры. Для правильного многоугольника его можно вычислить, умножив длину одной стороны на количество сторон (n).
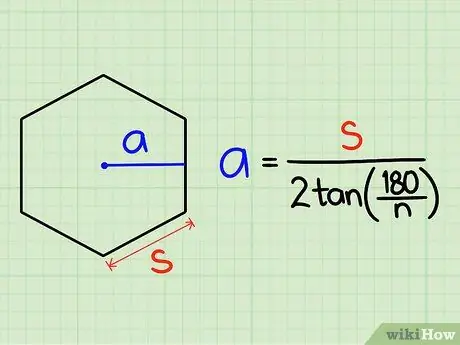
Шаг 2. Определите апофему
Апофема правильного многоугольника - это кратчайшее расстояние от центральной точки до одной из сторон, образующее прямой угол. Это немного сложнее рассчитать, чем периметр.
Формула для расчета длины апофемы такова: длина стороны (сторон), деленная на 2, умноженные на тангенс (тангенс) 180 градусов, деленный на количество сторон (n)
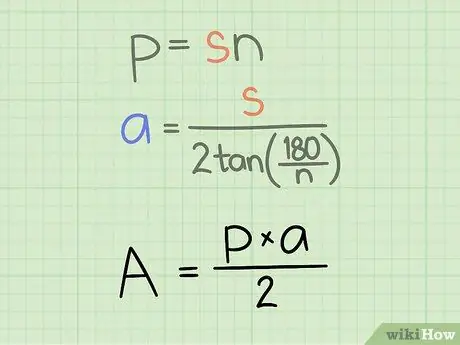
Шаг 3. Знайте правильную формулу
Площадь любого правильного многоугольника определяется по формуле: Площадь = (a x p) / 2, куда а длина апофемы и п периметр многоугольника.
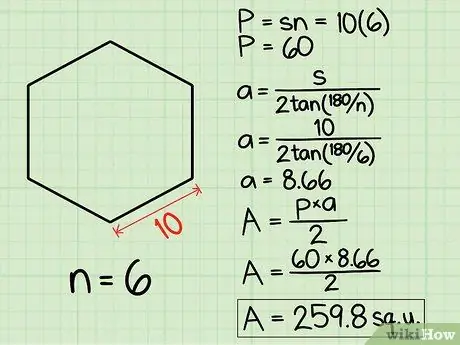
Шаг 4. Подставьте значения а также p в формуле и получите площадь.
В качестве примера возьмем шестиугольник (6 сторон) с длиной стороны 10.
- Периметр равен 6 x 10 (n x s), что равно 60 (поэтому p = 60).
- Апофема рассчитывается по собственной формуле, подставляя 6 и 10 для n и s. Результат 2tan (180/6) равен 1,1547, а затем 10, разделенное на 1,1547, равно 8,66.
- Площадь многоугольника равна Area = a x p / 2, или 8,66, умноженному на 60, деленному на 2. Решение - площадь 259,8 единиц.
- Также обратите внимание, что в уравнении «Площадь» нет скобок, поэтому 8,66, деленное на 2, умноженное на 60, даст вам тот же результат, точно так же, как 60, разделенное на 2, умноженное на 8,66, даст вам тот же результат.
Часть 2 из 2: новое понимание концепций
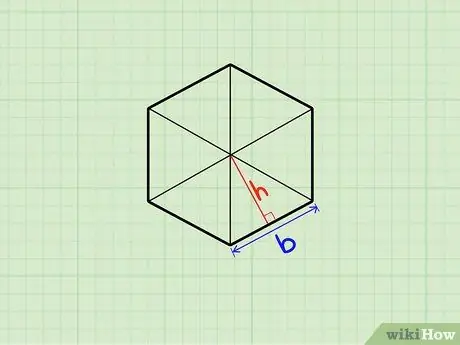
Шаг 1. Поймите, что правильный многоугольник можно рассматривать как набор треугольников
Каждая сторона представляет собой основание треугольника, и в многоугольнике столько треугольников, сколько сторон. Каждый из треугольников имеет одинаковую длину основания, высоту и площадь.
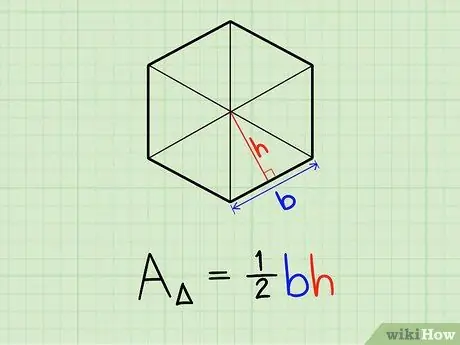
Шаг 2. Запомните формулу площади треугольника
Площадь любого треугольника равна 1/2 длины основания (которая в многоугольнике равна длине стороны), умноженной на высоту (которая совпадает с апофемой в правильном многоугольнике).
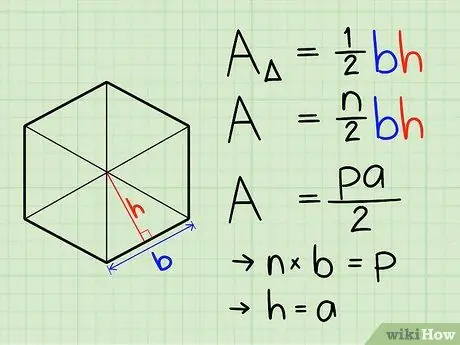
Шаг 3. Посмотрите на сходство
Опять же, формула для правильного многоугольника - это 1/2 апофемы, умноженной на периметр. Периметр - это просто длина одной стороны, умноженная на количество сторон (n); для правильного многоугольника n также представляет количество треугольников, составляющих фигуру. Таким образом, формула - это не что иное, как площадь треугольника, умноженная на количество треугольников в многоугольнике.
Видео - с помощью этой службы некоторая информация может быть передана YouTube
подсказки
Если рисунок вашего многоугольника разделен на треугольники и обозначена площадь одного треугольника, то вам не нужно знать апофему. Просто возьмите площадь этого треугольника и умножьте на количество сторон исходного многоугольника
Помощь по области
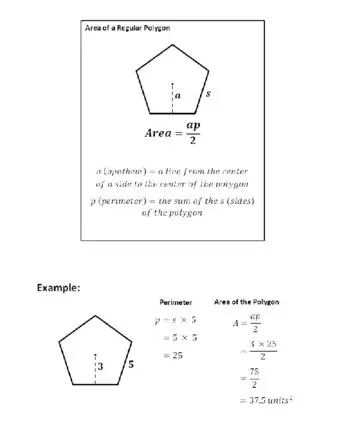
Шпаргалка по площади правильного многоугольника
Поддержка wikiHow и разблокировать все образцы.

Калькулятор площади правильного многоугольника
Поддержка wikiHow и разблокировать все образцы.