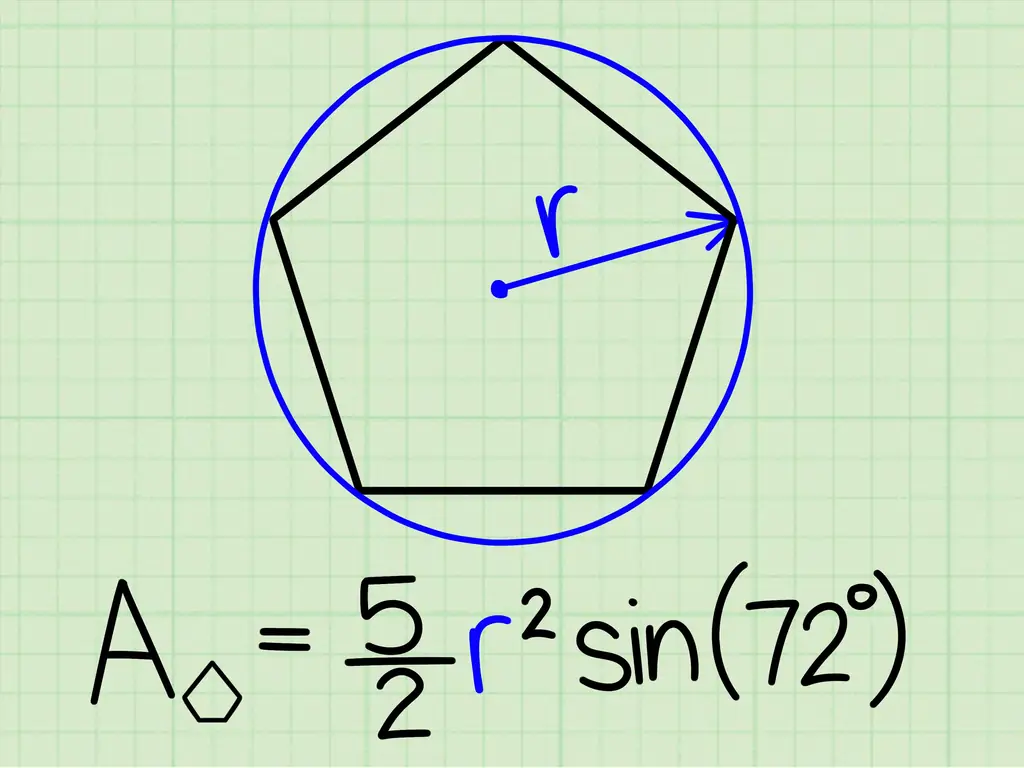Пятиугольник - это многоугольник с пятью прямыми сторонами. Почти все задачи, которые вы найдете на уроке математики, относятся к правильным пятиугольникам с пятью равными сторонами. Есть два распространенных способа найти местность, в зависимости от того, сколько информации у вас есть.
Шаги
Метод 1 из 3: определение площади по длине стороны и апофеме
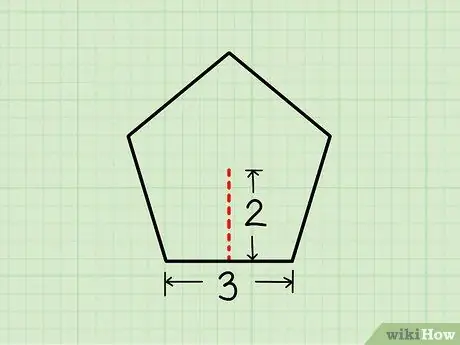
Шаг 1. Начните с длины стороны и апофемы
Этот метод работает для правильных пятиугольников с пятью равными сторонами. Помимо длины стороны, вам понадобится «апофема» пятиугольника. Апофема - это линия от центра пятиугольника к стороне, пересекающая сторону под прямым углом 90º.
- Не путайте апофему с радиусом, который касается угла (вершины), а не середины. Если вы знаете только длину и радиус стороны, перейдите к следующему методу.
-
Мы будем использовать пример пятиугольника с длиной стороны
Шаг 3. единицы и апоте
Шаг 2. единицы.
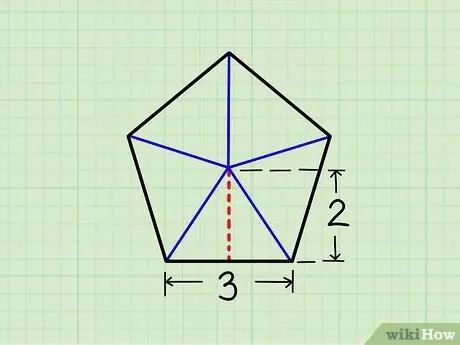
Шаг 2. Разделите пятиугольник на пять треугольников
Нарисуйте пять линий от центра пятиугольника, ведущих к каждой вершине (углу). Теперь у вас есть пять треугольников.
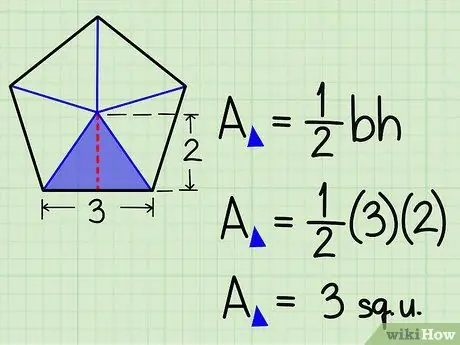
Шаг 3. Вычислите площадь треугольника
У каждого треугольника есть база равняется стороне пятиугольника. Он также имеет рост равняется апофемой пятиугольника. (Помните, что высота треугольника проходит от вершины к противоположной стороне под прямым углом.) Чтобы найти площадь любого треугольника, просто вычислите ½ x основание x высота.
-
В нашем примере площадь треугольника = ½ x 3 x 2 =
Шаг 3. квадратные единицы.

Шаг 4. Умножьте на пять, чтобы найти общую площадь
Мы разделили пятиугольник на пять равных треугольников. Чтобы найти общую площадь, просто умножьте площадь одного треугольника на пять.
-
В нашем примере A (общий пятиугольник) = 5 x A (треугольник) = 5 x 3 =
Шаг 15. квадратные единицы.
Метод 2 из 3: определение площади по длине стороны
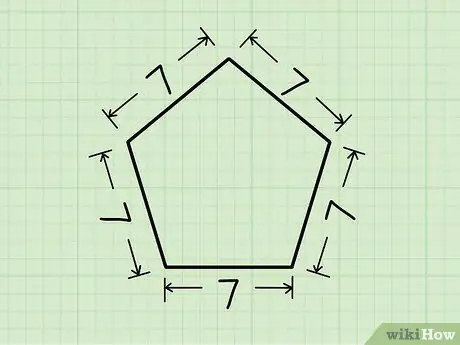
Шаг 1. Начните с длины стороны
Этот метод работает только для правильных пятиугольников, у которых пять сторон равной длины.
-
В этом примере мы будем использовать пятиугольник с длиной стороны
Шаг 7. единицы.
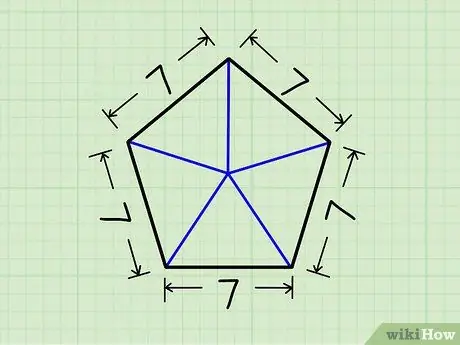
Шаг 2. Разделите пятиугольник на пять треугольников
Проведите линию от центра пятиугольника до любой вершины. Повторите это для каждой вершины. Теперь у вас есть пять треугольников одинакового размера.
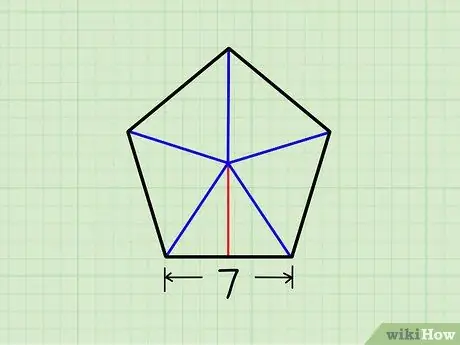
Шаг 3. Разделите треугольник пополам
Проведите линию от центра пятиугольника до основания одного треугольника. Эта линия должна касаться основания под прямым углом 90º, деля треугольник на два равных меньших треугольника.
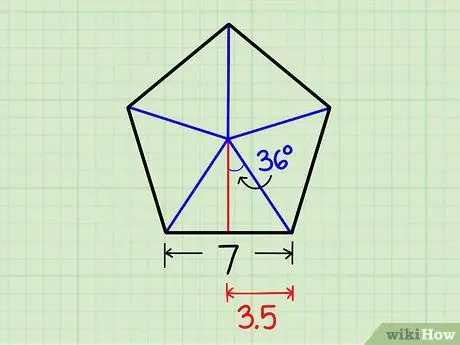
Шаг 4. Обозначьте один из меньших треугольников
Мы уже можем обозначить одну сторону и один угол меньшего треугольника:
- В база треугольника - это ½ стороны пятиугольника. В нашем примере это ½ x 7 = 3,5 единицы.
- В угол в центре пятиугольника всегда 36º. (Начиная с полного центра в 360º, вы можете разделить его на 10 таких меньших треугольников. 360 ÷ 10 = 36, поэтому угол в одном треугольнике равен 36º.)
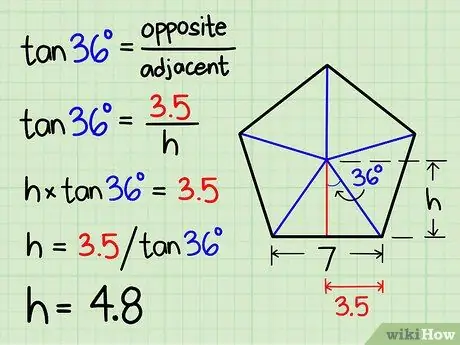
Шаг 5. Рассчитайте высоту треугольника
В рост этого треугольника сторона под прямым углом к краю пятиугольника, ведущая к центру. Мы можем использовать начальную тригонометрию, чтобы найти длину этой стороны:
- В прямоугольном треугольнике касательная угла равна длине противоположной стороны, деленной на длину соседней стороны.
- Сторона, противоположная углу 36º, является основанием треугольника (половина стороны пятиугольника). Сторона, прилегающая к углу 36º, равна высоте треугольника.
- загар (36º) = напротив / рядом
- В нашем примере загар (36º) = 3,5 / рост.
- высота x загар (36º) = 3,5
- высота = 3,5 / загар (36º)
- высота = (около) 4.8 единицы.
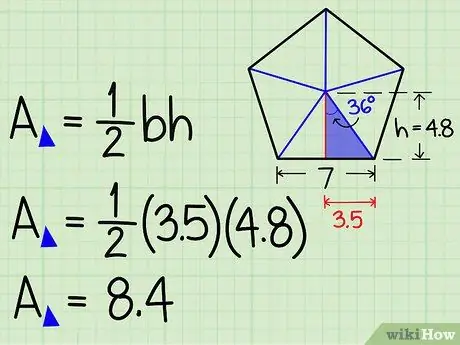
Шаг 6. Найдите площадь треугольника
Площадь треугольника равна ½ основания x высота. (A = ½bh.) Теперь, когда вы знаете высоту, подставьте эти значения, чтобы найти площадь вашего маленького треугольника.
В нашем примере площадь малого треугольника = ½bh = ½ (3,5) (4,8) = 8,4 квадратных единиц

Шаг 7. Умножьте, чтобы найти площадь пятиугольника
Один из этих меньших треугольников покрывает 1/10 площади пятиугольника. Чтобы найти общую площадь, умножьте площадь меньшего треугольника на 10.
В нашем примере площадь всего пятиугольника = 8,4 x 10 = 84 квадратные единицы.
Метод 3 из 3: использование формулы
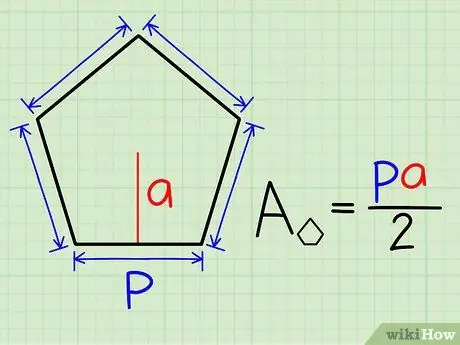
Шаг 1. Используйте периметр и апофему
Апофема - это линия из центра пятиугольника, которая попадает в сторону под прямым углом. Если вам известна его длина, вы можете использовать эту простую формулу
- Площадь правильного пятиугольника = pa / 2, где p = периметр, а = апофема.
- Если вы не знаете периметр, рассчитайте его по длине стороны: p = 5s, где s - длина стороны.
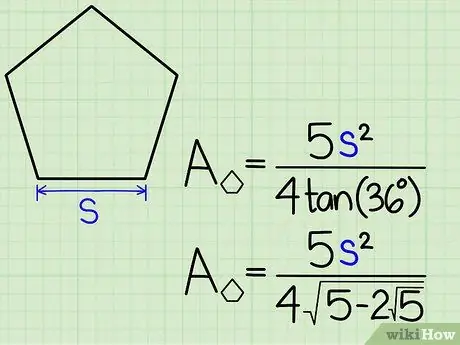
Шаг 2. Используйте длину стороны
Если вам известна только длина стороны, используйте следующую формулу:
- Площадь правильного пятиугольника = (5 с 2) / (4tan (36º)), где s = длина стороны.
- загар (36º) = √ (5-2√5). Поэтому, если в вашем калькуляторе нет функции загара, используйте формулу Area = (5 s 2) / (4√(5-2√5)).
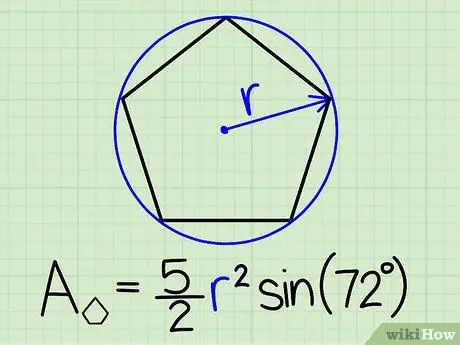
Шаг 3. Выберите формулу, в которой используется только радиус
Вы даже можете найти область, если знаете только радиус. Используйте эту формулу:
Площадь правильного пятиугольника = (5/2) r 2sin (72º), где r - радиус.
Видео - с помощью этой службы некоторая информация может быть передана YouTube
подсказки
- Неправильные пятиугольники или пятиугольники с неравными сторонами труднее изучать. Обычно лучше всего разделить пятиугольник на треугольники и сложить площади каждого треугольника. Вам также может потребоваться нарисовать большую форму вокруг пятиугольника, вычислить его площадь и вычесть площадь лишнего пространства.
- В приведенных здесь примерах используются округленные значения, чтобы упростить математику. Если вы измеряете реальный многоугольник с заданной длиной стороны, вы получите несколько другие результаты для других длин и площади.
- Если возможно, используйте как геометрический метод, так и метод формулы, и сравните результаты, чтобы убедиться, что вы получили правильный ответ. Вы можете получить несколько разные ответы, если введете формулу сразу (так как вы не будете округлять по пути), но они должны быть очень близкими.
- Формулы получены геометрическими методами, аналогичными описанным здесь. Посмотрим, сможешь ли ты придумать, как их придумать. Формулу для радиуса вывести сложнее, чем другие (подсказка: вам понадобится тождество двойного угла).