В каждой физической теории есть константы. Гравитационная постоянная крайне неопределенна.
Когда мы впервые начали формулировать физические законы, мы делали это эмпирически: посредством экспериментов. Сбросьте мяч с башни, как это мог сделать Галилей, и вы сможете измерить, как далеко он упадет, и сколько времени потребуется, чтобы коснуться земли. Отпустите маятник, и вы сможете найти зависимость между длиной маятника и количеством времени, которое требуется для колебания. Если вы сделаете это для ряда расстояний, длин и времени, вы увидите, что возникает зависимость: расстояние до падающего объекта пропорционально квадрату времени; период маятника пропорционален квадратному корню из длины маятника.
Но чтобы превратить эти пропорциональности в знак равенства, вам нужно получить эту константу правильно.
В этих примерах, как и во многих других, эта константа пропорциональности связана с G, гравитационной постоянной. Луна вращается вокруг Земли, планеты вращаются вокруг Солнца, свет искривляется из-за гравитационного линзирования, а кометы теряют энергию, покидая Солнечную систему, и все это пропорционально G. Еще до появления Ньютона, в 1640-х и 1650-х годах, итальянские ученые Франческо Гримальди и Джованни Риччоли сделали первые расчеты гравитационной постоянной, что означает, что это была первая фундаментальная постоянная, когда-либо определенная: еще до того, как Оле Рёмер определил скорость света в 1676.
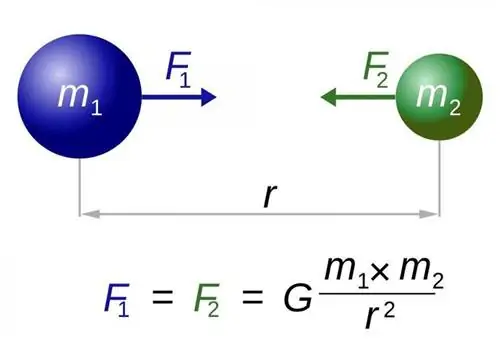
Когда вы берете любые две массы во Вселенной и размещаете их рядом друг с другом, они притягиваются. Согласно законам Ньютона, действительным во всей природе, кроме самых экстремальных условий массы (для больших масс) и расстояния (для малых расстояний), сила притяжения связана с двумя массами, расстоянием между ними и G, гравитационная постоянная. На протяжении веков мы усовершенствовали измерения множества фундаментальных констант с невероятной точностью. Скорость света с точно известна: 299 792 458 м/с. Постоянная Планка ħ, управляющая квантовыми взаимодействиями, имеет значение 1,05457180 × 10^-34 Дж⋅с с погрешностью ±0,000000013 × 10^-34 Дж⋅с.
Но Г? Это совсем другая история.

В 1930-х годах G был измерен и составил 6,67 × 10^-11 Н/кг²⋅м², позже уточненный в 1940-х годах до 6,673 × 10^-11 Н/кг²⋅м², оба ученый Пол Хейл. Как и следовало ожидать, со временем значения становились все лучше и лучше, а неопределенность падала с 0,1 % до 0,04 %, вплоть до 0,012 % в конце 1990-х, в основном благодаря работе Барри Тейлора из NIST.
На самом деле, если вы достанете старую копию буклета Particle Data Group, где они дают фундаментальные константы, вы можете найти там значение G, которое выглядит хорошо: 6,67259 × 10^- 11 Н/кг²⋅м² с погрешностью всего 0,00085 × 10^-11 Н/кг²⋅м².
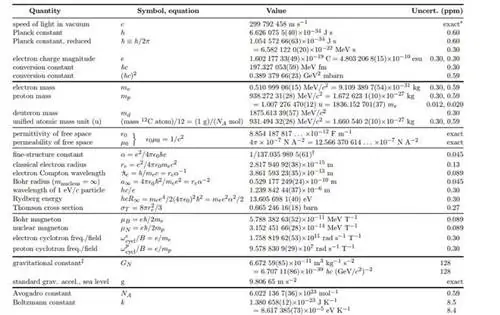
Но потом случилось кое-что смешное.
Позже в том же году проведенные эксперименты показали значение, которое было непоследовательно высоким по сравнению с этими значениями: 6,674 × 10^-11 Н/кг²⋅м². Несколько команд, используя разные методы, получили значения для G, которые противоречили друг другу на уровне 0,15%, что более чем в десять раз превышает неопределенность, о которой сообщалось ранее.
Как это произошло?
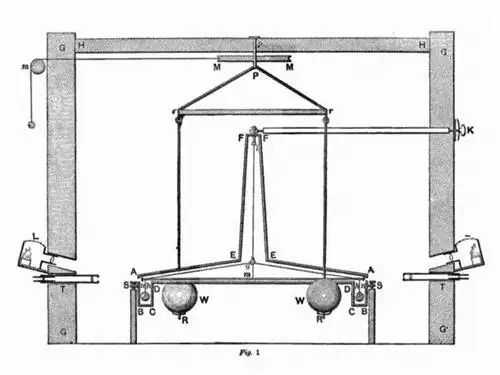
Первое точное измерение гравитационной постоянной, независимое от других неизвестных (таких как масса Солнца или масса Земли), произошло только благодаря экспериментам Генри Кавендиша в конце 18 века. Кавендиш разработал эксперимент, известный как крутильные весы, в котором миниатюрная штанга была подвешена на проволоке и была идеально сбалансирована. Рядом с каждой из масс на обоих концах находились две большие массы, которые гравитационно притягивали малые массы. Величина кручения, которую испытывала миниатюрная штанга, при условии, что массы и расстояния были известны, позволила бы нам экспериментально измерить гравитационную постоянную G.
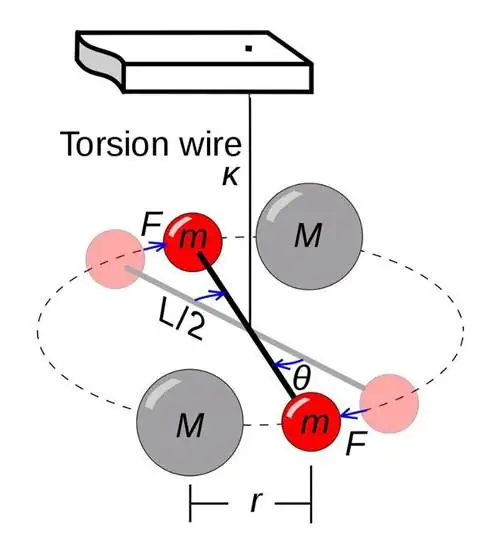
Есть серьезные подозрения, что одним из основных действующих факторов был хорошо известный психологический фактор предвзятости подтверждения. Если все ваши коллеги получают такие измерения, как 6,67259 × 10^-11 Н/кг²⋅м², вы можете разумно ожидать, что получите что-то вроде 6,67224 × 10^-11 Н/кг²⋅м², или 6,67293 × 10^-11 Н/м². кг²⋅м², но если вы получили что-то вроде 6,67532 × 10^-11 Н/кг²⋅м², вы, вероятно, предположили бы, что сделали что-то не так.
Вы бы искали возможные источники ошибок, пока не нашли бы их. И вы будете проводить эксперимент снова и снова, пока не получите что-то разумное: что-то, что хотя бы соответствует 6,67259 × 10^-11 Н/кг²⋅м².
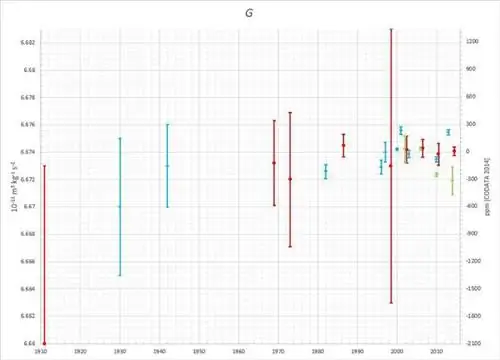
Вот почему это было таким шоком, когда в 1998 году очень осторожная команда получила результат, отличающийся на впечатляющие 0,15% от предыдущих результатов, когда было заявлено, что ошибки в этих более ранних результатах быть более чем в десять раз ниже этой разницы. В ответ NIST отбросил ранее указанные неопределенности, а значения были внезапно усечены, чтобы дать не более четырех значащих цифр, с добавлением гораздо больших неопределенностей.
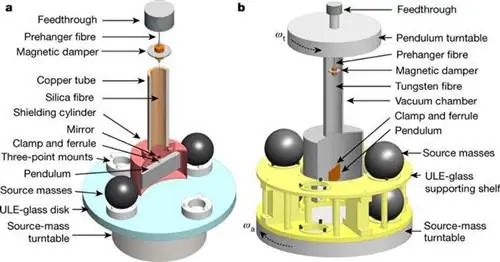
Вращательные весы и крутильные маятники, вдохновленные оригинальным экспериментом Кавендиша, продолжают лидировать в измерении G, опережая более поздние методы экспериментов по атомной интерферометрии. Фактически, только на прошлой неделе команда из Китая заявила, что получила самое точное измерение G из двух независимых измерений: 6,674184 × 10^-11 Н/кг²⋅м² и 6,674484 × 10^-11 Н/кг²⋅м², с неопределенностью всего 11 частей на миллион для каждого.
Эти значения могут согласовываться друг с другом с точностью до двух стандартных отклонений, но они не согласуются с другими измерениями, выполненными другими группами за последние 15 лет, которые варьируются от 6,6757 × 10^ -11 Н/кг²⋅м² и всего 6,6719 × 10^-11 Н/кг²⋅м². В то время как другие фундаментальные константы известны с точностью от 8 до 14 значащих цифр, погрешности в G от тысяч до миллиардов раз больше.
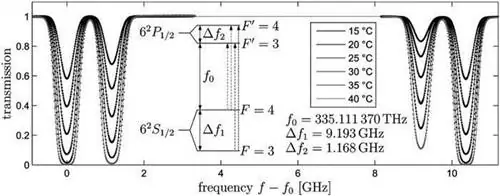
Гравитационная постоянная Вселенной, G, была первой из когда-либо измеренных констант. Тем не менее, более чем через 350 лет после того, как мы впервые определили ее значение, поистине смущает то, насколько плохо известно наше знание этой константы по сравнению со всеми другими константами. Мы используем эту константу во множестве измерений и расчетов, от гравитационных волн до пульсарной синхронизации и расширения Вселенной. Тем не менее, наша способность определять его основана на мелкомасштабных измерениях, сделанных прямо здесь, на Земле. Мельчайшие источники неопределенности, от плотности материалов до сейсмических колебаний по всему земному шару, могут влиять на наши попытки определить ее. До тех пор, пока мы не сможем работать лучше, везде, где важно гравитационное явление, будет существовать неотъемлемая, неприятно большая неопределенность. На дворе 2018 год, а мы до сих пор не знаем, насколько на самом деле сильна гравитация.
