Математика и религия воплощают внушающие благоговение вечные истины.

Ключевые выводы
- На первый взгляд, математика и религия имеют мало общего, но вызывают схожие чувства у своих приверженцев.
- Оба занятия требуют многих лет интенсивных занятий, часто перемежающихся катарсическими моментами «ага».
- Постижение неуловимой вечной истины вызывает чувство благоговения и радости, независимо от того, является ли это понимание математическим или теологическим.
В память о математике Эмми Нётер после ее смерти в 1935 году Альберт Эйнштейн написал в New York Times благодарственное письмо, восхваляя ее открытия, в то же время извлекая более важные жизненные уроки из бескорыстной работы мыслителей. как она, которая освещает человеческий разум. Он говорит, что математика - это «поэзия логических идей». Намекая на успех Нётер, он поясняет: «В этом стремлении к логической красоте открываются духовные формулы, необходимые для более глубокого проникновения в законы природы».
Слово «духовный» - удивительное прилагательное для «формулы», не так ли? Слово «элегантный», возможно, было бы более привычным выбором, и тем не менее Эйнштейн выбрал свои слова, чтобы подчеркнуть более глубокий уровень математической красоты.
Религиозный язык часто используется математиками, даже среди тех, кто не особенно набожен. Пол Эрдёш, известный плодовитый математик, который любил называть Бога Верховным Фашистом, также любил говорить о «Книге», которую хранит Бог, в которой записаны все самые прекрасные доказательства. Однажды он пошутил: «Вам не обязательно верить в Бога, но вы должны верить в Книгу». Эта незримая Книга была явным намеком на вневременность математических идей, существование и постоянство которых соответствует вечной природе, которую некоторые ожидают от божественных истин.
Чем математика похожа на религию
Занятия математикой и религиозные занятия во многом схожи и вызывают схожие чувства и отклики у своих приверженцев. Однако это наблюдение не является универсальным утверждением о религиозных убеждениях математических мыслителей. На протяжении всей математической истории мы находим множество приверженцев различных религиозных традиций - на ум приходят Рамануджан, Агнеси, Эйлер, аль-Хорезми или даже пифагорейцы. Однако многие математики являются атеистами или агностиками. Опрос членов Национальной академии, проведенный в 1998 году, показывает, что математики в этой организации менее религиозны, чем широкая публика (хотя они немного более религиозны, чем другие ученые). Тем не менее, у тех, кто занимается математическим опытом, и у тех, кто занимается религиозным опытом, много общего.
Такая общность отчасти объясняется объяснительной силой как математики, так и религии. Математика предлагает понимание физических явлений. Религия предлагает понимание человеческой природы. Поэтому естественно искать у них мудрости в соответствующих областях. Их истины не всегда очевидны, иногда для этого требуются годы изучения. И их интерпретации или приложения иногда нужно оспаривать.
Оба занятия также вознаграждают борьбу - долгое послушание следованию своим заповедям - наградой в виде проницательных озарений. Годы изучения математики позволяют визуализировать скрытые структуры мира способами, которые становятся второй натурой. Точно так же годы благочестивой преданности дают здоровое нравственное видение, так что человек без колебаний поступает правильно, когда это видение вступает в противоречие с его эгоистичной природой. В этом росте есть радость и награда.
Кроме того, оба занятия предлагают возможность неожиданности: «ага» моменты мгновенной и внушающей страх переориентации, когда решения сложных проблем внезапно становятся ясными. Например, во многих религиях важным вопросом является вопрос о том, как искупить грехи. Неожиданная возможность благодати в искуплении греха - это поразительное решение, мало чем отличающееся от неожиданного решения сложной математической задачи. В каждом случае следуют аллилуйи восторга или облегчения.
Этот ритм медитации, перемежающийся возможностью радостного удивления, означает, что и математический опыт, и религиозный опыт могут предложить убежище и надежду. Во время пандемии COVID продажи головоломок резко возросли. Почему? Потому что во время больших страданий люди ищут развлечения, а разгадывание головоломок - это приятная форма математического мышления, которая не ограничивается только математиками. Решение головоломки приносит радость, а опыт борьбы с головоломками учит нас надеяться, что с каждой новой головоломкой появится ответ. Благочестивый может заменить «загадку» на «молитву» в предыдущем предложении без особых изменений в настроении. Таким образом, размышление над загадкой или молитвой в надежде на их решение - как утешение от мирских стрессов - не так уж и отличается.
Математика и бессмертие
И в математике, и в большинстве религий человек сталкивается лицом к лицу с реальностью бессмертных объектов, которые мы не можем видеть. Религиозных людей часто высмеивают за веру и взаимодействие с нефизическим сверхъестественным Богом. И тем не менее, все такие насмешники научились считать, взаимодействовать и рассуждать с нефизическими платоническими представлениями о целых числах и даже применять их к тому, что мы называем (напротив) «реальным миром». Математика связывает нас «с бессмертием в форме вечных математических законов», как однажды заметил историк математики Д. Э. Смит. Кроме того, многие ученые-ученые удивлялись тому, как вообще может происходить такое взаимодействие. Сам Эйнштейн спрашивал: «Как может быть, что математика, будучи в конце концов продуктом человеческой мысли, независимой от опыта, так замечательно подходит к объектам реальности?» Другими словами, нас должно удивлять, что математические объекты Платона так конструктивно взаимодействуют с реальным миром, но мы принимаем это чудо как должное.
И в математических, и в духовных занятиях постигаются истины такой трансцендентной глубины, что они вызывают трепет и благоговение. Достоинство человека, развращающая природа греха, важность справедливости и сила прощения - все это истины, которые можно глубоко прочувствовать в религиозном опыте. Точно так же знакомство с красотой симметрии или глубокой связью между разрозненными идеями в математике может вызвать глубокое изумление в математическом опыте. Иногда эти встречи - лишь проблески, намеки на существование чего-то большего и невидимого.
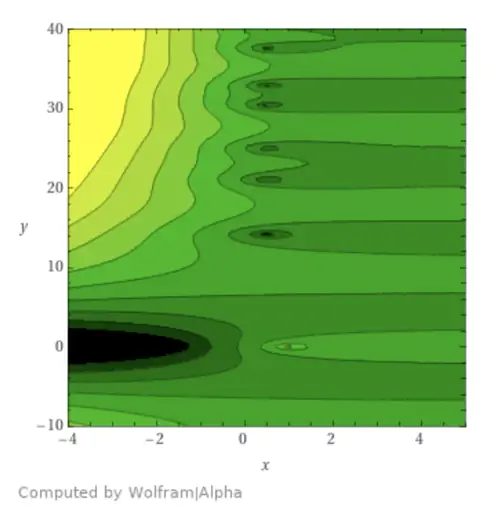
Несколько нулей дзета-функции Римана проявляются в виде темных пятен вдоль вертикальной линии x=½.
Математик, заметивший, что собственные значения случайных матриц обнаруживают поразительное сходство с нулями дзета-функции Римана, задается вопросом: является ли эта красивая связь совпадением, или же это дразнящий ключ к какому-то более глубокая реальность? Точно так же правоверный может увидеть божественную руку в человеческих событиях там, где другие видят только совпадения. И верующие, встречаясь с божественным, чувствуют себя обязанными поклоняться. Эйнштейн выражал похожее чувство: «Если во мне есть что-то, что можно назвать религиозным, то это безграничное восхищение устройством мира, насколько наша наука может его раскрыть». Ученые не чужды поклонению.
Эта общность опыта между математическими занятиями и религиозными занятиями может стать мостом для понимания, связаны ли ваши интересы с многочисленным, сверхъестественным или ни с тем, ни с другим. Даже если у вас нет эмоциональной связи с математической формулой или религиозным катехизисом (и то, и другое может показаться утомительным), вы можете начать понимать, почему это делают другие. Формула имеет объяснительную силу. Он представляет собой проницательное озарение - кульминацию борьбы и надежду понять что-то глубокое. Это иллюстрирует способность людей взаимодействовать с невидимыми, абстрактными истинами, которые влияют на наш мир. И если, подобно Эйнштейну, увидеть трансцендентную важность формул Эмми Нётер для человеческого прогресса и понимания законов природы, тогда действительно: возможно, такие прозрения уместно назвать духовными.
