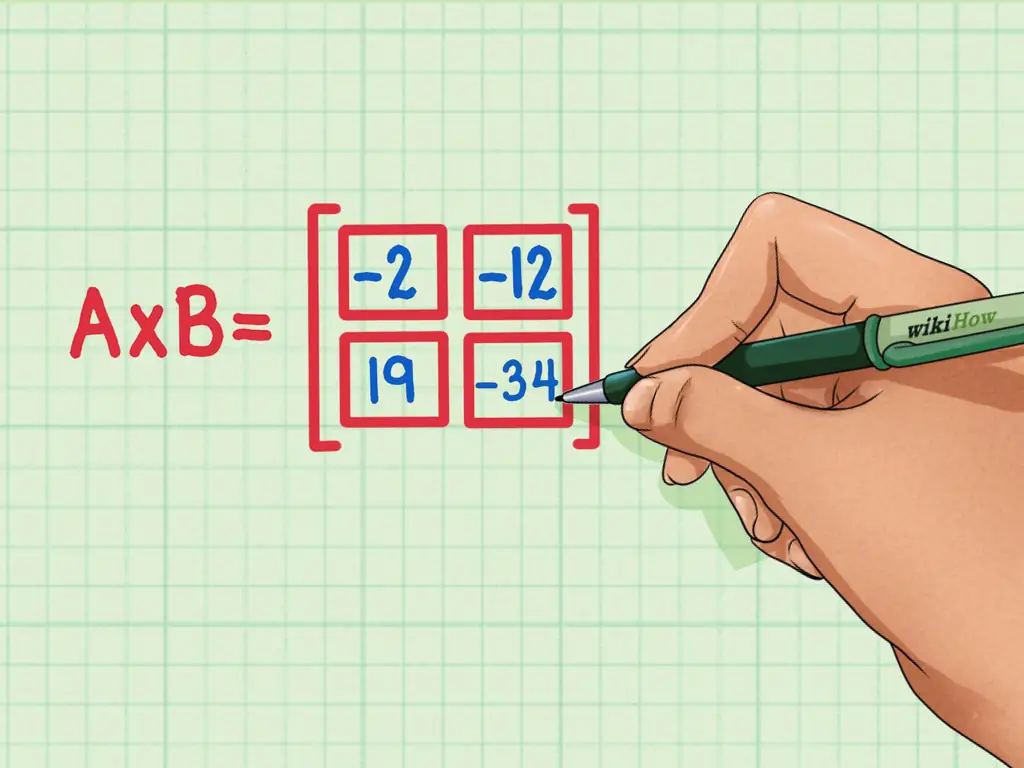Матрица - это прямоугольное расположение чисел, символов или выражений в строках и столбцах. Чтобы умножить матрицы, вам нужно умножить элементы (или числа) в строке первой матрицы на элементы в строках второй матрицы и сложить их произведения. Вы можете умножать матрицы всего за несколько простых шагов, которые требуют сложения, умножения и правильного размещения результатов.
Шаги
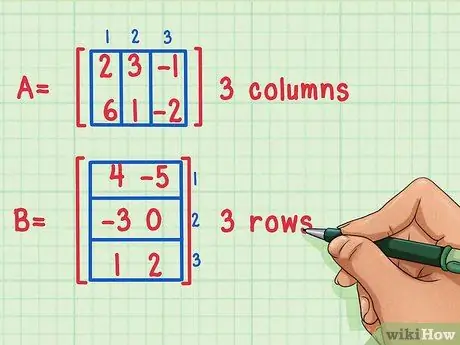
Шаг 1. Подтвердите, что матрицы можно умножать
Вы можете умножать матрицы только в том случае, если количество столбцов первой матрицы равно количеству строк во второй матрице.
Эти матрицы можно умножать, потому что первая матрица, Матрица A, имеет 3 столбца, а вторая матрица, Матрица B, имеет 3 строки
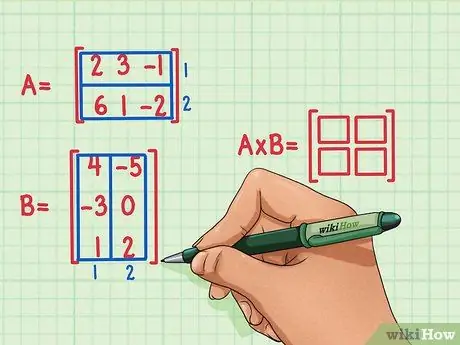
Шаг 2. Отметьте размеры матричного изделия
Создайте новую пустую матрицу, которая будет отмечать размеры матричного продукта, произведения двух матриц. Матрица, представляющая произведение Матрицы A и Матрицы B, будет иметь такое же количество строк, что и первая матрица, и такое же количество столбцов, как вторая матрица. Вы можете нарисовать пустые поля, чтобы указать количество строк и столбцов в этой матрице.
- Матрица A имеет 2 строки, поэтому матричный продукт будет иметь 2 строки.
- Матрица B имеет 2 столбца, поэтому матричный продукт будет иметь 2 столбца.
- Матричный продукт будет иметь 2 строки и 2 столбца.
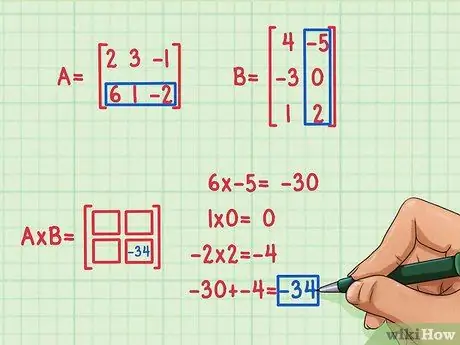
Шаг 3. Найдите первое скалярное произведение
Чтобы найти скалярное произведение, вам нужно умножить первый элемент в первой строке на первый элемент первого столбца, второй элемент первой строки на второй элемент первого столбца и третий элемент в первой строке. третьим элементом в первом столбце. Затем добавьте их продукты, чтобы найти скалярное произведение.
Допустим, вы решили найти элемент в 2nd ряд и 2nd столбец (нижний правый) матричного произведения первым. Вот как это сделать:
- 6 х -5 = -30
- 1 х 0 = 0
- -2 х 2 = -4
- -30 + 0 + (-4) = -34
-
Скалярное произведение равно -34, и оно находится в правом нижнем углу матричного произведения.
При умножении матриц скалярное произведение будет занимать позицию строки первой матрицы и столбца второй матрицы. Например, когда вы нашли скалярное произведение нижней строки матрицы A и правого столбца матрицы B, ответ, -34, попал в нижнюю строку и правый столбец матричного произведения
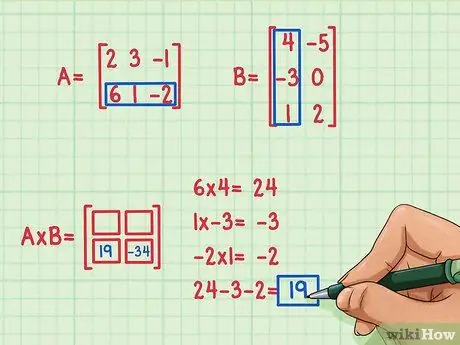
Шаг 4. Найдите второе скалярное произведение
Допустим, вы хотите найти термин в нижнем левом углу матричного произведения. Чтобы найти этот член, вам просто нужно умножить элементы в нижней строке первой матрицы на элементы в первом столбце второй матрицы, а затем сложить их. Используйте тот же метод, который вы использовали для умножения первой строки и столбца - найдите скалярное произведение опять таки.
- 6 х 4 = 24
- 1 х (-3) = -3
- (-2) х 1 = -2
- 24 + (-3) + (-2) = 19
- Скалярное произведение равно -19, и оно находится в нижнем левом углу матричного произведения.
Шаг 5. Найдите два оставшихся скалярных произведения
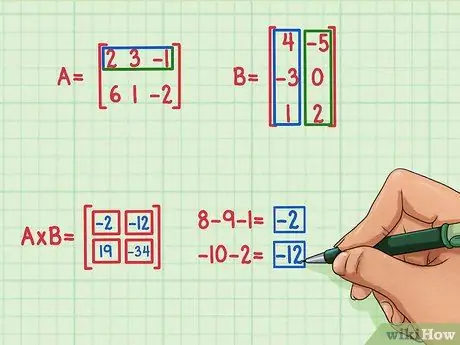
Чтобы найти член в верхнем левом углу матричного произведения, начните с нахождения скалярного произведения верхней строки матрицы A и левого столбца матрицы B. Вот как вы это делаете:
- 2 х 4 = 8
- 3 х (-3) = -9
- (-1) х 1 = -1
- 8 + (-9) + (-1) = -2
-
Скалярное произведение равно -2, и оно находится в верхнем левом углу матричного произведения.
Чтобы найти член в правом верхнем углу матричного произведения, просто найдите скалярное произведение верхней строки матрицы A и правого столбца матрицы B. Вот как вы это делаете:
- 2 х (-5) = -10
- 3 х 0 = 0
- (-1) х 2 = -2
- -10 + 0 + (-2) = -12
- Скалярное произведение равно -12, и оно находится в правом верхнем углу матричного произведения.
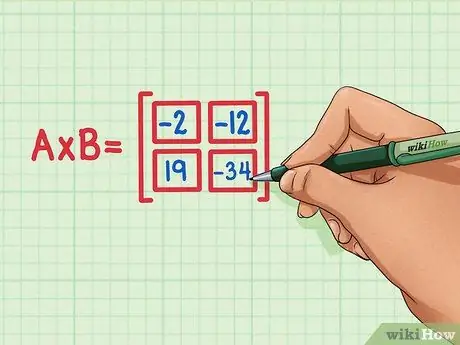
Шаг 6. Убедитесь, что все четыре скалярных произведения находятся в правильном месте в матричном произведении
19 должно быть внизу слева, -34 должно быть внизу справа, -2 должно быть вверху слева, а -12 должно быть вверху справа.
Видео - с помощью этой службы некоторая информация может быть передана YouTube
подсказки
- Выпишите свои суммы. Умножение матриц включает в себя множество вычислений, и очень легко отвлечься и потерять представление о том, какие числа вы умножаете.
- Использование сегментов вместо линий может привести к неправильным ответам. Если линия, представляющая строку, должна быть расширена, чтобы пересечь столбец, увеличьте ее! Это просто метод визуализации, который упрощает определение строки и столбца, которые следует использовать для разработки каждого элемента продукта.
- Произведение двух матриц должно иметь такое же количество строк, что и первая матрица, и такое же количество столбцов, как вторая матрица.