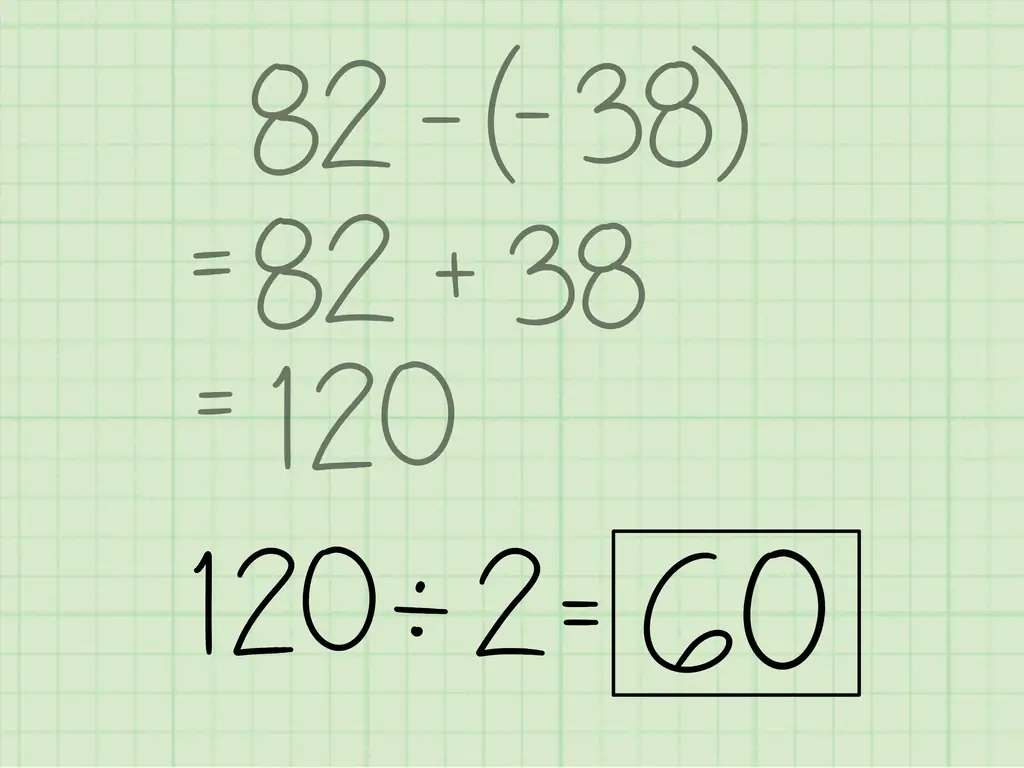Вычислить площадь многоугольника можно так же просто, как найти площадь правильного треугольника, или сложнее, как найти площадь неправильной одиннадцатигранной формы. Если вы хотите узнать, как найти площадь множества многоугольников, просто выполните следующие действия.
Шаги
Помощь по области
Шпаргалка по площади правильного многоугольника

Калькулятор площади правильного многоугольника

Шпаргалка по площади неправильного многоугольника
Часть 1 из 3: Найдите площадь правильных многоугольников по их апофемам
Шаг 1. Запишите формулу для определения площади правильного многоугольника
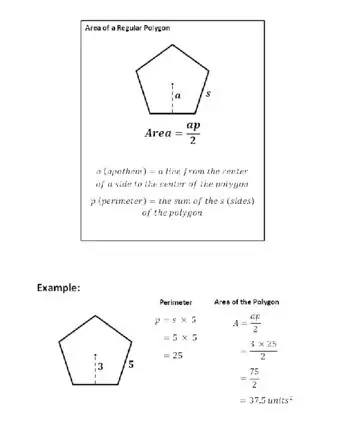
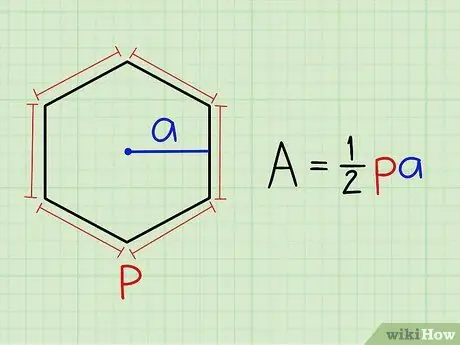
Чтобы найти площадь правильного многоугольника, все, что вам нужно сделать, это следовать этой простой формуле: площадь = 1/2 x периметр x апофема. Вот что это значит:
- Периметр = сумма длин всех сторон
- Апофема = сегмент, который соединяет центр многоугольника с серединой любой стороны, перпендикулярной этой стороне.
Шаг 2. Найдите апофему многоугольника
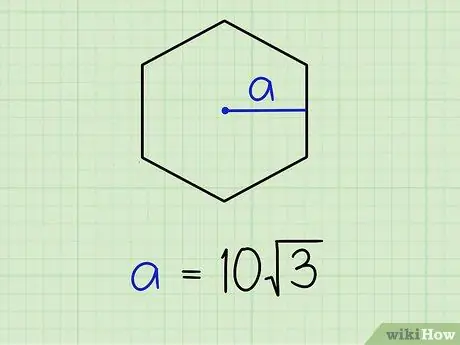
Если вы используете метод апофемы, то апофема будет предоставлена вам. Допустим, вы работаете с шестиугольником с апофемой длиной 10√3.
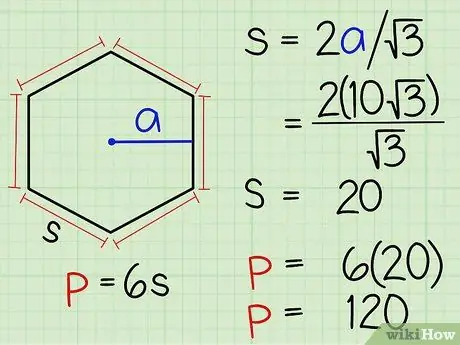
Шаг 3. Найдите периметр многоугольника
Если периметр предусмотрен для вас, значит, вы почти закончили, но, вероятно, вам нужно немного поработать. Если вам предоставлена апофема и вы знаете, что работаете с обычным многоугольником, вы можете использовать ее для определения периметра. Вот как это сделать:
- Думайте об апофеме как о стороне «x√3» треугольника 30-60-90. Вы можете думать об этом так, потому что шестиугольник состоит из шести равносторонних треугольников. Апофема разрезает одну из них пополам, образуя треугольник с углами 30-60-90 градусов.
- Вы знаете, что сторона, лежащая под углом 60 градусов, имеет длину = x√3, сторона, поперечная от угла 30 градусов, имеет длину = x, а сторона, поперечная от угла 90 градусов, имеет длину = 2x. Если 10√3 представляет собой «x√3», то вы можете видеть, что x = 10.
- Вы знаете, что x = половина длины нижней стороны треугольника. Удвойте его, чтобы получить полную длину. Длина нижней стороны треугольника составляет 20 единиц. У шестиугольника шесть сторон, поэтому умножьте 20 x 6, чтобы получить 120, периметр шестиугольника.
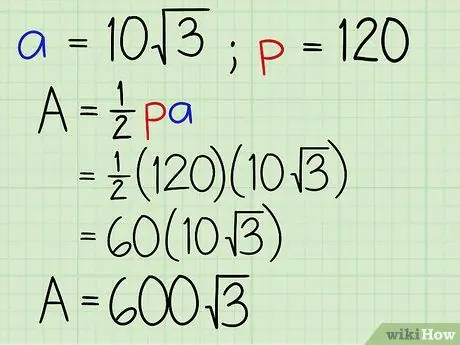
Шаг 4. Подставьте апофему и периметр в формулу
Если вы используете формулу: площадь = 1/2 x периметр x апофема, то вы можете подставить 120 для периметра и 10√3 для апофемы. Вот как это будет выглядеть:
- площадь = 1/2 x 120 x 10√3
- площадь = 60 x 10√3
- площадь = 600√3

Шаг 5. Упростите ответ
Возможно, вам потребуется указать свой ответ в десятичной форме, а не в форме квадратного корня. Просто воспользуйтесь калькулятором, чтобы найти ближайшее значение для √3 и умножьте его на 600. √3 x 600 = 1, 039,2. Это ваш окончательный ответ.
Часть 2 из 3: Определение площади правильных многоугольников по другим формулам
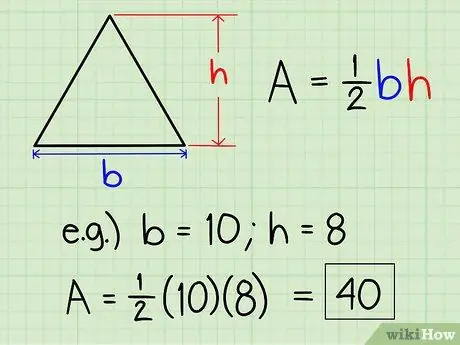
Шаг 1. Найдите площадь правильного треугольника
Если вы хотите найти площадь правильного треугольника, все, что вам нужно сделать, это следовать этой формуле: площадь = 1/2 x основание x высота.
Если у вас есть треугольник с основанием 10 и высотой 8, то площадь = 1/2 x 8 x 10 или 40
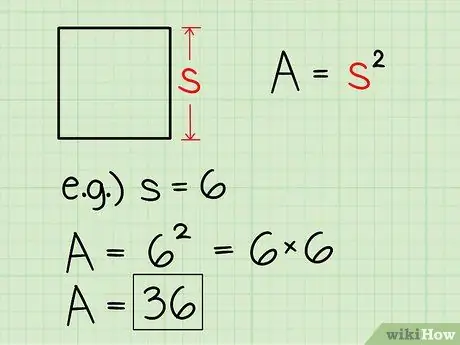
Шаг 2. Найдите площадь квадрата
Чтобы найти площадь квадрата, возведите в квадрат длину одной стороны. На самом деле это то же самое, что умножить основание квадрата на его высоту, потому что основание и высота одинаковы.
Если у квадрата длина стороны 6, то площадь будет 6 x 6, или 36
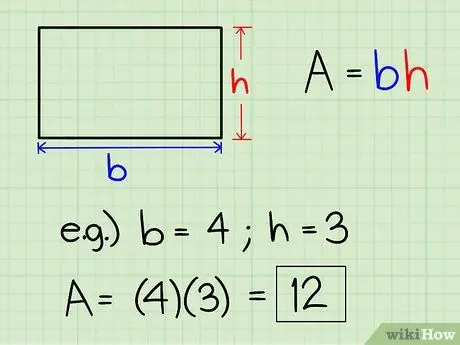
Шаг 3. Найдите площадь прямоугольника
Чтобы найти площадь прямоугольника, просто умножьте основание на высоту.
Если основание прямоугольника 4, а высота 3, тогда площадь прямоугольника будет 4 x 3, или 12
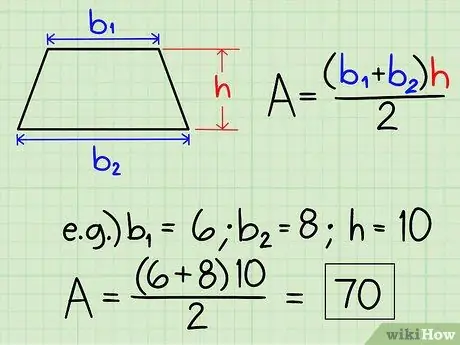
Шаг 4. Найдите площадь трапеции
Чтобы найти площадь трапеции, вам просто нужно следовать этой формуле: площадь = [(основание 1 + основание 2) x высота] / 2.
Допустим, у вас есть трапеция с основаниями длиной 6 и 8 и высотой 10. Площадь простая [(6 + 8) x 10] / 2, которую можно упростить до (14 x 10) / 2., или 140/2, что составляет площадь 70
Часть 3 из 3: Нахождение площади неправильных многоугольников
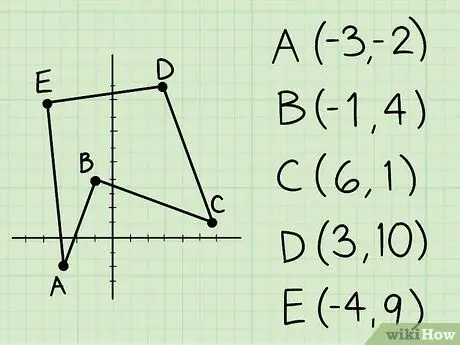
Шаг 1. Запишите координаты вершин неправильного многоугольника
Определение площади неправильного многоугольника можно найти, зная координаты вершин.
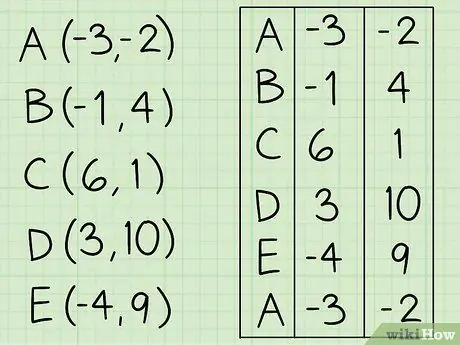
Шаг 2. Создайте массив
Перечислите координаты x и y каждой вершины многоугольника в порядке против часовой стрелки. Повторите координаты первой точки внизу списка.

Шаг 3. Умножьте координату x каждой вершины на координату y следующей вершины
Добавьте результаты. Сумма этих продуктов 82.
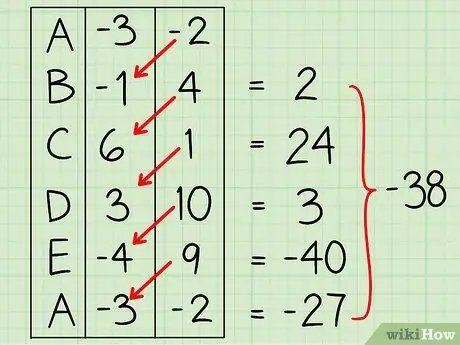
Шаг 4. Умножьте координату y каждой вершины на координату x следующей вершины
Опять же, сложите эти результаты. Сумма этих товаров -38.
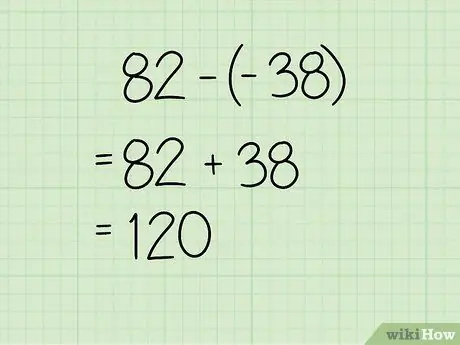
Шаг 5. Вычтите сумму вторых произведений из суммы первых произведений
Вычтем -38 из 82 и получим 82 - (-38) = 120.
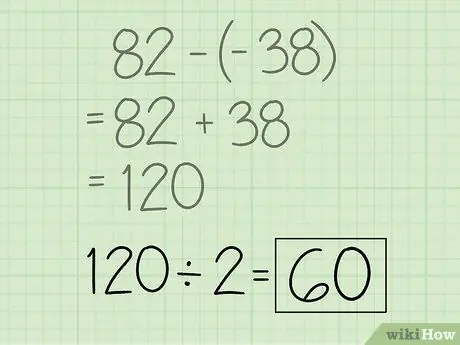
Шаг 6. Разделите эту разницу на 2, чтобы получить площадь многоугольника
Просто разделите 120 на 2, чтобы получить 60, и все готово.
подсказки
- Если вы перечислите точки по часовой стрелке, а не против часовой стрелки, вы получите отрицательную величину площади. Следовательно, это можно использовать как инструмент для идентификации циклического пути или последовательности заданного набора точек, образующих многоугольник.
- Эта формула вычисляет площадь с ориентацией. Если вы используете его на фигуре, где две линии пересекаются, как восьмерка, вы получите область, окруженную против часовой стрелки, минус область, окруженную по часовой стрелке.