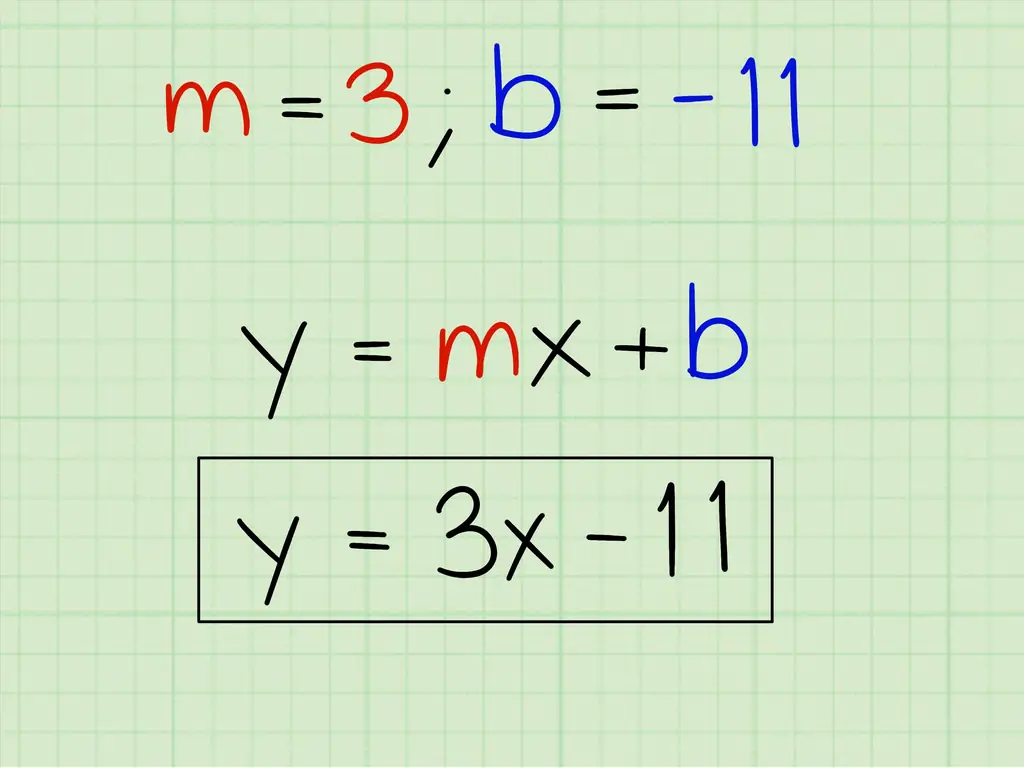Серединный перпендикуляр - это линия, которая разрезает отрезок, соединяющий две точки точно пополам под углом 90 градусов. Чтобы найти серединный перпендикуляр двух точек, все, что вам нужно сделать, это найти их среднюю точку и отрицательную обратную точку и вставить эти ответы в уравнение для линии в форме пересечения наклона. Если вы хотите узнать, как найти серединный перпендикуляр к двум точкам, просто выполните следующие действия.
Шаги
Метод 1 из 2: сбор информации
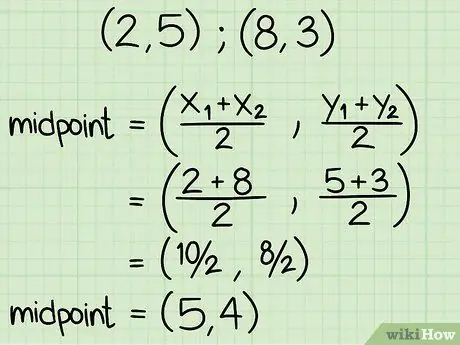
Шаг 1. Найдите середину двух точек
Чтобы найти середину двух точек, просто подставьте их в формулу средней точки: [(x1 + х2) / 2, (y1 + y2) / 2]. Это означает, что вы просто находите среднее значение координат x и y двух наборов точек, которое приводит вас к средней точке двух координат. Допустим, мы работаем с (x1, y1) координаты (2, 5) и (x2, y2) координаты (8, 3). Вот как вы найдете среднюю точку для этих двух точек:
- [(2+8)/2, (5 +3)/2] =
- (10/2, 8/2) =
- (5, 4)
- Координаты середины точек (2, 5) и (8, 3) равны (5, 4).

Шаг 2. Найдите наклон двух точек
Чтобы найти наклон двух точек, просто подставьте точки в формулу наклона: (y2 - у1) / (Икс2 - Икс1). Наклон линии измеряет расстояние ее вертикального изменения по сравнению с расстоянием ее горизонтального изменения. Вот как найти наклон линии, проходящей через точки (2, 5) и (8, 3):
- (3-5)/(8-2) =
- -2/6 =
-
-1/3
Наклон линии -1/3. Чтобы найти этот наклон, вам нужно уменьшить 2/6 до самого низкого значения, 1/3, поскольку и 2, и 6 делятся на 2 без остатка

Шаг 3. Найдите отрицательную величину, обратную наклону двух точек
Чтобы найти отрицательную величину, обратную наклону, просто возьмите обратную величину наклона и измените знак. Вы можете получить отрицательную обратную величину числа, просто перевернув координаты x и y и изменив знак. Обратное значение 1/2 равно -2/1, или просто -2; обратное значение -4 равно 1/4.
Отрицательная величина, обратная -1/3, равна 3, потому что 3/1 является обратной величиной 1/3, а знак был изменен с отрицательного на положительный
Метод 2 из 2: вычисление уравнения прямой
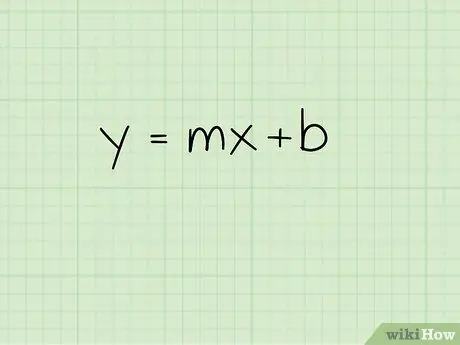
Шаг 1. Напишите уравнение прямой в форме пересечения наклона
Уравнение линии в форме пересечения наклона: y = mx + b, где любые координаты x и y в строке представлены буквами «x» и «y», «m» представляет наклон линии, а «b» представляет точку пересечения линии по оси Y. Y-пересечение - это место, где линия пересекает ось Y. Записав это уравнение, вы можете начать находить уравнение серединного перпендикуляра двух точек.
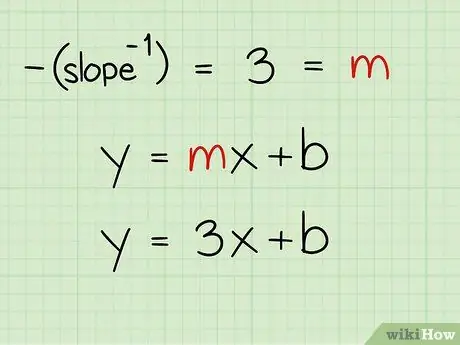
Шаг 2. Подставьте в уравнение обратную величину, обратную исходному уклону
Отрицательная обратная величина наклона точек (2, 5) и (8, 3) равна 3. Буква «m» в уравнении представляет наклон, поэтому подставьте 3 в «m» в уравнении у = mx + b.
- 3 у = mx + b =
- у = 3x + b

Шаг 3. Вставьте точки средней точки в линию
Вы уже знаете, что середина точек (2, 5) и (8, 3) равна (5, 4). Поскольку серединный перпендикуляр проходит через середину двух линий, вы можете подставить координаты средней точки в уравнение прямой. Просто вставьте (5, 4) в координаты x и y линии.
- (5, 4) - y = 3x + b =
- 4 = 3 (5) + Ь =
- 4 = 15 + б
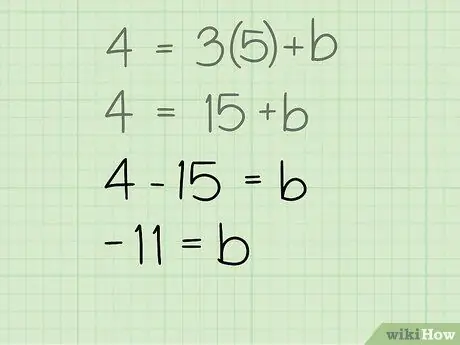
Шаг 4. Найдите перехват
Вы нашли три из четырех переменных в уравнении линии. Теперь у вас достаточно информации, чтобы найти оставшуюся переменную «b», которая является точкой пересечения оси y этой линии. Просто выделите переменную «b», чтобы найти ее значение. Просто вычтите 15 из обеих частей уравнения.
- 4 = 15 + Ь =
- -11 = b
- b = -11
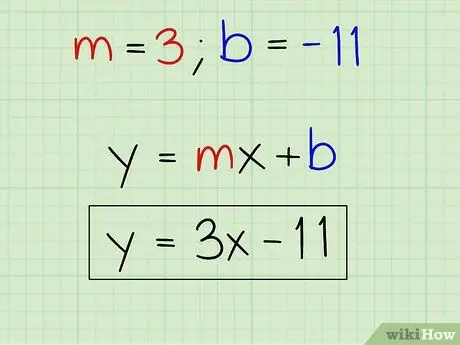
Шаг 5. Напишите уравнение срединного перпендикуляра
Чтобы написать уравнение серединного перпендикуляра, вам просто нужно вставить наклон линии (3) и точку пересечения оси Y (-11) в уравнение линии в форме пересечения угла наклона. Вы не должны вводить какие-либо термины в координаты x и y, потому что это уравнение позволит вам найти любую координату на линии, подключив любую координату x или любую координату y.
- у = mx + b
- у = 3х - 11
- Уравнение для серединного перпендикуляра точек (2, 5) и (8, 3): y = 3x - 11.