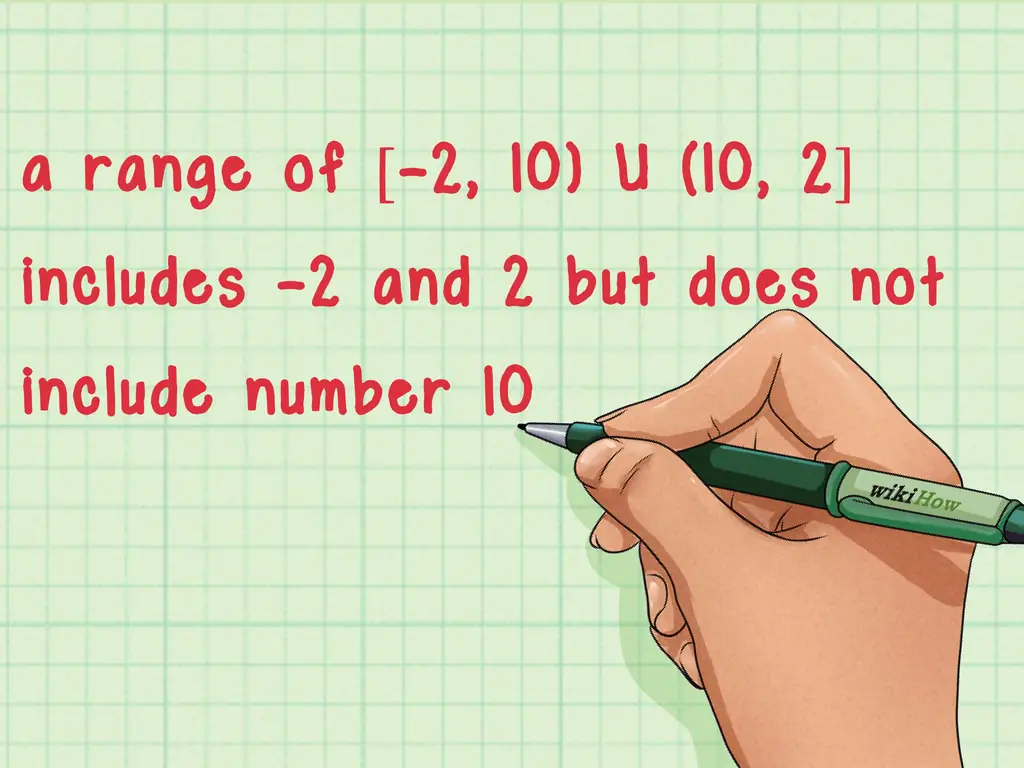Каждая функция содержит два типа переменных: независимые переменные и зависимые переменные, значения которых буквально «зависят» от независимых переменных. Например, в функции y = f (x) = 2 x + y x является независимым, а y зависит (другими словами, y является функцией от x). Допустимые значения для данной независимой переменной x вместе называются «областью». Допустимые значения для данной зависимой переменной y вместе называются «диапазоном».
Шаги
Часть 1 из 3: Поиск области определения функции

Шаг 1. Определите тип функции, с которой вы работаете
Область действия функции - это все значения x (горизонтальная ось), которые дадут вам действительный вывод значения y. Функциональное уравнение может быть квадратным, дробным или содержать корни. Чтобы вычислить область определения функции, вы должны сначала оценить члены в уравнении.
- Квадратичная функция имеет вид ax2 + bx + c: f (x) = 2x2 + 3x + 4
- Примеры функций с дробями: f (x) = (1/Икс), f (x) = (х + 1)/(х - 1), так далее.
- Функции с корнем включают: f (x) = √x, f (x) = √ (x2 + 1), f (x) = √-x и т. Д.

Шаг 2. Напишите домен в правильной нотации
При написании домена функции используются как скобки [,], так и круглые скобки (,). Вы используете скобку, когда номер включен в домен, и скобку, когда домен не включает номер. Буква U обозначает объединение, которое соединяет части домена, которые могут быть разделены пробелом.
- Например, домен [-2, 10) U (10, 2] включает -2 и 2, но не включает номер 10.
- Всегда используйте круглые скобки, если вы используете символ бесконечности, ∞. Это потому, что бесконечность - это понятие, а не число.
Шаг 3. Постройте график квадратного уравнения
Квадратные уравнения образуют параболический график, указывающий либо вверх, либо вниз. Учитывая, что парабола будет бесконечно продолжаться наружу по оси x, область определения наиболее квадратичной функции - это все действительные числа. Другими словами, квадратное уравнение охватывает все значения x на числовой прямой, что делает его область определения р (символ для всех действительных чисел).
- Чтобы получить представление о функции, выберите любое значение x и вставьте его в функцию. Решение функции с этим значением x выдаст значение y. Эти значения x и y являются координатами (x, y) графика функции.
- Постройте эту координату и повторите процесс с другим значением x.
- Построение нескольких значений таким образом должно дать вам общее представление о форме квадратичной функции.
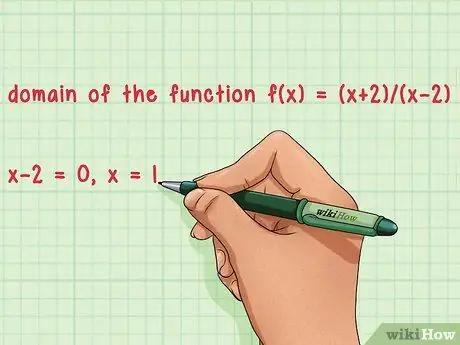
Шаг 4. Установите знаменатель равным нулю, если это дробь
Работая с дробью, нельзя делить на ноль. Установив знаменатель равным нулю и решив относительно x, вы можете вычислить значения, которые будут исключены в функции.
- Например: определить область определения функции f (x) = (х + 1)/(х - 1).
- Знаменатель этой функции равен (x - 1).
- Установите его равным нулю и решите относительно x: x - 1 = 0, x = 1.
- Запишите домен: домен этой функции не может включать 1, но включает все действительные числа, кроме 1; следовательно, область равна (-∞, 1) U (1, ∞).
- (-∞, 1) U (1, ∞) можно читать как набор всех действительных чисел, за исключением 1. Символ бесконечности ∞ представляет все действительные числа. В этом случае в домен включаются все действительные числа больше 1 и меньше единицы.

Шаг 5. Установите члены внутри радикала больше или равными нулю, если есть корневая функция
Вы не можете извлечь квадратный корень из отрицательного числа; следовательно, любое значение x, которое приводит к отрицательному числу, должно быть исключено из области определения этой функции.
- Например: определить область определения функции f (x) = √ (x + 3).
- Члены внутри радикала (x + 3).
- Установите их больше или равными нулю: (x + 3) ≥ 0.
- Решить относительно x: x ≥ -3.
- Область этой функции включает все действительные числа, большие или равные -3; следовательно, область равна [-3, ∞).
Часть 2 из 3: Нахождение диапазона квадратичной функции

Шаг 1. Подтвердите, что у вас есть квадратичная функция
Квадратичная функция имеет вид ax2 + bx + c: f (x) = 2x2 + 3x + 4. Форма квадратичной функции на графике - парабола, направленная вверх или вниз. Существуют разные методы вычисления диапазона функции в зависимости от типа, с которым вы работаете.
Самый простой способ определить диапазон других функций, таких как функции корня и дроби, - это нарисовать график функции с помощью графического калькулятора
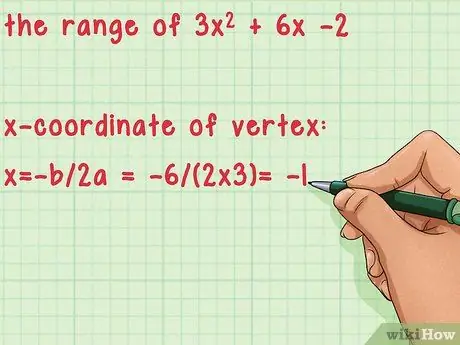
Шаг 2. Найдите значение x вершины функции
Вершиной квадратичной функции является вершина параболы. Помните, квадратное уравнение имеет вид топор2 + bx + c. Чтобы найти координату x, используйте уравнение x = -b / 2a. Это уравнение является производной основной квадратичной функции, которая представляет уравнение с нулевым наклоном (в вершине графика наклон функции равен нулю).
- Например, найдите диапазон 3x2 + 6x -2.
- Вычислить x-координату вершины: x = -b / 2a = -6 / (2 * 3) = -1
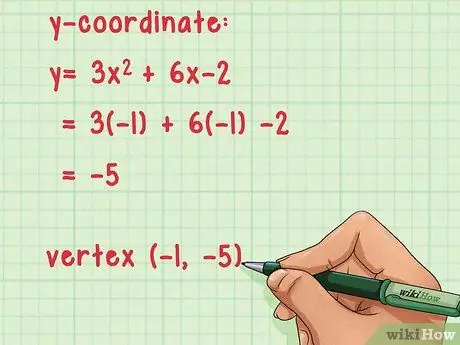
Шаг 3. Вычислить y-значение вершины функции
Подставьте координату x в функцию, чтобы вычислить соответствующее значение y вершины. Это значение y обозначает край вашего диапазона для функции.
- Вычислить координату y: y = 3x2 + 6x - 2 = 3 (-1)2 + 6(-1) -2 = -5.
- Вершина этой функции - (-1, -5).

Шаг 4. Определите направление параболы, подставив по крайней мере еще одно значение x
Выберите любое другое значение x и вставьте его в функцию, чтобы вычислить соответствующее значение y. Если значение y выше вершины, парабола продолжается до + ∞. Если значение y ниже вершины, парабола продолжается до -∞.
- Используйте значение x -2: y = 3x2 + 6х - 2 = у = 3 (-2)2 + 6(-2) - 2 = 12 -12 -2 = -2.
- Это дает координату (-2, -2).
- Эта координата говорит вам, что парабола продолжается выше вершины (-1, -5); следовательно, диапазон охватывает все значения y выше -5.
- Диапазон этой функции [-5, ∞)
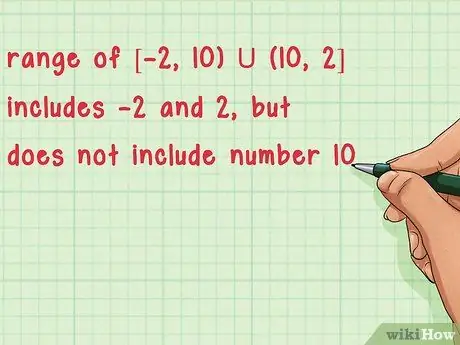
Шаг 5. Запишите диапазон в правильных обозначениях
Как и домен, диапазон записывается с той же нотацией. Используйте скобку, когда номер включен в домен, и скобку, если домен не включает номер. Буква U обозначает объединение, которое соединяет части домена, которые могут быть разделены пробелом.
- Например, диапазон [-2, 10) U (10, 2] включает -2 и 2, но не включает число 10.
- Всегда используйте круглые скобки, если вы используете символ бесконечности ∞.
Часть 3 из 3: Графическое определение диапазона функции

Шаг 1. Постройте график функции
Часто диапазон функции проще всего определить, просто построив ее график. Многие корневые функции имеют диапазон (-∞, 0] или [0, + ∞), потому что вершина боковой параболы находится на горизонтальной оси x. В этом случае функция охватывает все положительные значения y, если парабола идет вверх, или все отрицательные значения y, если парабола опускается. Функции дроби будут иметь асимптоты, определяющие диапазон.
- Некоторые корневые функции запускаются выше или ниже оси x. В этом случае диапазон определяется точкой, с которой запускается корневая функция. Если парабола начинается с y = -4 и идет вверх, то диапазон равен [-4, + ∞).
- Самый простой способ построить график функции - использовать графическую программу или графический калькулятор.
- Если у вас нет графического калькулятора, вы можете нарисовать грубый набросок графика, вставив значения x в функцию и получив соответствующие значения y. Нанесите эти координаты на график, чтобы получить представление о форме графика.
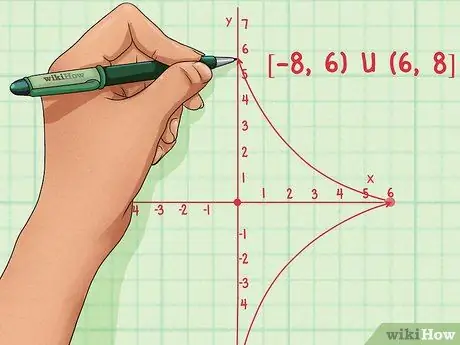
Шаг 2. Найдите минимум функции
После того, как вы построили график функции, вы сможете четко видеть самую нижнюю точку графика. Если очевидного минимума нет, знайте, что некоторые функции продолжат работу до -∞.
Функция дроби будет включать все точки, кроме тех, которые находятся в асимптоте. У них часто есть диапазоны, такие как (-∞, 6) U (6, ∞)

Шаг 3. Определите максимум функции
Опять же, после построения графика вы сможете определить максимальную точку функции. Некоторые функции продолжаются до + ∞ и, следовательно, не имеют максимума.

Шаг 4. Запишите диапазон в правильных обозначениях
Как и домен, диапазон записывается с той же нотацией. Используйте скобку, когда номер включен в домен, и скобку, если домен не включает номер. Буква U обозначает объединение, которое соединяет части домена, которые могут быть разделены пробелом.
- Например, диапазон [-2, 10) U (10, 2] включает -2 и 2, но не включает число 10.
- Всегда используйте круглые скобки, если вы используете символ бесконечности ∞.