Общеизвестно, что сумма всех внутренних углов треугольника равна 180 °, но откуда мы это знаем? Чтобы доказать, что сумма всех углов треугольника равна 180 градусам, вам необходимо понять некоторые общие геометрические теоремы. Используя некоторые из этих геометрических концепций, можно написать простое доказательство.
Шаги
Часть 1 из 2: Доказательство свойства суммы углов
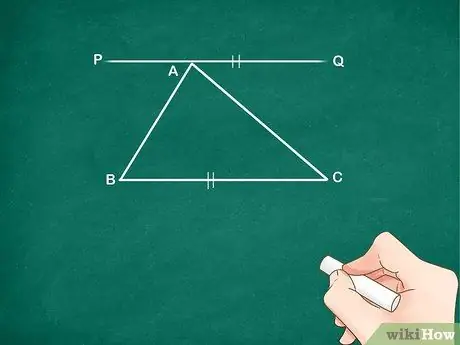
Шаг 1. Проведите линию, параллельную стороне BC треугольника, проходящую через вершину A
Обозначьте строку PQ. Постройте эту линию параллельно основанию треугольника.
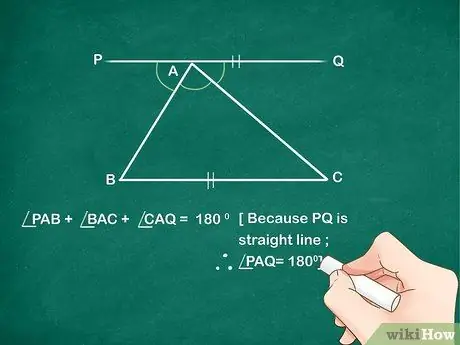
Шаг 2. Запишите уравнение: угол PAB + угол BAC + угол CAQ = 180 градусов
Помните, что все углы, составляющие прямую линию, должны быть равны 180 °. Поскольку угол PAB, угол BAC и угол CAQ вместе составляют линию PQ, их углы в сумме должны составлять 180 °. Назовите это уравнением 1.
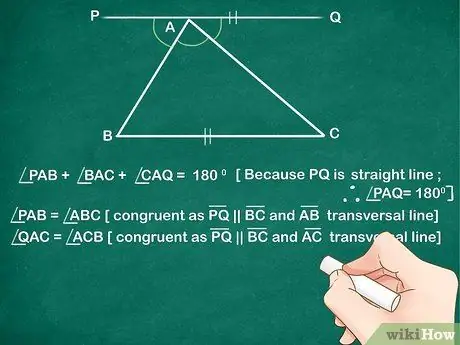
Шаг 3. Укажите, что угол PAB = угол ABC, а угол CAQ = угол ACB
Поскольку вы построили линию PQ параллельно стороне BC треугольника, альтернативные внутренние углы (PAB и ABC), образованные поперечной линией (линия AB), совпадают. Точно так же альтернативные внутренние углы (CAQ и ACB), образованные поперечной линией AC, также совпадают.
- Уравнение 2: угол PAB = угол ABC
- Уравнение 3: угол CAQ = угол ACB
- Это геометрическая теорема, согласно которой чередующиеся внутренние углы параллельных прямых совпадают.
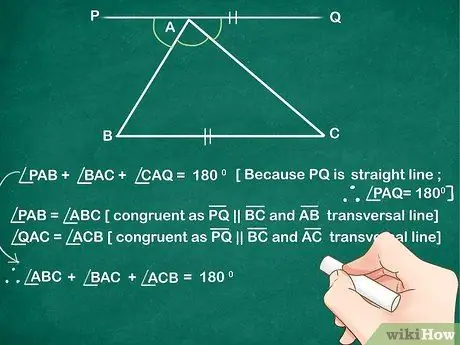
Шаг 4. Подставьте угол PAB и угол CAQ в уравнение 1 вместо угла ABC и угла ACB (как найдено в уравнении 2 и уравнении 3) соответственно
Зная, что альтернативные внутренние углы равны, вы можете заменить углы линии углами треугольника.
- Таким образом, мы получаем: Угол ABC + угол BAC + угол ACB = 180 °.
- Другими словами, в треугольнике ABC угол B + угол A + угол C = 180 °. Таким образом, сумма всех углов треугольника равна 180 °.
Часть 2 из 2: Понимание свойства суммы углов
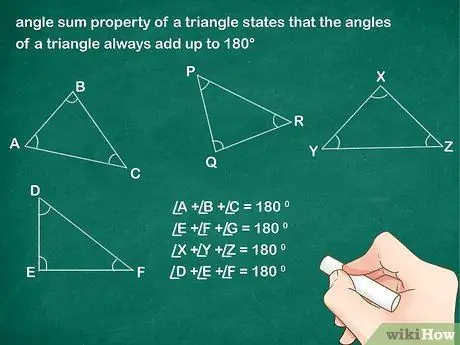
Шаг 1. Определите свойство суммы углов
Свойство суммы углов треугольника гласит, что сумма углов треугольника всегда равна 180 °. У каждого треугольника есть три угла, и будь то острый, тупой или прямоугольный треугольник, сумма углов равна 180 °.
- Например, в треугольнике ABC угол A + угол B + угол C = 180 °.
- Эта теорема полезна для нахождения неизвестного угла, когда вы знаете два других угла.
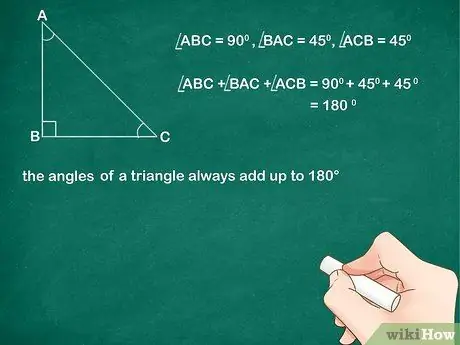
Шаг 2. Изучите примеры
Чтобы по-настоящему понять эту концепцию, может быть полезно изучить несколько примеров. Посмотрите на прямоугольный треугольник, в котором один из углов равен 90 °, а другие углы - по 45 °. Суммируем 90 ° + 45 ° + 45 ° = 180 °. Изучите другие треугольники разных форм и размеров и просуммируйте их углы. Вы увидите, что они всегда в сумме составляют 180 °.
Для примера прямоугольного треугольника: угол A = 90 °, угол B = 45 ° и угол C = 45 °. Теорема утверждает, что угол A + угол B + угол C = 180 °. Сложение углов дает 90 ° + 45 ° + 45 ° = 180 °. Следовательно, левая часть (L. H. S.) равна правой части (R. H. S.)

Шаг 3. Используйте теорему, чтобы найти неизвестный угол
Используя простую алгебру, вы можете использовать теорему о сумме углов, чтобы найти неизвестный угол, если вы знаете два других угла треугольника. Перепишите основное уравнение, чтобы найти неизвестный угол.
- Например, в треугольнике ABC угол A = 67 ° и угол B = 43 °, но угол C неизвестен.
- угол A + угол B + угол C = 180 °
- 67 ° + 43 ° + угол C = 180 °
- угол C = 180 ° - 67 ° - 43 °
- угол C = 70 °
