Невероятно, но все возвращается к Пифагору.
Одна из первых теорем, которую учат в математике, - это теорема Пифагора: если у вас есть прямоугольный треугольник, то квадрат наибольшей стороны (гипотенузы) всегда будет равен сумме квадратов катетов. две другие стороны. Первая целочисленная комбинация, для которой это работает, - это треугольник со сторонами 3, 4 и 5: ³² + ⁴²=⁵². Это работает и для других комбинаций чисел, в том числе:
- 5, 12 и 13,
- 6, 8 и 10,
- 7, 24 и 25,
и многое другое. Но 3, 4 и 5 особенные: это единственные последовательные целые числа, подчиняющиеся теореме Пифагора. Фактически, это единственные последовательные целые числа, которые вообще позволяют решить уравнение a² + b²=c². Но если бы вы позволили себе включить больше чисел, вы могли бы представить, что могут быть последовательные целые числа, которые подходят для более сложного уравнения, например, a² + b² + c²=d² + e ². Примечательно, что есть одно и только одно решение: 10² + 11² + 12²=13² + 14². Вот почему.
Один из самых глубоких способов взглянуть на теорему Пифагора - подумать о квадрате, который имеет определенную длину со всех сторон: назовем эту длину b. Площадь этого квадрата равна b ², потому что длина и ширина этого квадрата умножаются друг на друга. Если мы хотим сделать так, чтобы a ² + b ²=c ², и мы хотим, чтобы a, b и c были последовательными числами, то это накладывает огромные ограничения на a и c.
Это означает, что c должно быть равно (b + 1) и что a должно быть равно (b - 1), и это уравнение мы можем решить с помощью небольшой алгебры.
(b - 1)² + (b)²=(b + 1)², b ² - 2 b + 1 + b ²=b ² + 2 b + 1
b ² - 4 b=0.
И, следовательно, b должно быть равно 0 (что неинтересно) или 4, где 4 возвращает нам наше старое пифагорейское решение 3² + 4²=5².
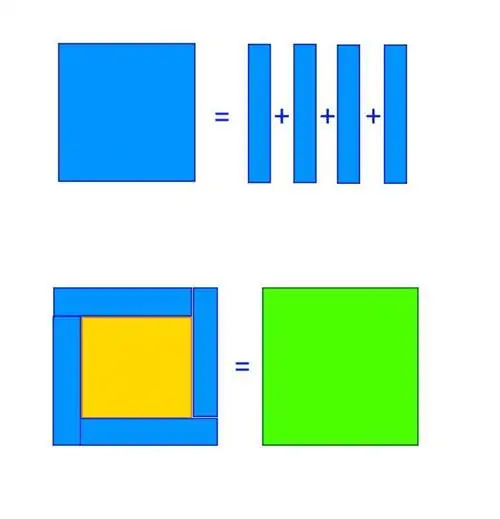
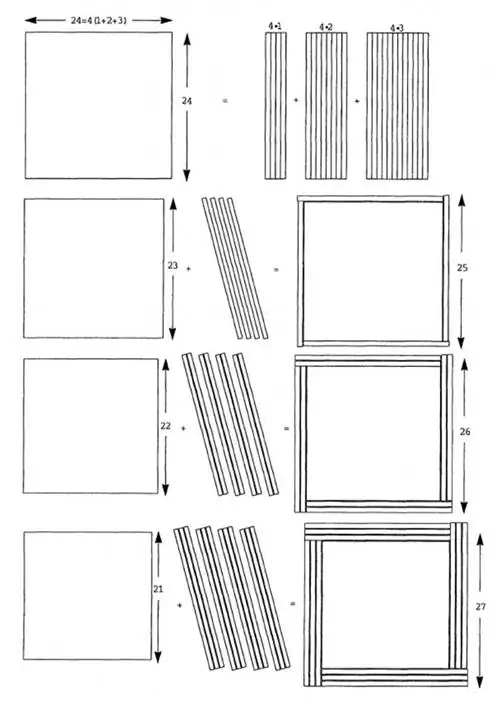
Но вы также можете решить это графически. Если вы начнете с квадрата, у которого b со всех сторон, то вы можете разбить его на линии, каждая из которых имеет толщину 1 единица. Поскольку у квадрата 4 стороны, единственный способ добавить эти линии к меньшему квадрату [это (b - 1) со всех сторон] и получить больший квадрат [это (b + 1) со всех сторон стороны] - если у вас есть 4 сегмента: по одному на каждую сторону.
На изображении выше ясно показано, как это сделать:
- вы разбиваете средний квадрат на b частей по 1 единице в каждой,
- вы складываете куски вокруг меньшего квадрата [размера a, который равен (b - 1)],
- и получить больший квадрат [размера c, который равен (c + 1)].
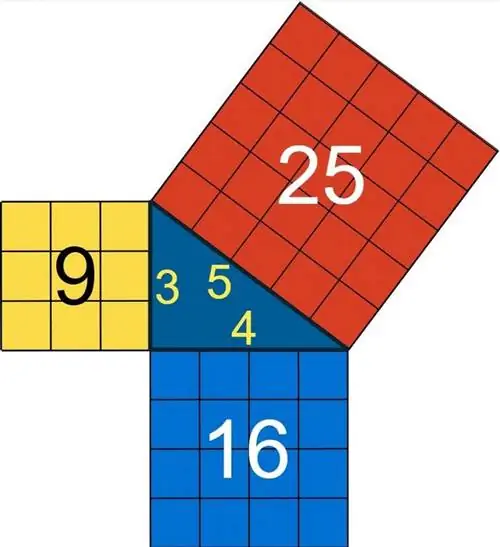
Это единственное решение для последовательных целых чисел, которое подходит для уравнения a ² + b ²=c ². Если вы сделаете свой квадрат среднего размера больше или меньше, у вас будет неправильное количество линий, которые нужно разместить вокруг меньшего квадрата, чтобы превратить его в больший квадрат; это просто невозможно сделать. Для a ² + b ²=c ² работают только последовательные целые числа 3, 4 и 5.
Но зачем ограничиваться только тремя номерами? Возможно, вы найдете последовательные целые числа, которые удовлетворяют этому типу отношения для любого нечетного числа последовательных целых чисел, например:
- a² + b²=c²,
- a² + b² + c²=d² + e ²,
- a² + b² + c² + d²=e ² + f² + g²,
и так далее.

На самом деле, если вы посмотрите на второй вариант, где a² + b² + c²=d² + e ², вы обнаружите, что работает одна и только одна комбинация чисел: 10² + 11² + 12²=13² + 14². Получается 100 + 121 + 144 слева, что в сумме дает 365, и 169 + 196 справа, что также дает в сумме 365.
Если бы вы хотели решить уравнения такого типа с помощью алгебры, вы все равно смогли бы это сделать, но это может занять некоторое время. В конце концов вы пришли бы к выводу, что среднее число c должно быть равно 12 (или 0, что опять же неинтересно), и поэтому полное уравнение, которое работает, будет 10² + 11² + 12²=13² + 14².
Но если бы мы вернулись к тому же графическому подходу, что и ранее, мы могли бы найти решение удивительно интуитивным способом.
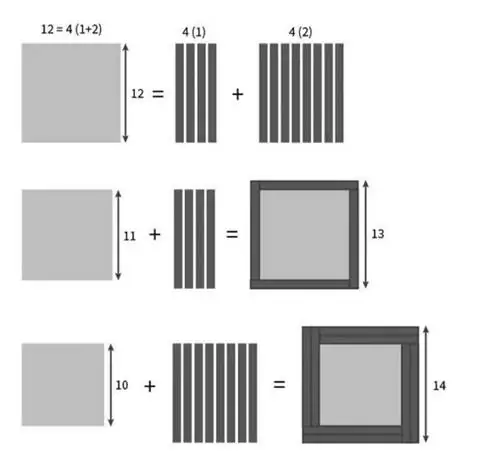
Как и раньше, мы возьмем средний «квадрат» (где все его стороны имеют длину c) и разобьем его на линии толщиной в 1 единицу. Однако, в отличие от первого раза, когда мы проделали этот трюк, на этот раз у нас есть два квадрата, которые нам нужно превратить в квадраты большего размера, используя эти линии:
- превращение меньшего квадрата [где его стороны равны (c - 1)] в больший квадрат [все стороны которого (c + 1)], и
- превращение еще меньшего квадрата [все стороны которого равны (c - 2)] на еще больший квадрат [все стороны которого равны (c + 2)].
Чтобы сделать это для первого квадрата, как и в прошлый раз, нам нужно всего четыре линии толщиной в 1 единицу. Но чтобы сделать это для второго квадрата, нам нужны четыре линии толщиной 2 единицы.
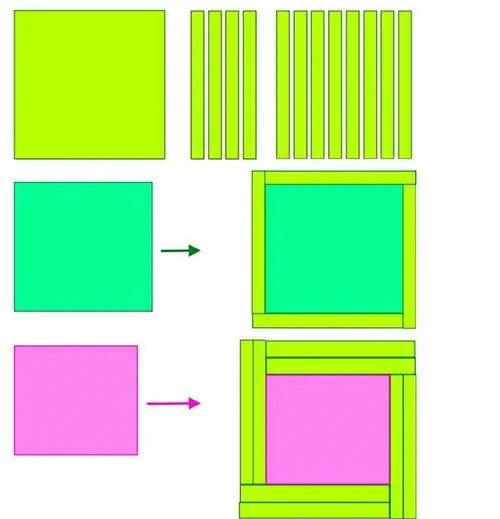
В общем, это работает, только если толщина этого среднего «квадрата» составляет 12 единиц толщины, и поэтому мы получаем уравнение 10² + 11² + 12²=13² + 14². Если у вас есть линия, состоящая из 12 единиц на 1 единицу, то вы можете взять четыре из них (4 × 12=48) и преобразовать 11² в 13², поскольку 121 + 48=169. Точно так же вы можете взять восемь таких строк (8 × 12=96), и преобразуйте 10² в 14², так как 100 + 96=196. Это единственное решение уравнения a² + b² + c²=d² + e ² для последовательных целых чисел.
В этот момент вы можете начать видеть появление шаблона, который всегда интересен с математической точки зрения. Мы сможем увидеть это гораздо яснее, если сделаем следующий шаг и спросим, каким будет решение для продолжения этого уравнения, включающего еще больше чисел.
Другими словами, как найти решение уравнения a² + b² + c² + d²=e ² + f² + g²?
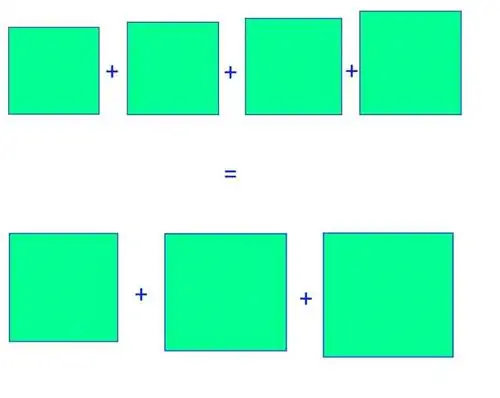
Если применить аналогичный подход, то теперь есть три меньших квадрата, которые нам нужно превратить в большие:
- квадрат со сторонами (d - 1) должен превратиться в квадрат со сторонами (d + 1), требующий четырех единиц длины d,
- квадрат со сторонами (d - 2) должен превратиться в квадрат со сторонами (d + 2), требующий восьми единиц длины d, и
- квадрат со сторонами (d - 3) должен превратиться в квадрат со сторонами (d + 3), требующий двенадцати единиц длины d.
Учитывая, что нам нужно, чтобы средний «квадрат» имел длину 4 + 8 + 12=24, это дает нам то, что, как мы подозреваем, должно быть нашим решением этого уравнения. Если это так, то 21² + 22² + 23² + 24²=25² + 26² + 27². Когда мы делаем математику, мы видим, что это дает нам 441 + 484 + 529 + 576=625 + 676 + 729, что подтверждается. Обе стороны равны 2030, то есть они равны друг другу.
В математике для этих типов последовательностей есть специальное название, восходящее к теореме Пифагора и исходному решению 3² + 4²=5²: пифагорейские последовательности. Паттерн, который возник для того, что представляет собой среднее число в последовательности, сохраняется до бесконечности: 4, 12, 24, 40, 60, 84, 112 и т. д. Итак, если вы хотите узнать, какие следующие последовательности чисел удовлетворяют этим типам уравнений, вы получите:
- 36² + 37² + 38² + 39² + 40²=41² + 42² + 43² + 44²,
- 55² + 56² + 57² + 58² + 59² + 60²=61² + 62² + 63² + 64² + 65²,
- 78² + 79² + … + 83² + 84²=85² + 86² + … + 89² + 90²,
и так далее. То, что выглядит диким математическим совпадением, на самом деле имеет глубокое, но простое объяснение.
В (невисокосном) году 365 дней, и 10² + 11² + 12²=13² + 14²=365. Однако этот математический факт не имеет ничего общего с нашим календарем в все, ни с вращением нашей планеты и обращением вокруг Солнца. Наоборот, количество дней в году здесь чистое совпадение, а математическое соотношение - прямое следствие пифагорейской геометрии, которую гораздо легче визуализировать, чем просто алгебру.
Пифагор только что начал с ² + b²=c ², в котором 3, 4 и 5 являются единственным набором последовательных чисел, которые решают эту задачу. Однако мы можем расширять это сколь угодно долго, и для каждого уравнения с нечетным числом членов, которое мы можем записать, существует только одно уникальное решение последовательных целых чисел. Эти пифагорейские прогоны имеют продуманную математическую структуру, и, поняв, как работают квадраты, мы можем понять, почему они не могут вести себя иначе.
