Определение квадратных дюймов (также записывается как в2) в любой двумерной области обычно довольно простой процесс. В простейших случаях, когда рассматриваемая площадь имеет форму квадрата или прямоугольника, площадь в квадратных дюймах определяется уравнением ширина × длина.
Площадь других форм (кругов, треугольников и т. Д.) Можно вычислить с помощью множества специализированных математических уравнений. При необходимости вы также можете легко преобразовать квадратные дюймы из квадратных футов или квадратных сантиметров.
Шаги
Метод 1 из 3: определение квадратных дюймов в квадрате или прямоугольнике
Шаг 1. Определите длину измеряемого участка
Квадраты и прямоугольники имеют четыре прямые стороны - в случае прямоугольников противоположные стороны имеют равную длину, а в случае квадратов все четыре стороны равны. Измерьте любую из сторон квадрата или прямоугольника, чтобы найти значение длины.
Шаг 2. Определите ширину измеряемой области
Затем измерьте любую из сторон, которые касаются той стороны, длину которой вы только что измерили. Эта сторона должна встречаться с первой под углом 90 градусов. Второе измерение - это ширина вашего квадрата или прямоугольника.
Поскольку все четыре стороны квадрата равны, величина "длины", полученная для квадрата, будет идентична измерению "ширины". В этом случае вам нужно измерить только одну сторону
Шаг 3. Умножьте длину на ширину
Просто умножьте свои измерения на длину и ширину, чтобы определить площадь вашего квадратного или прямоугольного участка в квадратных дюймах.
- Например, предположим, что для прямоугольной области вы измеряете длину 4 дюйма и ширину 3 дюйма. В этом случае площадь внутри вашего прямоугольника равна 4 × 3 = 12 квадратных дюймов.
- В случае с квадратами, поскольку все четыре стороны одинаковы, вы можете просто взять размер одной стороны и умножить его на себя (также называемое «возведение в квадрат» или принятие его во второй степени), чтобы получить значение в квадратных дюймах для площадь.
Метод 2 из 3: определение квадратных дюймов в других формах
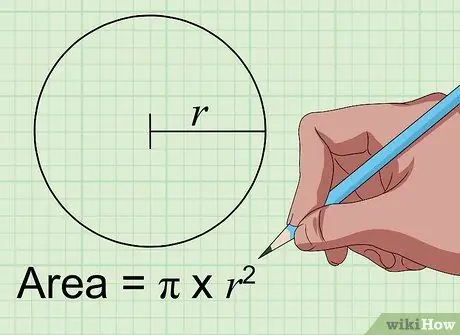
Шаг 1. Найдите площадь круга с помощью уравнения Area = pi × r.2.
Чтобы найти площадь круга в квадратных дюймах, все, что вам нужно знать, - это расстояние от центра круга до его края в дюймах. Это расстояние называется радиусом круга. Как только вы найдете это число, просто замените его на "r" в приведенном выше уравнении. Умножьте его на себя, затем умножьте на математическую константу «пи» (3,1415926…), чтобы определить квадратные дюймы внутри круга.
Итак, круг с радиусом 4 дюйма будет иметь площадь 50,27 квадратных дюйма, так как это произведение 3,14 x 16
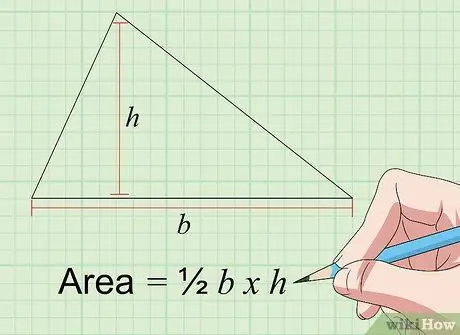
Шаг 2. Найдите площадь треугольника с помощью уравнения Площадь = 1/2 b × h
Площадь треугольника в квадратных дюймах определяется умножением его основания («b») на его высоту («h»), причем оба измерения в дюймах. Основание треугольника - это просто длина одной из его сторон, а его высота - это расстояние от стороны «основания» до противоположного угла при измерении под углом 90 градусов от стороны «основания». Площадь треугольника можно рассчитать, измерив основание и высоту для любой из трех его сторон и противоположного угла.
Следовательно, если вы выберете основную сторону длиной 4 дюйма, а соответствующая высота - 3 дюйма, ваш результат будет 2 x 3 = 6 квадратных дюймов
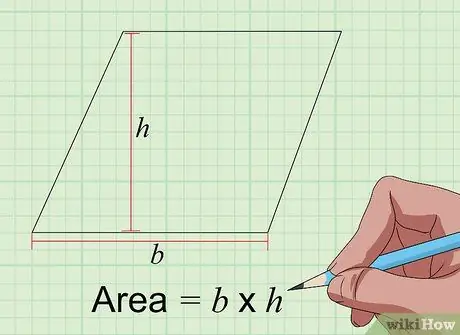
Шаг 3. Найдите площадь параллелограмма с помощью уравнения Площадь = b × h
Параллелограммы похожи на прямоугольники, с той лишь разницей, что их углы не обязательно пересекаются под углом 90 градусов. Соответственно, способ вычисления площади параллелограмма в квадратных дюймах аналогичен способу вычисления площади прямоугольника - просто умножьте основание параллелограмма на его высоту с обоими измерениями в дюймах. Его основание - это длина одной из его сторон, а его высота - это расстояние от противоположной стороны до первой стороны при измерении под прямым углом.
Таким образом, если длина выбранной стороны составляет 5 дюймов, а высота - 4 дюйма, результирующая площадь будет 5 x 4 = 20 квадратных дюймов
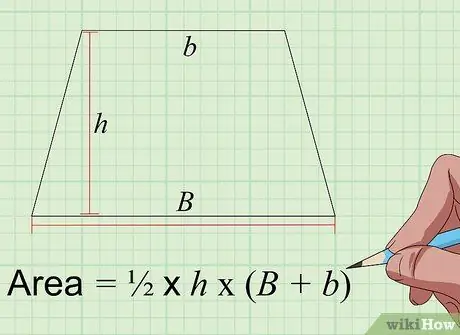
Шаг 4. Найдите площадь трапеции с помощью уравнения Площадь = 1/2 × h × (B + b)
Трапеция - это четырехсторонняя форма с одним набором параллельных сторон и одним набором непараллельных сторон. Чтобы рассчитать ее площадь в квадратных дюймах, необходимо выполнить три измерения (в дюймах): длину более длинной параллельной стороны («B»), длину более короткой параллельной стороны («b») и высоту трапеции (« h ) - расстояние между двумя параллельными сторонами, измеренное под прямым углом. Сложите длины двух сторон вместе, умножьте это на высоту, затем разделите результат пополам, чтобы найти площадь трапеции в квадратных дюймах.
Итак, если длинная сторона вашей трапеции составляет 6 дюймов, короткая сторона - 4 дюйма, а высота - 5 дюймов, результат будет ½ x 5 x (6 + 4) = 25 квадратных дюймов
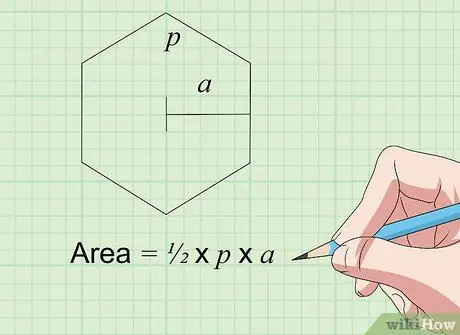
Шаг 5. Найдите площадь шестиугольника с помощью уравнения Площадь = ½ × P × a
Эта формула работает для любого правильного шестиугольника, что означает, что у него 6 равных сторон и 6 равных углов. P представляет собой периметр или 6-кратную длину одной стороны (6 x s) для правильного шестиугольника. a представляет апофему - длину от центра шестиугольника до середины любой одной стороны (то есть на полпути между любыми двумя углами). Умножьте их и уменьшите вдвое результат, чтобы определить площадь.
Таким образом, если у вашего шестиугольника 6 равных сторон по 4 дюйма каждая (что означает P = 6 x 4 = 24) и апофема 3,5 дюйма, расчет будет ½ x 24 x 3,5 = 42 квадратных дюйма
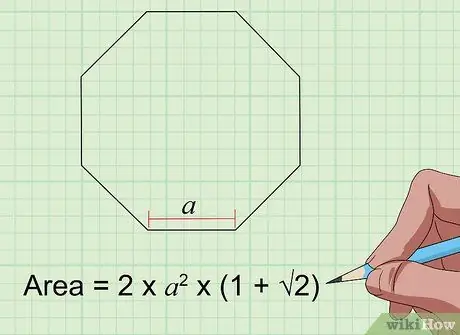
Шаг 6. Найдите площадь восьмиугольника с помощью уравнения Area = 2a² × (1 + √2)
Для правильного восьмиугольника (у которого 8 равных сторон и 8 равных углов) вам нужно знать только длину одной стороны («a» в формуле), чтобы определить площадь. Подставьте это измерение в формулу, и вы получите результат.
Следовательно, если у вашего обычного восьмиугольника длина стороны 4 дюйма, вы должны вычислить 2 (16) x (1 + 1,4) = 32 x 2,4 = 76,8 квадратных дюйма
Метод 3 из 3: преобразование в квадратные дюймы

Шаг 1. Преобразуйте ваши измерения в дюймы, прежде чем производить расчеты
Чтобы получить окончательный ответ в квадратных дюймах, проще всего указать любые измерения, необходимые для формулы (например, длину, высоту или апофему) в дюймах. Итак, если стороны вашего квадрата составляют 1 фут каждая, преобразуйте это в 12 дюймов, прежде чем производить расчет площади. Вот коэффициенты пересчета для общепринятых единиц измерения:
- 1 фут = 12 дюймов
- 1 ярд = 36 дюймов
- 1 сантиметр = 0,3937 дюйма
- 1 метр = 39,3701 дюйма
- 1 миллиметр = 0,0394 дюйма
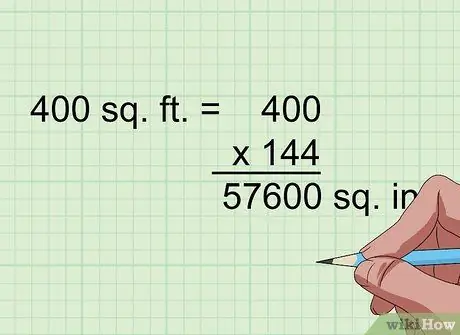
Шаг 2. Умножьте на 144, чтобы преобразовать квадратные футы в квадратные дюймы
1 квадратный фут - это буквально 1 фут в квадрате (или 1 фут умноженный на 1 фут); это означает, что это также 12 дюймов на 12 дюймов или 144 квадратных дюйма. Итак, если у вас есть площадь в квадратных футах, просто умножьте ее на 144, чтобы определить площадь в квадратных дюймах.
Например, 400 квадратных футов = 400 x 144 = 57600 квадратных дюймов
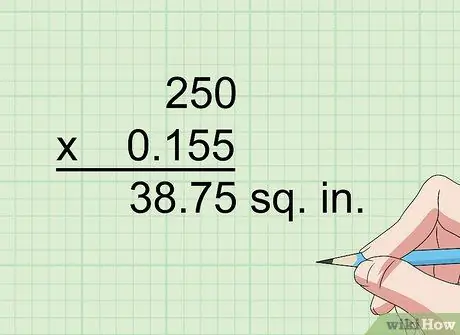
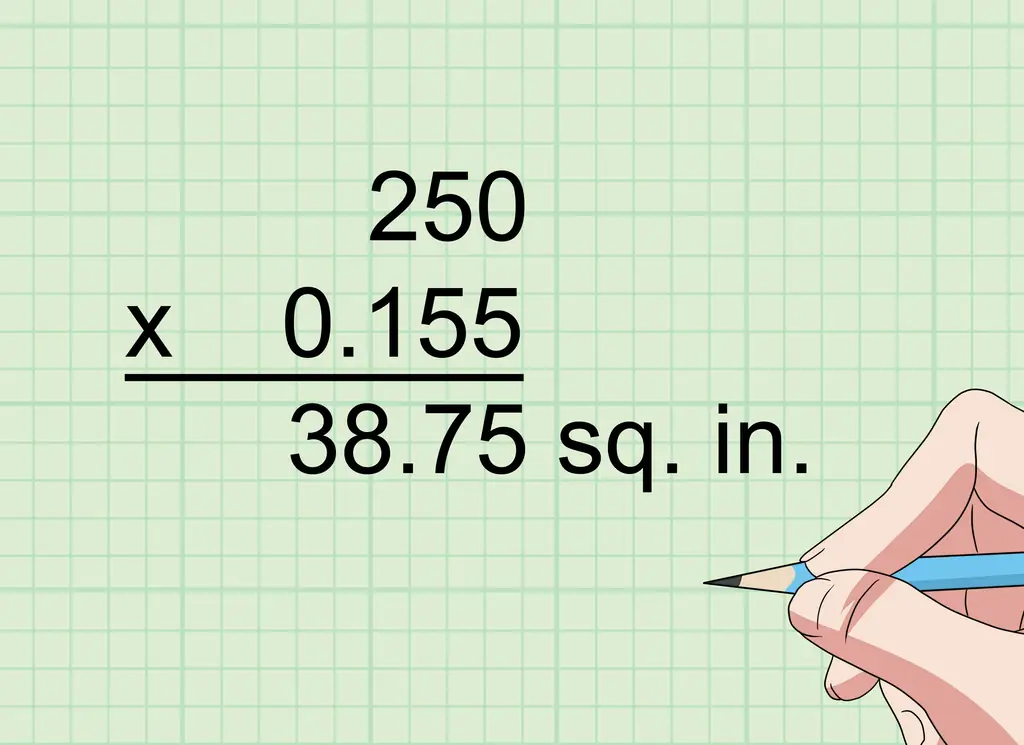
Шаг 3. Умножьте на 0,155, чтобы преобразовать квадратные сантиметры в квадратные дюймы
1 сантиметр равен примерно 0,394 дюйма, а 0,394 в квадрате (0,394 x 0,394) равняется 0,155. Таким образом, если вам нужно преобразовать результат в 250 квадратных сантиметров, умножьте 250 на 0,155, чтобы получить 38,75 квадратных дюймов.