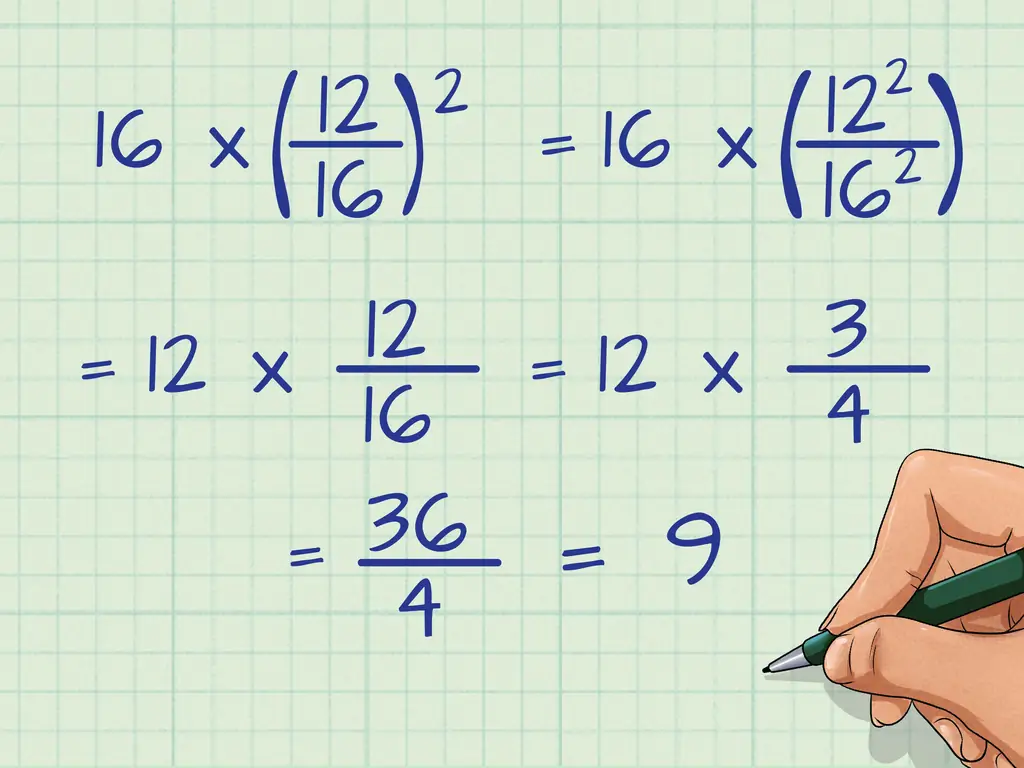Возведение дробей в квадрат - одна из самых простых операций, которые вы можете выполнять с дробями. Это очень похоже на возведение целых чисел в квадрат, поскольку вы просто умножаете числитель и знаменатель на себя. Есть также некоторые случаи, когда упрощение дроби перед возведением в квадрат упрощает процесс. Если вы еще не освоили этот навык, в этой статье представлен простой обзор, который быстро улучшит ваше понимание.
Шаги
Часть 1 из 3: возведение дробей в квадрат
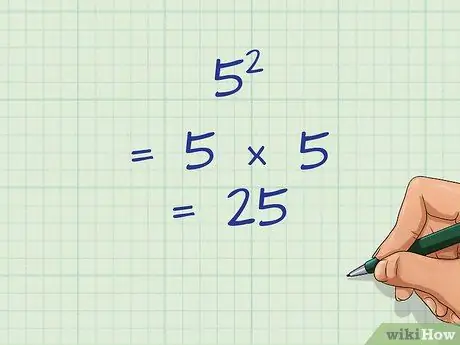
Шаг 1. Научитесь возводить целые числа в квадрат
Когда вы видите степень двойки, вы знаете, что вам нужно возвести это число в квадрат. Чтобы возвести в квадрат целое число, вы умножаете его само на себя. Например:
52 = 5 × 5 = 25
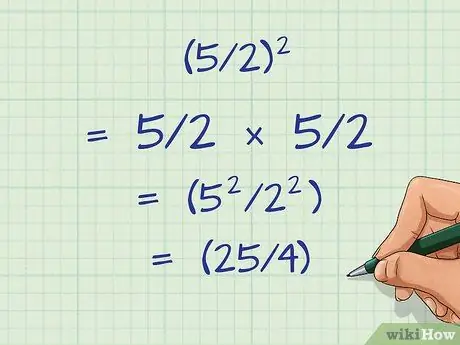
Шаг 2. Осознайте, что возведение дробей в квадрат работает точно так же
Чтобы возвести дробь в квадрат, вы умножаете дробь на себя. Другой способ подумать об этом - умножить числитель на себя, а затем знаменатель на себя. Например:
- (5/2)2 = 5/2 × 5/2 или (52/22).
- Возведение каждого числа в квадрат дает (25/4).
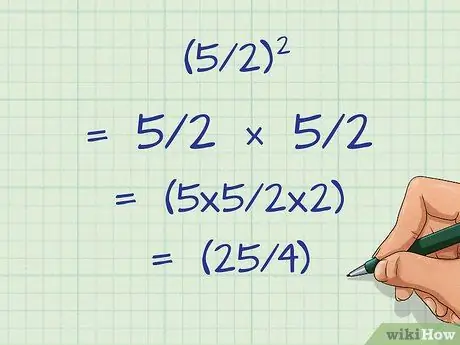
Шаг 3. Умножьте числитель на себя и знаменатель на себя
Фактический порядок, в котором вы умножаете эти числа на себя, не имеет значения, если вы возведете оба числа в квадрат. Для простоты начните с числителя: просто умножьте его на себя. Затем умножьте знаменатель на себя.
- Числитель останется вверху дроби, а знаменатель останется внизу дроби.
- Например: (5/2)2 = (5 х 5/2 х 2) = (25/4).
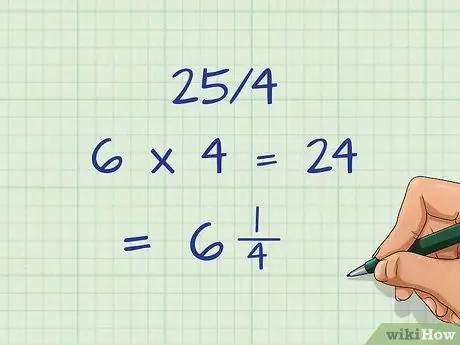
Шаг 4. Упростите дробь до конца
При работе с дробями последним шагом всегда является уменьшение дроби до ее наиболее простого вида или превращение неправильной дроби в смешанное число. В нашем примере 25/4 является неправильной дробью, потому что числитель больше знаменателя.
Чтобы преобразовать в смешанное число, разделите 4 на 25. Получается 6 раз (6 x 4 = 24) с 1 остатком. Следовательно, смешанное число - 6. 1/4.
Часть 2 из 3: возведение дробей в квадрат с отрицательными числами
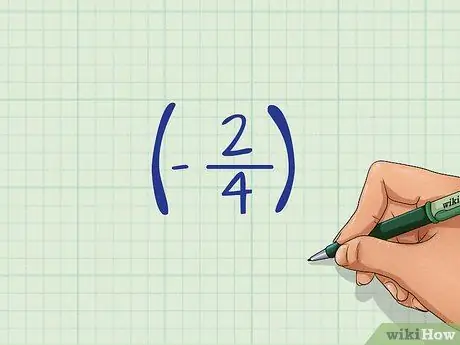
Шаг 1. Распознайте отрицательный знак перед дробью
Если вы работаете с отрицательной дробью, перед ней будет знак минус. Хорошей практикой является всегда заключать отрицательное число в круглые скобки, чтобы вы знали, что знак «-» относится к числу и не говорит вам вычесть два числа.
Например: (-2/4)
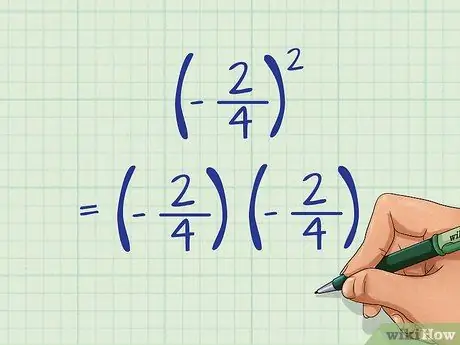
Шаг 2. Умножьте дробь на себя
Возведите дробь в квадрат, как обычно, умножив числитель на себя, а затем умножив знаменатель на себя. Как вариант, вы можете просто умножить дробь на себя.
Например: (-2/4)2 = (-2/4) Икс (-2/4)
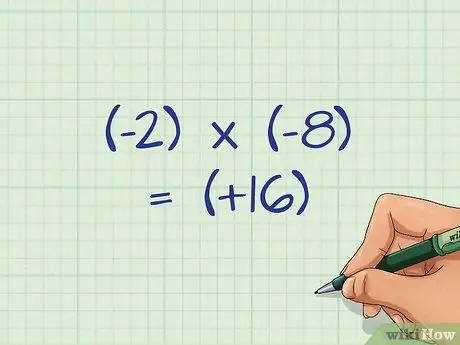
Шаг 3. Поймите, что два отрицательных числа умножаются, чтобы получить положительное число
Когда присутствует знак минус, вся дробь отрицательна. Когда вы возводите дробь в квадрат, вы умножаете два отрицательных числа вместе. Когда два отрицательных числа умножаются вместе, получается положительное число.
Например: (-2) x (-8) = (+16)
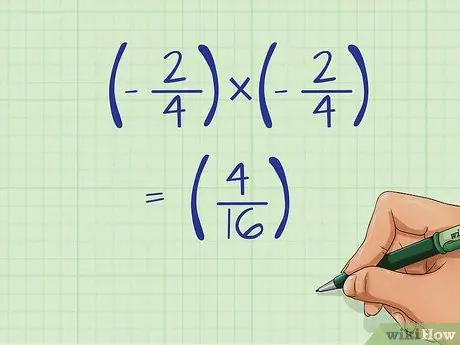
Шаг 4. Удалите отрицательный знак после возведения в квадрат
После того, как вы возведете дробь в квадрат, вы умножите два отрицательных числа. Это означает, что дробь в квадрате будет положительной. Обязательно напишите окончательный ответ без знака «минус».
- Продолжая пример, полученная дробь будет положительным числом.
- (-2/4) Икс (-2/4) = (+4/16)
- Обычно принято опускать знак «+» для положительных чисел.
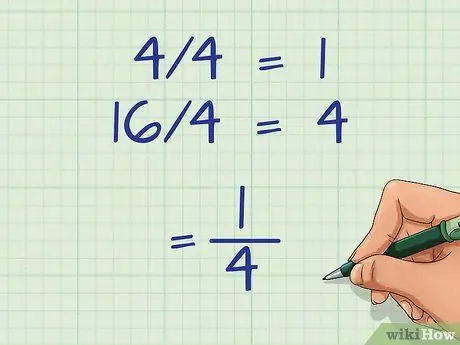
Шаг 5. Уменьшите дробь до простейшего вида
Последний шаг при выполнении любых вычислений с дробью - уменьшить ее. Неправильные дроби необходимо сначала преобразовать в смешанные числа, а затем уменьшить.
- Например: (4/16) имеет общий делитель четыре.
- Разделите дробь на 4: 4/4 = 1, 16/4 = 4
- Записываем упрощенную дробь: (1/4)
Часть 3 из 3: Использование упрощений и ярлыков
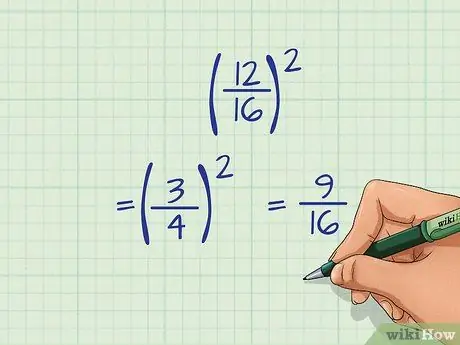
Шаг 1. Проверьте, можете ли вы упростить дробь, прежде чем возвести ее в квадрат
Обычно проще уменьшить дроби, прежде чем возводить их в квадрат. Помните, чтобы уменьшить дробь, нужно разделить ее на общий множитель до тех пор, пока число один не станет единственным числом, которое можно равномерно разделить как на числитель, так и на знаменатель. Уменьшение дроби в первую очередь означает, что вам не нужно уменьшать ее в конце, когда числа станут больше.
- Например: (12/16)2
- 12 и 16 можно разделить на 4. 12/4 = 3 и 16/4 = 4; следовательно, 12/16 сводится к 3/4.
- Теперь возведем дробь в квадрат 3/4.
- (3/4)2 = 9/16, который не может быть уменьшен.
-
Чтобы доказать это, возведем в квадрат исходную дробь без уменьшения:
- (12/16)2 = (12 х 12/16 х 16) = (144/256)
- (144/256) имеет общий множитель 16. Деление числителя и знаменателя на 16 уменьшает дробь до (9/16), ту же долю, которую мы получили от сокращения в первую очередь.

Шаг 2. Научитесь распознавать, когда вам следует подождать, чтобы уменьшить дробь
При работе с более сложными уравнениями вы можете просто отменить один из факторов. В этом случае действительно легче подождать, прежде чем уменьшать дробь. Добавление дополнительного фактора к приведенному выше примеру иллюстрирует это.
- Например: 16 × (12/16)2
- Разверните квадрат и вычеркните общий множитель 16: 16 * 12/16 * 12/16
Поскольку в знаменателе стоит одно целое число 16 и два целых числа 16, вы можете вычеркнуть ОДНО из них
- Перепишем упрощенное уравнение: 12 × 12/16
- Уменьшать 12/16 разделив на 4: 3/4
- Умножить: 12 × 3/4 = 36/4
- Разделить: 36/4 = 9
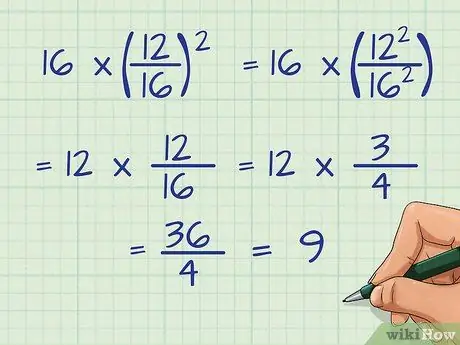
Шаг 3. Узнайте, как использовать ярлык для экспоненты
Другой способ решить тот же пример - сначала упростить показатель степени. Конечный результат такой же, это просто другой способ решения.
- Например: 16 * (12/16)2
- Записываем, возведя числитель и знаменатель в квадрат: 16 * (122/162)
- Вычеркнем показатель в знаменателе: 16 * 122/162
Представьте, что у первых 16 показатель степени 1:16.1. Используя правило экспоненты деления чисел, вы вычитаете экспоненты. 161/162, дает 161-2 = 16-1 или 1/16.
- Теперь вы работаете с: 122/16
- Перепишите и уменьшите дробь: 12*12/16 = 12 * 3/4.
- Умножить: 12 × 3/4 = 36/4
- Разделить: 36/4 = 9