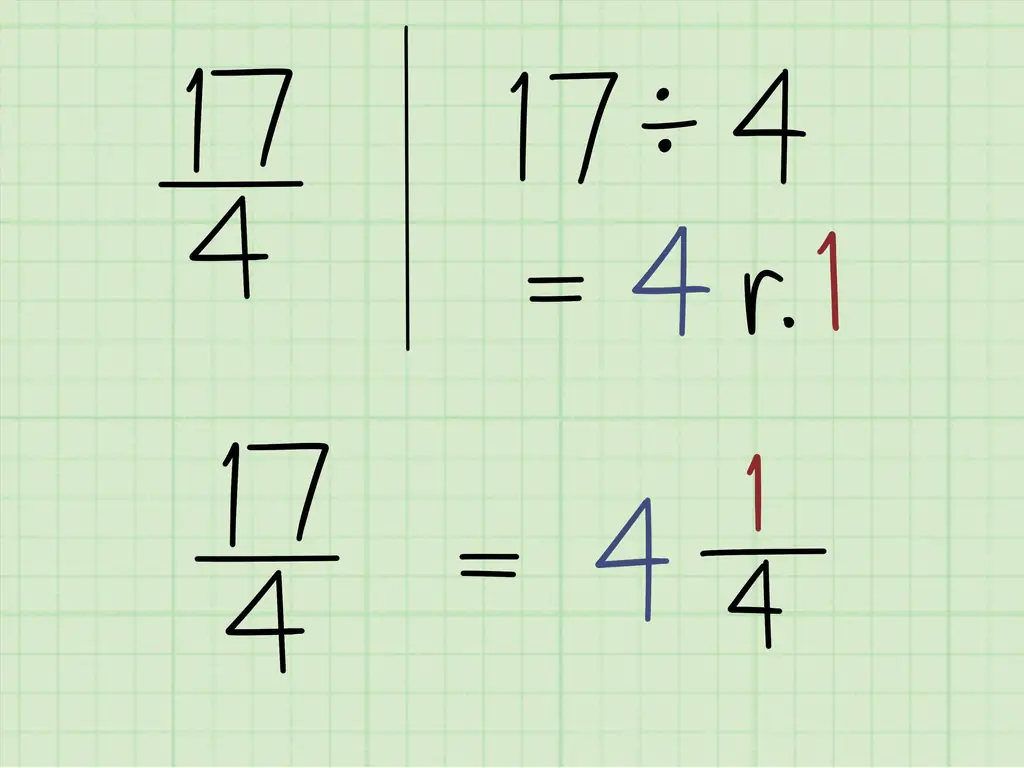Поначалу вопросы на дроби могут показаться сложными, но с практикой и ноу-хау они становятся проще. Начните с изучения терминологии и основ, затем начните складывать, вычитать, умножать и делить дроби. Как только вы поймете, что такое дроби и как ими манипулировать, вы быстро решите проблемы с дробями.
Шаги
Метод 1 из 2: вычисления с дробями

Шаг 1. Сложите дроби с одинаковым знаменателем, сложив числители
Чтобы сложить дроби, у них должен быть одинаковый знаменатель. Если да, просто сложите числители вместе.
Например, чтобы решить 5/9 + 1/9, просто прибавьте 5 + 1, что равно 6. Ответ: 6/9, которое можно уменьшить до 2/3

Шаг 2. Вычтите дроби с одинаковым знаменателем путем вычитания числителей
Если вам нужно вычесть дроби, они должны иметь тот же знаменатель, как если бы вы их складывали. Все, что вам нужно сделать, это вычесть меньший числитель из большего числителя, чтобы решить проблему.
Например, чтобы решить 6/8 - 2/8, все, что вам нужно сделать, это отнять 2 из 6. Ответ - 4/8, которое можно уменьшить до 1/2

Шаг 3. Найдите общее кратное для сложения или вычитания дробей без одинакового знаменателя
Если у дробей разный знаменатель, вам нужно найти общее кратное для обоих знаменателей и преобразовать каждую дробь, чтобы у них был одинаковый знаменатель. Для этого умножьте числитель и знаменатель на число, которое преобразует его в общее кратное. Затем сложите или вычтите числители, чтобы найти ответ.
- Например, если вам нужно сложить 1/2 и 2/3, начните с определения общего кратного. В данном случае общее кратное равно 6, поскольку 2 и 3 можно преобразовать в 6. Чтобы превратить 1/2 в дробь со знаменателем 6, умножьте числитель и знаменатель на 3: 1 x 3 = 3 и 2. x 3 = 6, поэтому новая дробь равна 3/6. Чтобы превратить 2/3 в дробь со знаменателем 6, умножьте числитель и знаменатель на 2: 2 x 2 = 4 и 3 x 2 = 6, так что новая дробь будет 4/6. Теперь вы можете сложить числители: 3/6 + 4/6 = 7/6. Поскольку это неправильная дробь, вы можете преобразовать ее в смешанное число 1 1/6.
- С другой стороны, предположим, что вы работаете над проблемой 7/10 - 1/5. Общее кратное в этом случае равно 10, поскольку 1/5 можно преобразовать в дробь со знаминателем 10, умножив ее на 2: 1 x 2 = 2 и 5 x 2 = 10, так что новая дробь будет 2/10.. Вам вообще не нужно преобразовывать другую дробь. Просто вычтите 2 из 7, что составляет 5. Ответ 5/10, которое также можно уменьшить до 1/2.

Шаг 4. Перемножьте дроби поперёк
К счастью, умножить дроби довольно просто. Если дроби еще не находятся в наименьшем значении, уменьшите их. Затем все, что вам нужно сделать, это умножить числитель на числитель, а знаменатель на знаменатель.
Например, чтобы умножить 2/3 и 7/8, найдите новый числитель, умножив 2 на 7, что составляет 14. Затем умножьте 3 на 8, что равно 24. Следовательно, ответ будет 14/24, что может быть уменьшается до 7/12 путем деления числителя и знаменателя на 2
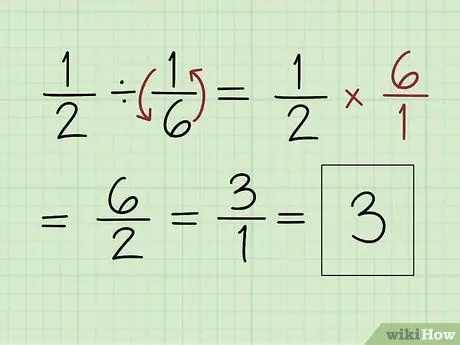
Шаг 5. Разделите дроби, переворачивая вторую дробь вверх дном и умножая прямо поперек
Чтобы разделить дроби, начните с деления дроби, которую вы хотите разделить, на обратную. Для этого переверните его так, чтобы числитель стал знаменателем, а знаменатель - числителем. Затем умножьте оба числителя и оба знаменателя вместе.
Например, чтобы решить 1/2 ÷ 1/6, переверните 1/6 вверх ногами, чтобы получилось 6/1. Затем просто умножьте 1 x 6, чтобы найти числитель (который равен 6), и 2 x 1, чтобы найти знаменатель (который равен 2). Итак, ответ - 6/2, что равно 3
Метод 2 из 2: Практика основ

Шаг 1. Обратите внимание, что числитель находится вверху, а знаменатель - внизу
Дроби относятся к частям целого, а верхнее число дроби называется числителем. Это говорит вам, со сколькими частями целого вы работаете. Нижнее число в дроби называется знаменателем и говорит вам, сколько частей составляет целое.
Например, в 3/5 3 - числитель, значит, 3 части, а 5 - знаменатель, значит, всего 5 частей. В 7/8 7 - числитель, а 8 - знаменатель

Шаг 2. Превратите целое число в дробь, поставив его над 1
Если у вас есть целое число и вам нужно преобразовать его в дробь, вы можете использовать целое число в качестве числителя. Всегда используйте 1 в качестве знаменателя, поскольку каждое неделимое целое состоит из одной части.
Например, если вам нужно превратить 7 в дробь, запишите это как 7/1
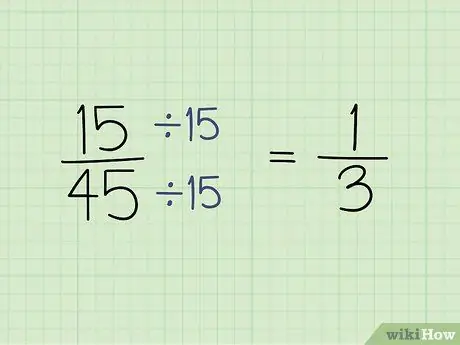
Шаг 3. Уменьшите дроби, если вам нужно их упростить
Начните с поиска наибольшего общего множителя числителя и знаменателя. GCF - это наибольшее число, на которое можно разделить как числитель, так и знаменатель. Затем просто разделите числитель и знаменатель на наибольший общий множитель, чтобы уменьшить дробь.
Например, если у вас дробь 15/45, наибольший общий множитель равен 15, поскольку и 15, и 45 можно разделить на 15. Разделите 15 на 15, что равно 1, и получится ваш новый числитель. Разделите 45 на 15, что равно 3, и получится ваш новый знаменатель. Это означает, что 15/45 можно уменьшить до 1/3
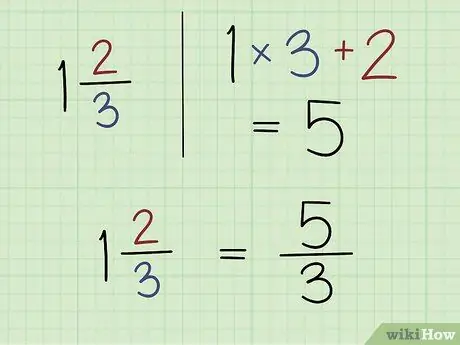
Шаг 4. Научитесь превращать смешанные числа в неправильные дроби
Смешанное число состоит из целого числа и дроби. Чтобы упростить решение некоторых вопросов о дробях, вам может потребоваться превратить смешанное число в неправильную дробь (это означает, что число вверху больше, чем число внизу). Вы можете сделать это, умножив целое число на знаменатель и прибавив это число к числителю. Поставьте новый числитель над знаменателем.
Допустим, у вас смешанное число 1 2/3. Начните, умножив 3 на 1, что составляет 3. Добавьте 3 к 2, существующему числителю. Новый числитель равен 5, поэтому смешанная дробь составляет 5/3
Кончик:
Как правило, вам нужно преобразовать смешанные числа в неправильные дроби, если вы их умножаете или делите.

Шаг 5. Придумайте, как преобразовать неправильные дроби в смешанные числа
Иногда у вас может возникнуть противоположная проблема, и вам нужно сделать неправильную дробь смешанным числом. Для начала выясните, сколько раз числитель может входить в знаменатель с помощью деления. Это становится вашим целым числом. Найдите остаток, умножив целое число на делитель (число, на которое вы делите) и вычтите результат из делимого (число, которое вы делите). Положите остаток над исходным знаменателем.
Скажите, что у вас неправильная дробь 17/4. Поставьте задачу как 17 ÷ 4. Число 4 переходит в 17 в общей сложности 4 раза, так что целое число равно 4. Затем умножьте 4 на 4, что равно 16. Вычтите 16 из 17, что равно 1, так что это остаток. Это означает, что 17/4 равно 4 1/4
подсказки
- Найдите время, чтобы внимательно прочитать проблему хотя бы дважды, чтобы быть уверенным, что вы знаете, что она просит вас сделать.
- Узнайте у своего учителя, нужно ли вам преобразовывать неправильные дроби в смешанные числа и / или сокращать дроби до наименьших значений, чтобы получить полные оценки.
- Чтобы получить обратное целое число, просто поставьте над ним 1. Например, 5 становится 1/5.
- Дроби никогда не могут иметь нулевой знаменатель. Нулевой знаменатель не определен, поскольку деление на ноль математически недопустимо.