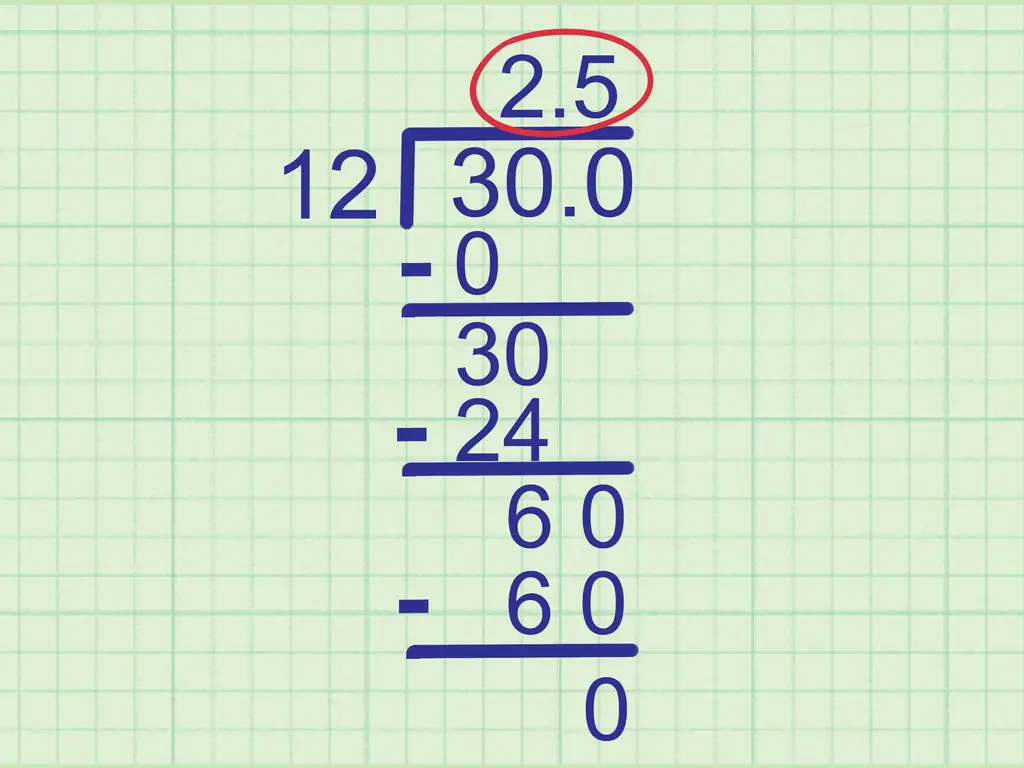Поначалу деление на десятичное число может показаться трудным. В конце концов, никто не учил вас «таблице умножения на 0,7». Секрет в том, чтобы преобразовать проблему деления в формат, в котором используются только целые числа. Как только вы переписываете задачу таким образом, она превращается в обычную задачу с долгим делением.
Шаги
Часть 1 из 2: Запись задачи как задачи обычного деления
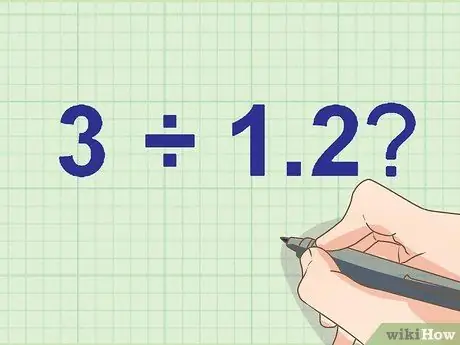
Шаг 1. Запишите задачу о делении
Используйте карандаш на случай, если вы захотите исправить свою работу.
-
Пример:
Что такое 3 ÷ 1.2?

Шаг 2. Запишите целое число в виде десятичной дроби
Запишите десятичную точку после целого числа, а затем запишите нули после десятичной точки. Делайте это до тех пор, пока оба числа не будут иметь одинаковое количество разрядов справа от десятичной точки. Это не меняет значения целого числа.
-
Пример:
В задаче 3 ÷ 1.2 наше целое число равно 3. Поскольку у 1.2 есть одна позиция справа от десятичной точки, перепишите 3 как 3.0, чтобы у него также было одно место после десятичной точки. Теперь наша проблема 3.0 ÷ 1.2.
- Предупреждение: не добавляйте нули слева от десятичной точки! 3 - это то же самое, что 3.0 или 3.00, но не то же самое, что 30 или 300.

Шаг 3. Перемещайте десятичные дроби вправо, пока не получите целые числа
В задачах деления вам разрешено перемещать десятичные точки, но только если вы перемещаете их на одинаковую величину для каждого числа. Это позволяет превратить проблему в целые числа.
-
Пример:
Чтобы преобразовать 3,0 ÷ 1,2 в целые числа, переместите десятичные знаки на одну позицию вправо. 3.0 становится 30, а 1.2 становится 12. Теперь наша проблема 30 ÷ 12.

Шаг 4. Напишите задачу в столбик
Поместите дивиденд (обычно большее число) под символом длинного деления. Запишите делитель вне его. Теперь у вас есть обычная задача деления в столбик с использованием целых чисел. Если вам нужно напоминание о том, как выполнять деление в столбик, прочтите следующий раздел.
Часть 2 из 2: Решение задачи о длинном делении

Шаг 1. Найдите первую цифру ответа
Начните решать это как обычно, сравнивая делитель с первой цифрой делимого. Вычислите, сколько раз делитель входит в эту цифру, затем запишите это число над этой цифрой.
Пример: Мы пытаемся уместить 12 в 30. Сравните 12 с первой цифрой делителя, 3. Поскольку 12 больше 3, оно входит в него 0 раз. Напишите 0 над цифрой 3 в строке ответа.
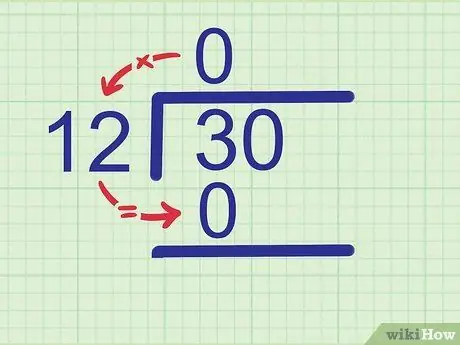
Шаг 2. Умножьте эту цифру на делитель
Напишите произведение (ответ на задачу умножения) под делимым. Запишите его прямо под первой цифрой делимого, так как это цифра, на которую вы только что смотрели.
-
Пример:
Поскольку 0 x 12 = 0, пишем 0 под 3.
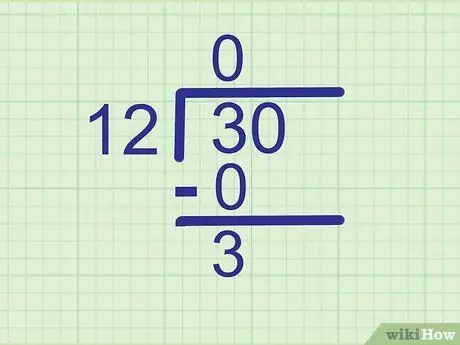
Шаг 3. Вычтите, чтобы найти то, что осталось
Вычтите продукт, который вы только что нашли, из цифры прямо над ним. Напишите ответ на новой строке ниже.
-
Пример:
3-0 = 3, поэтому напишите
Шаг 3. прямо под 0.
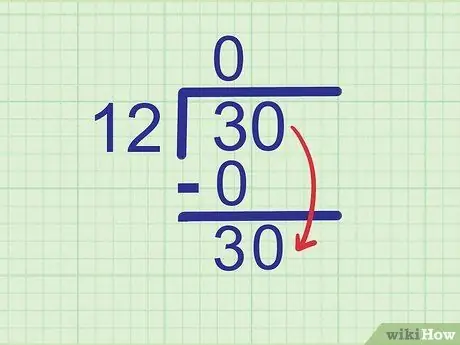
Шаг 4. Введите следующую цифру
Поместите следующую цифру делимого рядом с только что написанным числом.
-
Пример:
Наш дивиденд равен 30. Мы уже посмотрели на 3, поэтому следующая цифра, которую нужно опустить, - 0. Поместите ее рядом со своими 3, чтобы получить
Шаг 30..
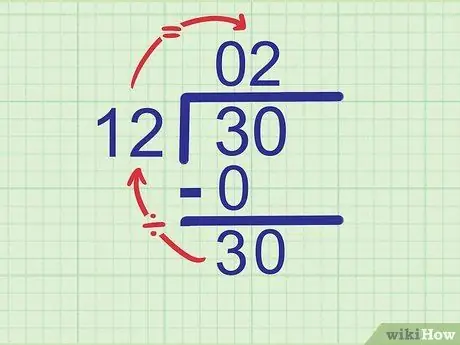
Шаг 5. Попробуйте вписать делитель в новое число
Теперь повторите первый шаг этого раздела, чтобы найти вторую цифру вашего ответа. На этот раз сравните делитель с числом, которое вы только что написали в самой нижней строке.
-
Пример: «Сколько раз 12 умещается в 30? Ближайшее значение, которое мы можем получить, равно 2, так как 12 x 2 = 24. Напишите
Шаг 2. во втором месте строки ответа.
- Если вы не знаете, каков ответ, попробуйте несколько задач на умножение, пока не найдете наиболее подходящий ответ. Например, если кажется, что 3 означает запись, умножьте 12 x 3, и вы получите 36. Это слишком много, так как мы пытаемся уместить в пределах 30. Попробуйте следующее: 12 x 2 = 24 Это подходит, так что 2 - правильный ответ.

Шаг 6. Повторите описанные выше шаги, чтобы найти следующий номер
Это тот же процесс длинного деления, который использовался выше, и для любой задачи длинного деления:
- Умножьте новую цифру в строке ответа на делитель: 2 x 12 = 24.
- Напишите продукт на новой строке под дивидендом: Напишите 24 прямо под 30.
- Вычтите самую низкую строку из предыдущей: 30-24 = 6, поэтому напишите 6 на новой строке ниже.

Шаг 7. Продолжайте, пока не дойдете до конца строки ответа
Если в вашем дивиденде осталась еще одна цифра, уменьшите ее и продолжайте решать проблему таким же образом. Если вы дошли до конца строки ответа, переходите к следующему шагу.
-
Пример:
Мы только что написали
Шаг 2. в конце строки ответа. Переходите к следующему шагу.

Шаг 8. Добавьте десятичную дробь, чтобы при необходимости увеличить дивиденд
Если числа разделены поровну, в вашей последней задаче на вычитание ответ будет «0». Это означает, что все готово, и у вас есть целое число в качестве ответа на вашу проблему. Но если вы дошли до конца строки ответа, а еще что-то осталось разделить, вам нужно увеличить делимое, добавив десятичную точку с последующим 0. Помните, это не меняет значения числа.
-
Пример:
Мы в конце строки ответа, но ответ на нашу последнюю задачу на вычитание - «6». Увеличьте цифру «30» под символом длинного деления, добавив «.0» в конец. Напишите десятичную точку в том же месте в строке ответа, но пока ничего не пишите после нее.

Шаг 9. Повторите те же шаги, чтобы найти следующую цифру
Единственная разница здесь в том, что вы должны переместить десятичную точку в одно и то же место в строке ответа. Как только вы это сделаете, поиск оставшихся цифр ответа будет таким же.
-
Пример:
Опустите новый 0 до последней строки, чтобы получилось «60». Поскольку 12 переходит в 60 ровно 5 раз, напишите
Шаг 5. как последняя цифра в нашей строке ответа. Не забывайте, что мы ставим десятичную дробь в нашу строку ответа, поэтому 2.5 это окончательный ответ на нашу проблему.
Видео - с помощью этой службы некоторая информация может быть передана YouTube
подсказки
- Если вы правильно следуете методу долгого деления, у вас всегда будет десятичная точка в правильном положении или вообще не будет десятичной точки, если числа делятся равномерно. Не пытайтесь угадать, куда идет десятичная дробь; это часто отличается от того, где десятичная дробь находится в числах, с которых вы начали.
- Вместо этого вы можете записать это как остаток (так что ответ на 3 ÷ 1,2 будет «2 остатка 6»). Но теперь, когда вы работаете с десятичными числами, ваш учитель, вероятно, ожидает, что вы также решите десятичную часть ответа.
- Если проблема с делением в столбик продолжается долгое время, вы можете в какой-то момент остановиться и округлить до ближайшего числа. Например, чтобы решить 17 ÷ 4,20, просто вычислите 4,047… и округлите ответ до «примерно 4,05».
-
Запомните условия вашего подразделения:
- Дивиденд - это число, которое делится.
- Делитель - это число, на которое вы делите.
- Частное - это решение математической задачи.
- Все вместе: Дивиденд ÷ Делитель = Частное.