Задачи двоичного деления могут быть решены с использованием длинного деления, которое является полезным методом для обучения процессу самого себя или написания простой компьютерной программы. В качестве альтернативы метод повторного вычитания с дополнением предоставляет подход, с которым вы, возможно, не знакомы, хотя он не так часто используется в программировании. Машинные языки обычно используют алгоритм оценки для большей эффективности, но здесь они не описываются.
Шаги
Метод 1 из 2: Использование длинного деления

Шаг 1. Проверьте десятичное деление в столбик
Если прошло некоторое время с тех пор, как вы делали столбики с обычными десятичными числами (с основанием десять), просмотрите основы, используя задачу 172 ÷ 4. В противном случае перейдите к следующему шагу, чтобы изучить тот же процесс в двоичном формате.
- В дивиденд делится на делитель, и ответ - частное.
- Сравните делитель с первой цифрой делимого. Если делитель является большим числом, продолжайте добавлять цифры к делимому, пока делитель не станет меньшим числом. (Например, при вычислении 172 ÷ 4 мы бы сравнили 4 и 1, заметили, что 4> 1, и вместо этого сравнили 4 с 17.)
- Напишите первую цифру частного над последней цифрой делимого, которую вы использовали при сравнении. Сравнивая 4 и 17, мы видим, что 4 четыре раза переходит в 17, поэтому мы пишем 4 как первую цифру нашего частного над 7.
- Умножьте и вычтите, чтобы найти остаток. Умножьте цифру частного на делитель, в данном случае 4 x 4 = 16. Запишите 16 под 17, затем вычтите 17-16, чтобы найти остаток, 1.
- Повторить. Еще раз, мы сравниваем делитель 4 со следующей цифрой 1, обратите внимание, что 4> 1, и «опускаем» следующую цифру делимого, чтобы вместо этого сравнить 4 с 12. 4 переходит в 12 трижды без остатка, поэтому мы пишем 3 как следующую цифру частного. Ответ - 43.

Шаг 2. Установите задачу двоичного деления в столбик
Давайте воспользуемся примером 10101 ÷ 11. Запишите это как задачу деления в столбик, с 10101 в качестве делимого и 11 в качестве делителя. Оставьте пространство вверху, чтобы написать частное, и внизу, чтобы записать свои расчеты.

Шаг 3. Сравните делитель с первой цифрой делимого
Это работает так же, как проблема с десятичным делением в столбик, но на самом деле это намного проще в двоичном формате. Либо вы не можете разделить число на делитель (0), либо делитель может идти за один раз (1):
11> 1, поэтому 11 не может «перейти в» 1. Запишите 0 как первую цифру частного (над первой цифрой делимого)
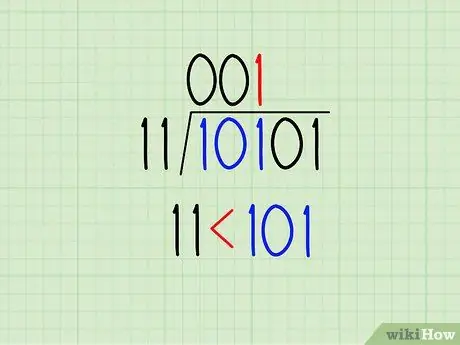
Шаг 4. Прикрепите следующую цифру и повторяйте, пока не получите 1
Вот пара следующих шагов к нашему примеру:
- Приведите следующую цифру делимого вниз. 11> 10. Напишите 0 в частном.
- Приведите следующую цифру вниз. 11 <101. Напишите 1 в частном.
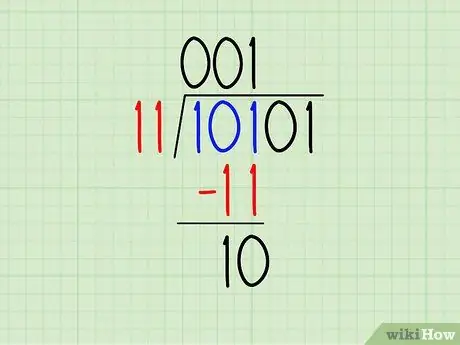
Шаг 5. Найдите остаток
Как и в случае десятичного деления в столбик, мы умножаем только что найденную цифру (1) на делитель (11) и записываем результат под нашим делимым, выровненным с цифрой, которую мы только что вычислили. В двоичном формате мы можем сократить это, поскольку 1 x делитель всегда равен делителю:
- Напишите делитель под дивидендом. Здесь мы пишем 11 с выравниванием под первыми тремя цифрами (101) делимого.
- Вычислите 101-11, чтобы получить остаток 10. Посмотрите, как вычесть двоичные числа, если вам нужен обзор.
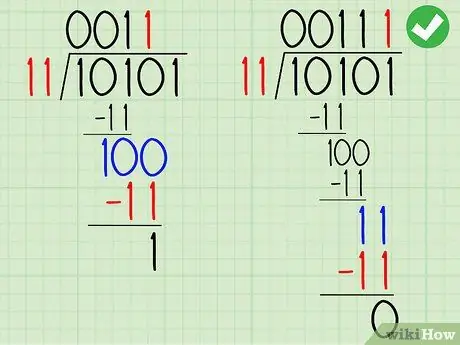
Шаг 6. Повторяйте, пока проблема не исчезнет
Приведите следующую цифру делителя к остатку, чтобы получилось 100. Поскольку 11 <100, запишите 1 в качестве следующей цифры частного. Продолжайте проблему, как и раньше:
- Напишите 11 под 100 и вычтите, чтобы получить 1.
- Опустите последнюю цифру делимого, чтобы получилось 11.
- 11 = 11, поэтому запишите 1 как последнюю цифру частного (ответа).
- Остатка нет, значит, проблема решена. Ответ 00111, или просто 111.
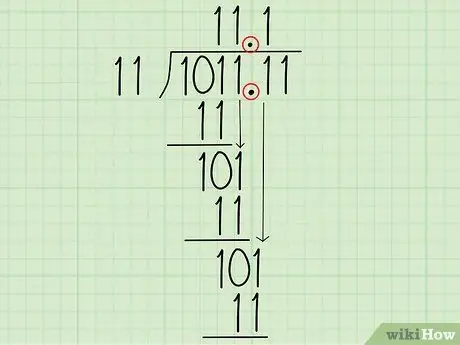
Шаг 7. При необходимости добавьте точку счисления
Иногда результат не является целым числом. Если у вас все еще есть остаток после использования последней цифры, добавьте «.0» к делимому и «.» к вашему частному, чтобы вы могли уменьшить еще одну цифру и продолжить. Повторяйте, пока не достигнете желаемой конкретности, а затем округлите ответ. На бумаге вы можете округлить в меньшую сторону, отрубив последний 0, или, если последняя цифра равна 1, отбросьте ее и добавьте 1 к новой последней цифре. В программировании следуйте одному из стандартных алгоритмов округления, чтобы избежать ошибок при преобразовании между двоичными и десятичными числами.
- Проблемы с двоичным делением часто заканчиваются повторением дробных частей чаще, чем в десятичной системе счисления.
- Это называется более общим термином «точка счисления», который применяется к любой системе счисления, поскольку «десятичная точка» используется только в десятичной системе счисления.
Метод 2 из 2: Использование метода дополнения

Шаг 1. Разберитесь в основной концепции
Один из способов решения проблем деления - в любом основании - состоит в том, чтобы продолжать вычитать делитель из делимого, а затем остаток, подсчитывая, сколько раз вы можете это сделать, прежде чем получите отрицательное число. Вот пример решения задачи 26 ÷ 7 по основанию десять:
- 26-7 = 19 (вычитаем 1 раз)
- 19 - 7 = 12 (2)
- 12 - 7 = 5 (3)
- 5-7 = -2. Отрицательное число, так что сделайте резервную копию. Ответ - 3 с остатком 5. Обратите внимание, что этот метод не вычисляет нецелую часть ответа.
Шаг 2. Научитесь вычитать с помощью дополнений
Хотя вы можете легко использовать описанный выше метод в двоичном формате, мы также можем использовать более эффективный метод вычитания, который экономит время при программировании компьютеров на деление двоичных чисел. Это метод вычитания с помощью дополнений в двоичном формате. Вот основы расчета 111 - 011 (убедитесь, что оба числа имеют одинаковую длину):
- Найдите дополнение до единиц второго члена, вычитая каждую цифру из 1. Это легко сделать в двоичной системе, переключая каждую 1 на 0 и каждую 0 на 1. В нашем примере 011 становится 100.
- Добавьте к результату единицу: 100 + 1 = 101. Это называется дополнением до двоек и позволяет нам выполнять вычитание как задачу сложения. По сути, результат такой, как если бы мы добавили отрицательное число вместо вычитания положительного, как только мы закончим процесс.
- Добавьте результат к первому члену. Напишите и решите задачу на сложение: 111 + 101 = 1100.
- Отбросьте цифру переноса. Отбросьте первую цифру вашего ответа, чтобы получить окончательный результат. 1100 → 100.
Шаг 3. Объедините две приведенные выше концепции
Теперь вы знаете метод вычитания для решения задач на деление и метод дополнения до двоек для решения задач на вычитание. Вы можете объединить это в один метод решения проблем разделения, используя следующие шаги. Если хотите, вы можете попытаться понять это самостоятельно, прежде чем продолжить.

Шаг 4. Вычтите делитель из делимого, добавив двоичное дополнение
Давайте рассмотрим задачу 100011 ÷ 000101. Первый шаг - решить 100011 - 000101, используя метод дополнения двоек, чтобы превратить ее в задачу сложения:
- Дополнение до двоек 000101 = 111010 + 1 = 111011
- 100011 + 111011 = 1011110
- Отбросить бит переноса → 011110

Шаг 5. Добавьте единицу к частному
В компьютерной программе это точка, в которой частное увеличивается на единицу. На бумаге сделайте пометку где-нибудь в углу, чтобы ее не перепутали с другими вашими работами. Мы успешно вычитали один раз, так что пока частное равно 1.

Шаг 6. Повторите, вычитая делитель из остатка
Результатом нашего последнего вычисления является остаток, оставшийся после того, как делитель «вошел» один раз. Продолжайте каждый раз добавлять двоичное дополнение делителя и отбрасывать бит переноса. Добавляйте единицу к частному каждый раз, повторяя, пока не получите остаток, равный или меньший, чем ваш делитель:
- 011110 + 111011 = 1011001 → 011001 (частное 1 + 1 = 10)
- 011001 + 111011 = 1010100 → 010100 (частное 10 + 1 = 11)
- 010100 + 111011 = 1001111 → 001111 (11+1=100)
- 001111 + 111011 = 1001010 → 001010 (100+1=101)
- 001010 + 111011 = 10000101 → 0000101 (101+1=110)
- 0000101 + 111011 = 1000000 → 000000 (110+1=111)
- 0 меньше 101, поэтому мы останавливаемся на этом. Частное 111 это ответ на проблему разделения. Остаток - это окончательный результат нашей задачи на вычитание, в данном случае 0 (без остатка).
Видео - с помощью этой службы некоторая информация может быть передана YouTube
подсказки
- Перед вычислением игнорируйте знаковую цифру в знаковых двоичных числах, кроме случаев определения положительного или отрицательного ответа.
- Метод вычитания с дополнением до двоек не сработает, если в ваших числах разное количество цифр. Чтобы исправить это, добавьте начальные нули к меньшему числу.
- Инструкции по увеличению, уменьшению или выталкиванию стека должны быть рассмотрены перед применением любых двоичных математических вычислений к набору машинных команд.
