Как рассчитать стандартное отклонение: 13 шагов (с изображениями)

Стандартное отклонение показывает, насколько разбросаны числа в выборке. Как только вы узнаете, какие числа и уравнения использовать, вычислить стандартное отклонение стало просто!

Шаги

Часть 1 из 3: В поисках среднего

Шаг 1. Посмотрите на свой набор данных

Это важный шаг в любом типе статистических расчетов, даже если это простая цифра, такая как среднее значение или медиана.

Знайте, сколько чисел в вашей выборке.
Различаются ли числа в большом диапазоне? Или разница между числами небольшая, например, всего несколько десятичных знаков?
Знайте, какие данные вы просматриваете. Что означают ваши числа в вашей выборке? это может быть что-то вроде результатов тестов, показаний пульса, роста, веса и т. д.
Например, набор тестов составляет 10, 8, 10, 8, 8 и 4.

Шаг 2. Соберите все свои данные

Вам понадобится каждое число в вашей выборке, чтобы вычислить среднее значение.

Среднее значение - это среднее значение всех ваших точек данных.
Это вычисляется путем сложения всех чисел в вашей выборке, а затем деления этой цифры на количество чисел в вашей выборке (n).
В выборке тестов (10, 8, 10, 8, 8, 4) в выборке 6 цифр. Следовательно, n = 6.

Шаг 3. Сложите числа в образце

Это первая часть вычисления математического среднего или среднего значения.

Например, используйте набор данных с оценками викторины: 10, 8, 10, 8, 8 и 4.
10 + 8 + 10 + 8 + 8 + 4 = 48. Это сумма всех чисел в наборе данных или выборке.
Сложите числа еще раз, чтобы проверить свой ответ.

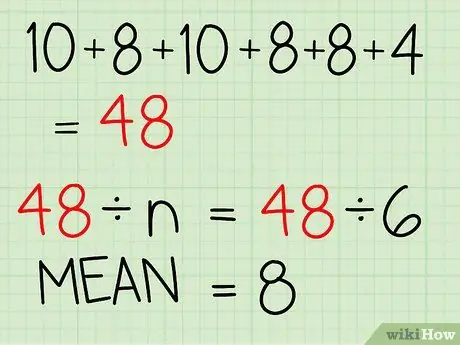
Шаг 4. Разделите сумму на количество чисел в вашей выборке (n)

Это даст среднее или среднее значение данных.

В выборке результатов тестов (10, 8, 10, 8, 8 и 4) шесть цифр, поэтому n = 6.
Сумма результатов тестов в этом примере составила 48. Итак, вы разделите 48 на n, чтобы вычислить среднее значение.
48 / 6 = 8
Средний тестовый балл по выборке - 8.

Часть 2 из 3: Поиск отклонений в вашей выборке

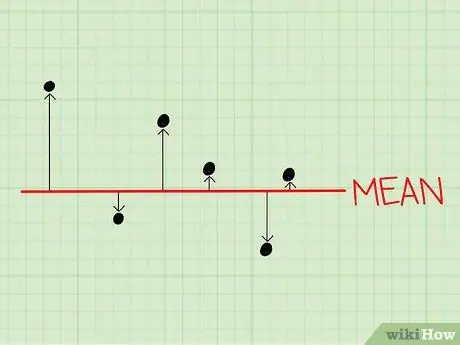
Шаг 1. Найдите дисперсию

Дисперсия - это показатель, который показывает, насколько данные в вашей выборке сгруппированы вокруг среднего значения.

Этот рисунок даст вам представление о том, насколько далеко разбросаны ваши данные.
В выборках с низкой дисперсией данные сгруппированы по среднему значению.
В выборках с высокой дисперсией данные сгруппированы далеко от среднего.
Дисперсия часто используется для сравнения распределения двух наборов данных.

Шаг 2. Вычтите среднее значение из каждого числа в вашей выборке

Это даст вам представление о том, насколько каждая точка данных отличается от среднего значения.

Например, в нашей выборке тестов (10, 8, 10, 8, 8 и 4) среднее или математическое среднее было 8.
10-8 = 2; 8-8 = 0, 10-8 = 2, 8-8 = 0, 8-8 = 0 и 4-8 = -4.
Повторите эту процедуру еще раз, чтобы проверить каждый ответ. Очень важно, чтобы каждая из этих цифр была правильной, поскольку они понадобятся вам на следующем этапе.

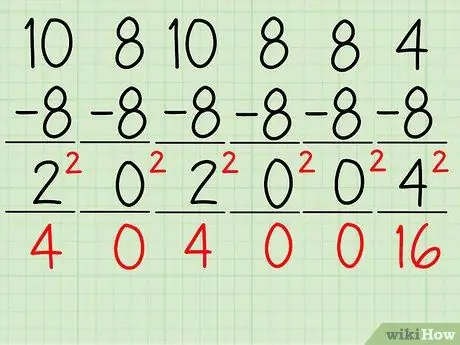
Шаг 3. Возведите в квадрат все числа из каждого вычитания, которое вы только что сделали

Вам понадобится каждая из этих цифр, чтобы узнать дисперсию в вашей выборке.

Помните, что в нашей выборке мы вычли среднее значение (8) из каждого числа в выборке (10, 8, 10, 8, 8 и 4) и получили следующее: 2, 0, 2, 0, 0 и -4.
Чтобы выполнить следующий расчет при определении дисперсии, вы должны выполнить следующее: 2², 0², 2², 0², 0², и (-4)² = 4, 0, 4, 0, 0 и 16.
Проверьте свои ответы, прежде чем переходить к следующему шагу.

Шаг 4. Сложите квадраты чисел

Эта цифра называется суммой квадратов.

В нашем примере результатов теста квадраты были следующими: 4, 0, 4, 0, 0 и 16.
Помните, что в примере с результатами тестов мы начали с вычитания среднего из каждой из оценок и возведения в квадрат этих цифр: (10-8) ^ 2 + (8-8) ^ 2 + (10-8) ^ 2 + (8 -8) ^ 2 + (8-8) ^ 2 + (4-8) ^ 2
4 + 0 + 4 + 0 + 0 + 16 = 24.
Сумма квадратов 24.

Шаг 5. Разделите сумму квадратов на (n-1)

Помните, что n - это количество чисел в вашем образце. Выполнение этого шага обеспечит дисперсию. Причина использования n-1 состоит в том, чтобы иметь несмещенную дисперсию выборки и дисперсию генеральной совокупности.

В нашей выборке тестов (10, 8, 10, 8, 8 и 4) 6 цифр. Следовательно, n = 6.
п-1 = 5.
Помните, что сумма квадратов для этого образца была 24.
24 / 5 = 4.8
Таким образом, дисперсия в этой выборке составляет 4,8.

Часть 3 из 3: Расчет стандартного отклонения

Шаг 1. Найдите свой показатель дисперсии

Это понадобится вам, чтобы найти стандартное отклонение для вашего образца.

Помните, что дисперсия - это степень отклонения ваших данных от среднего или математического среднего.
Стандартное отклонение - это аналогичный показатель, который показывает, насколько разбросаны ваши данные в вашей выборке.
В нашем примере выборки результатов тестов дисперсия составила 4,8.

Шаг 2. Извлеките квадратный корень из дисперсии

Это стандартное отклонение.

Обычно по крайней мере 68% всех образцов попадают в одно стандартное отклонение от среднего.
Помните, что в нашей выборке результатов тестов дисперсия составила 4,8.
√4,8 = 2,19. Таким образом, стандартное отклонение в нашей выборке результатов тестов составляет 2,19.
5 из 6 (83%) из нашей выборки результатов тестов (10, 8, 10, 8, 8 и 4) находятся в пределах одного стандартного отклонения (2,19) от среднего значения (8).

Шаг 3. Снова найдите среднее значение, дисперсию и стандартное отклонение

Это позволит вам проверить свой ответ.

При выполнении расчетов вручную или с помощью калькулятора важно записывать все этапы решения проблемы.
Если во второй раз вы получите другую цифру, проверьте свою работу.
Если вы не можете найти, где допустили ошибку, начните с третьего раза, чтобы сравнить свою работу.