Расчет совокупной частоты дает вам сумму (или промежуточный итог) всех частот до определенной точки в наборе данных. Этот показатель отличается от абсолютной частоты, которая относится к тому, сколько раз конкретное значение появляется в наборе данных. Кумулятивная частота особенно полезна при попытке ответить на вопрос «больше чем» или «меньше чем» о генеральной совокупности или для проверки правильности некоторых ваших расчетов. Упорядочив значения и сложив их, вы можете быстро вычислить совокупную частоту для любого набора данных, который у вас есть.
Шаги
Часть 1 из 2: Базовая совокупная частота
Шаг 1. Отсортируйте набор данных
«Набор данных» - это просто группа чисел, которую вы изучаете. Отсортируйте эти значения в порядке от наименьшего к наибольшему.
Пример. В вашем наборе данных указано количество книг, прочитанных каждым учащимся за последний месяц. После сортировки это набор данных: 3, 3, 5, 6, 6, 6, 8

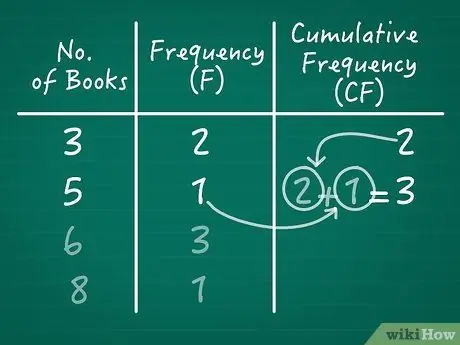
Шаг 2. Подсчитайте абсолютную частоту каждого значения
Частота значения - это количество раз, которое оно появляется. (Вы можете назвать это «абсолютной частотой», когда вам нужно избежать путаницы с совокупной частотой.) Самый простой способ отслеживать это - начать график. Напишите «Значение» (или описание того, что измеряет значение) в начале первого столбца. Напишите «Частота» вверху второго столбца. Заполните таблицу для каждого значения.
- Пример: напишите «Количество книг» вверху первого столбца. Напишите «Частота» вверху второго столбца.
- Во второй строке запишите первое значение в поле Количество книг: 3.
- Подсчитайте количество троек в вашем наборе данных. Так как есть две тройки, напишите 2 под «Частотой» в той же строке.
-
Повторите для каждого значения, пока не получите полную диаграмму:
- 3 | F = 2
- 5 | F = 1
- 6 | F = 3
- 8 | F = 1

Шаг 3. Найдите совокупную частоту первого значения
Совокупная частота отвечает на вопрос «сколько раз появляется это значение или меньшее значение?» Всегда начинайте с наименьшего значения в вашем наборе данных. Поскольку нет меньших значений, ответ будет таким же, как и абсолютная частота этого значения.
-
Пример: Наше наименьшее значение - 3. Количество студентов, прочитавших 3 книги, равно 2. Никто не прочитал меньше этого числа, поэтому совокупная частота равна 2. Добавьте это в первую строку вашей диаграммы:
3 | F = 2 | CF = 2
Шаг 4. Найдите совокупную частоту следующего значения
Переходите к следующему значению на вашей диаграмме. Мы только что выяснили, сколько раз появлялись более низкие значения. Чтобы найти кумулятивную частоту этого значения, нам просто нужно добавить его абсолютную частоту к промежуточной сумме. Другими словами, возьмите последнюю найденную кумулятивную частоту, а затем добавьте абсолютную частоту этого значения.
-
Пример:
-
3 | F = 2 | CF =
Шаг 2.
-
5 | F =
Шаг 1. | CF
Шаг 2.
Шаг 1. = 3
-

Шаг 5. Повторите для остальных значений
Продолжайте двигаться к все большим и большим значениям. Каждый раз добавляйте последнюю накопленную частоту к абсолютной частоте следующего значения.
-
Пример:
-
3 | F = 2 | CF =
Шаг 2.
-
5 | F = 1 | CF = 2 + 1 =
Шаг 3.
-
6 | F = 3 | CF = 3 + 3 =
Шаг 6.
-
8 | F = 1 | CF = 6 + 1 =
Шаг 7.
-

Шаг 6. Проверьте свою работу
Когда вы закончите, вы сложите количество появлений каждой переменной. Окончательная совокупная частота должна равняться общему количеству точек данных в вашем наборе. Проверить это можно двумя способами:
- Сложите все отдельные частоты вместе: 2 + 1 + 3 + 1 = 7, и это наша окончательная совокупная частота.
- Подсчитайте количество точек данных. В нашем списке было 3, 3, 5, 6, 6, 6, 8. Всего 7 пунктов, это наша окончательная совокупная частота.
Часть 2 из 2: расширенное использование

Шаг 1. Разберитесь в дискретных и непрерывных данных
Дискретные данные поступают в единицах, которые вы можете сосчитать, когда невозможно найти часть единицы. Непрерывные данные описывают что-то неисчислимое, с измерениями, которые могут находиться где угодно между любыми выбранными вами единицами. Вот пара примеров:
- Количество собак: Дискретное. Нет такой вещи, как половина собаки.
- Глубина снежного покрова: Сплошная. Снег накапливается постепенно, а не по частям. Если вы попытаетесь измерить его в дюймах, вы можете найти сугробы глубиной 5,6 дюйма.

Шаг 2. Сгруппируйте непрерывные данные по диапазону
Непрерывные наборы данных часто содержат большое количество уникальных переменных. Если вы попытаетесь использовать описанный выше метод, ваша диаграмма будет очень длинной и трудной для понимания. Вместо этого сделайте каждую строку диаграммы диапазоном значений. Важно, чтобы каждый диапазон был одинакового размера (например, 0-10, 11-20, 21-30 и т. Д.), Независимо от того, сколько значений находится в каждом диапазоне. Вот пример непрерывного набора данных, преобразованного в диаграмму:
- Набор данных: 233, 259, 277, 278, 289, 301, 303
-
Диаграмма (значение первого столбца, частота второго столбца, совокупная частота третьего столбца):
- 200-250 | 1 | 1
- 251-300 | 4 | 1 + 4 = 5
- 301-350 | 2 | 5 + 2 = 7
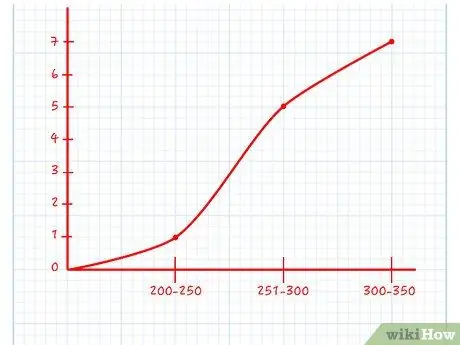
Шаг 3. Постройте линейный график
После того, как вы рассчитали совокупную частоту, возьмите миллиметровую бумагу. Нарисуйте линейный график с осью X, равной значениям вашего набора данных, и осью Y, равной совокупной частоте. Это значительно упростит следующие расчеты.
- Например, если ваш набор данных идет от 1 до 8, нарисуйте ось x с отмеченными на ней восемью единицами. На каждом значении на оси x нарисуйте точку на значении y, которое равно накопленной частоте для этого значения. Соедините каждую пару соседних точек линией.
- Если для определенного значения нет точек данных, абсолютная частота равна 0. Добавление 0 к последней совокупной частоте не меняет ее значения, поэтому нарисуйте точку с тем же значением y, что и последнее значение.
- Поскольку совокупная частота всегда увеличивается вместе со значениями, ваш линейный график всегда должен оставаться устойчивым или повышаться при движении вправо. Если линия в какой-то момент опускается, возможно, вы по ошибке смотрите на абсолютную частоту.
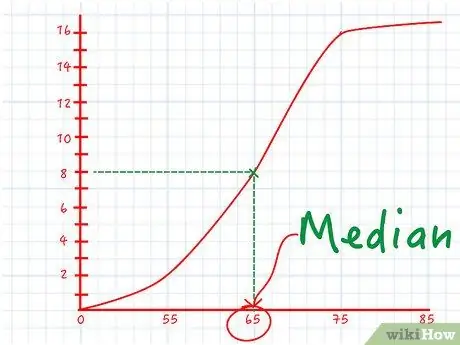
Шаг 4. Найдите медиану на линейном графике
Медиана - это значение точно посередине набора данных. Половина значений выше медианы, а половина - ниже. Вот как найти медиану на линейном графике:
- Посмотрите на последнюю точку в дальнем правом углу вашего графика. Его значение y - это общая накопленная частота, которая представляет собой количество точек в наборе данных. Допустим, это значение 16
- Умножьте это значение на ½ и найдите его по оси ординат. В нашем примере половина 16 равна 8. Найдите 8 на оси ординат.
- Найдите точку на линейном графике при этом значении y. Переместите палец от восьмерки на оси Y через график. Остановитесь, когда ваш палец коснется линии вашего графика. Это точка, в которой была подсчитана ровно половина ваших точек данных.
- Найдите ось абсцисс в этой точке. Проведите пальцем прямо вниз, чтобы увидеть значение оси X. Это значение является медианой вашего набора данных. Например, если это значение 65, то половина вашего набора данных ниже 65, а половина - выше 65.
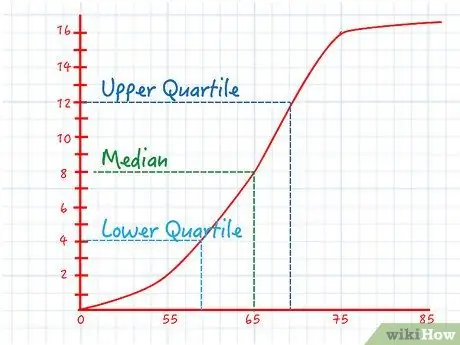
Шаг 5. Найдите квартили на линейном графике
Квартили делят данные на четыре части. Этот процесс очень похож на поиск медианы. Единственная разница в том, как найти значения y:
- Чтобы найти значение оси Y нижнего квартиля, возьмите максимальную совокупную частоту и умножьте на. Соответствующее значение x сообщает вам значение с ровно ¼ данных под ним.
- Чтобы найти значение оси Y верхнего квартиля, умножьте максимальную совокупную частоту на ¾. Соответствующее значение x сообщает вам значение с ровно данных под ним и ¼ над ним.