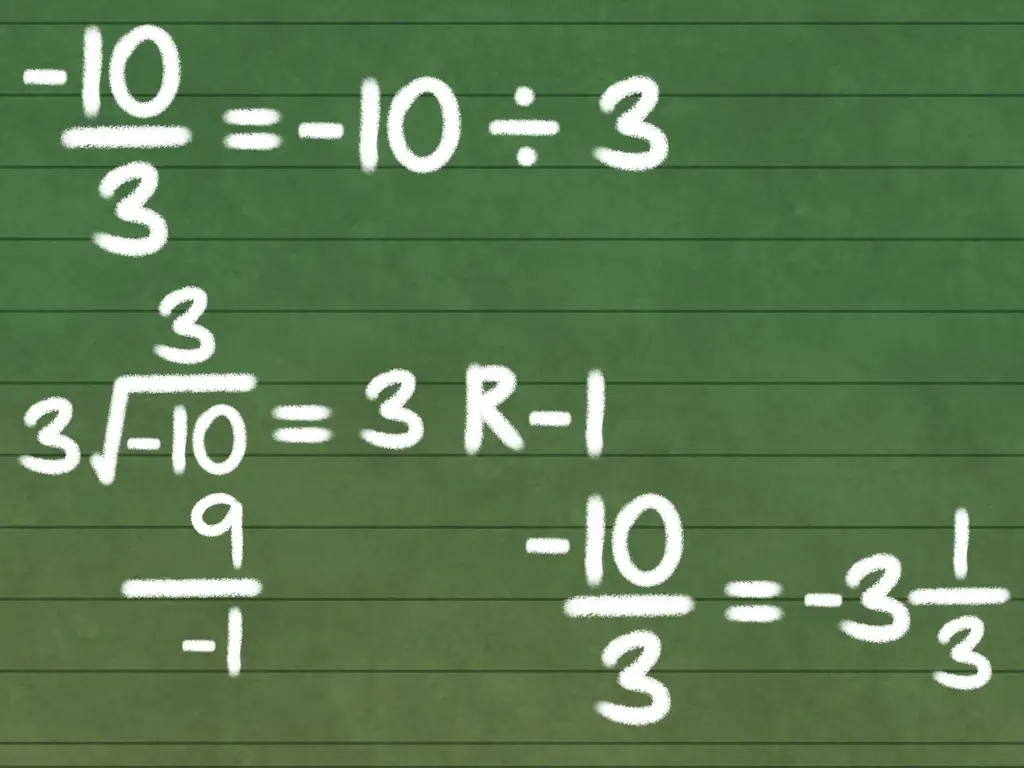В математике неправильные дроби - это дроби, в которых числитель (верхняя половина) - это число, которое больше или равно знаменателю (нижняя половина). Чтобы преобразовать неправильную дробь в смешанное число (состоящее из дроби и целого числа, например 2 и 3/4), разделите числитель на знаменатель.
Напишите ответ целого числа рядом с дробью с остатком в числителе и исходном знаменателе - теперь у вас есть смешанная дробь!
Шаги
Метод 1 из 2: преобразование неправильной дроби
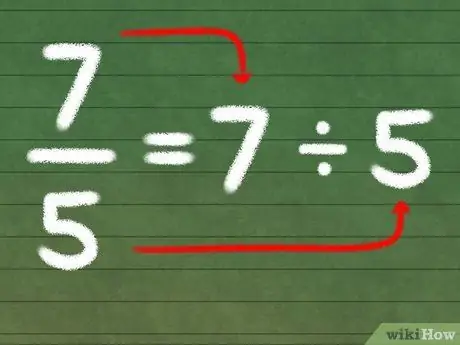
Шаг 1. Разделите числитель на знаменатель
Начните с написания неправильной дроби. Затем разделите числитель на знаменатель - другими словами, просто решите задачу деления, для которой дробь уже настроена. Не забудьте указать остаток.
- Давайте рассмотрим пример. Допустим, нам нужно превратить дробь 7/5 в смешанное число. Начнем с деления 7 на 5, вот так:
- 7/5 → 7 ÷ 5 = 1 R2
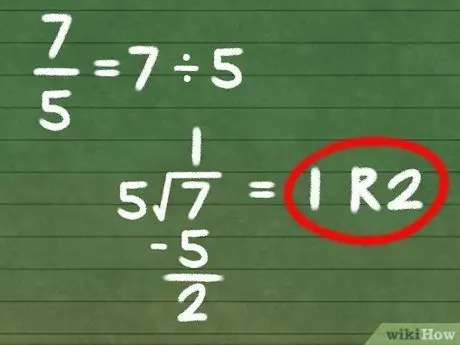
Шаг 2. Напишите ответ целиком
Целочисленная часть вашего смешанного числа (большое число слева от дроби) - это целочисленный ответ на вашу задачу деления. Другими словами, просто напишите ответ на задачу деления без остатка.
-
В нашем примере, поскольку наш ответ - 1 R2, мы оставим остаток и просто напишем 1.
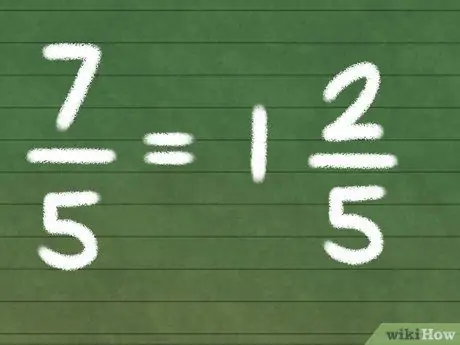
Шаг 3. Сделайте дробь из остатка и первоначального знаменателя
Теперь нам нужно найти дробную часть смешанного числа. Поместите остаток от задачи деления в числитель и используйте тот же знаменатель, что и исходная неправильная дробь. Поместите эту дробь рядом со своим целым числом, и вы получите смешанное число!
- В нашем примере остаток равен 2. Подставив это значение над нашим первоначальным знаменателем (5), мы получим 2/5. Мы помещаем это рядом с нашим целым числом answer (1), чтобы получить окончательное смешанное число, например:
- 1 2/5.
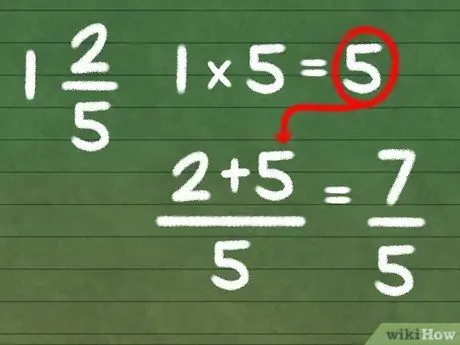
Шаг 4. Чтобы вернуться к неправильной дроби, добавьте целое число в числитель
Смешанные числа хорошо смотрятся на бумаге и легко читаются, но это не всегда лучший выбор. Например, если мы умножаем дробь и смешанное число, наша работа будет намного проще, если мы обратим смешанное число в неправильную дробь. Для этого просто умножьте целое число на знаменатель и прибавьте его к числителю.
- Если бы мы хотели преобразовать наш пример ответа (1 2/5) обратно в неправильную дробь, мы бы сделали это следующим образом:
- 1 × 5 = 5 → (2 + 5)/5 = 7/5
Метод 2 из 2: решение типовых проблем
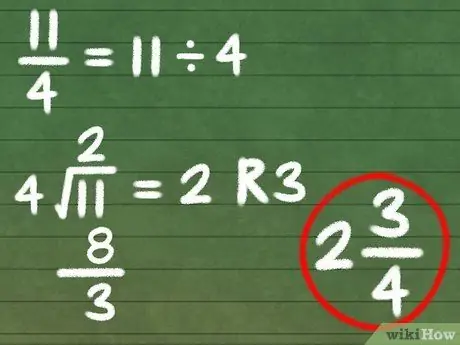
Шаг 1. Преобразуйте 11/4 в смешанное число
Это простая задача - решите точно так же, как указано выше. См. Пошаговое решение ниже.
- 11/4 - для начала нам нужно числитель разделить на знаменатель.
- 11 ÷ 4 = 2 R 3 - теперь нам нужно составить дробь из остатка и нашего первоначального знаменателя.
- 11/4 = 2 3/4
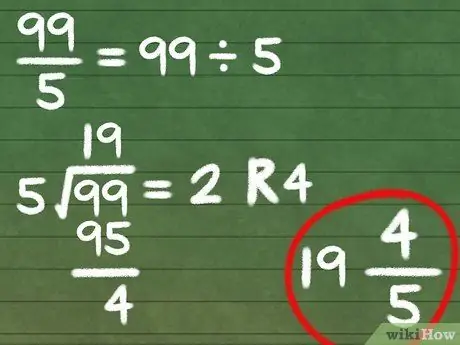
Шаг 2. Преобразуйте 99/5 в смешанное число
Здесь мы имеем дело с действительно большим числителем, но не пугайтесь - процесс точно такой же! См. ниже:
- 99/5 - сколько раз 5 входит в 99? Поскольку 5 переходит в 100 ровно 20 раз, можно с уверенностью сказать, что 5 переходит в 99 19 раз.
- 99 ÷ 5 = 19 R 4 - теперь мы просто сложили смешанные числа вместе, как и раньше.
- 99/5 = 19 4/5

Шаг 3. Преобразуйте 6/6 в смешанное число
До сих пор мы имели дело только с неправильными дробями, у которых числитель больше знаменателя. Но что происходит, когда они совпадают? См. Ниже, чтобы узнать.
- 6/6 - шесть переходит в шесть один раз без остатка, очевидно.
- 6 ÷ 6 = 1 R0. Поскольку дробь с 0 в числителе всегда равна нулю, нам не нужно ставить дробь рядом с нашим целым числом.
-
6/6 =
Шаг 1.
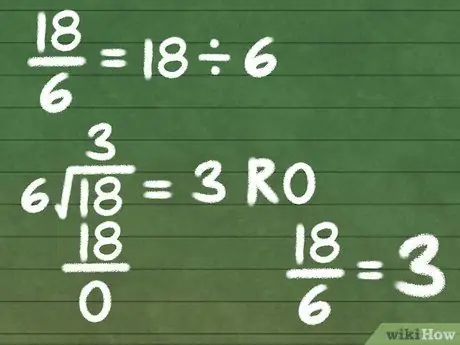
Шаг 4. Преобразуйте 18/6 в смешанное число
Если числитель кратен знаменателю, вам не нужно беспокоиться об остатке - просто решите задачу деления, чтобы получить ответ. См. ниже.
- 18/6 - поскольку мы знаем, что 18 - это всего лишь 6 × 3, мы знаем, что у нас будет остаток 0, поэтому нам не нужно беспокоиться о дробной части нашего смешанного числа.
-
18/6 =
Шаг 3.
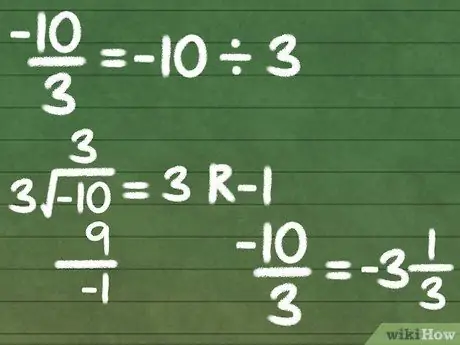
Шаг 5. Преобразуйте -10/3 в смешанное число
Отрицательные числа работают точно так же, как положительные числа. См. ниже:
- -10/3
- -10 ÷ 3 = -3 R1
- -10/3 = - 3 1/3
подсказки
- Неправильные дроби не обязательно плохо. На самом деле, иногда они более полезны, чем смешанные числа. Например, если вы собираетесь умножить две дроби, неправильные дроби лучше, потому что вам просто нужно умножить числитель и знаменатель, чтобы получить ответ: например, 1/6 × 7/2 = 7/12. Теперь попробуйте умножить 1/6 × 3 1/2 - не все так просто.
- С другой стороны, смешанные числа обычно лучше всего подходят для описания чего-либо в реальной жизни. Например, если рецепт требует 4 1/2 стакана муки, вы не скажете: «Нам нужно 9/2 стакана муки».