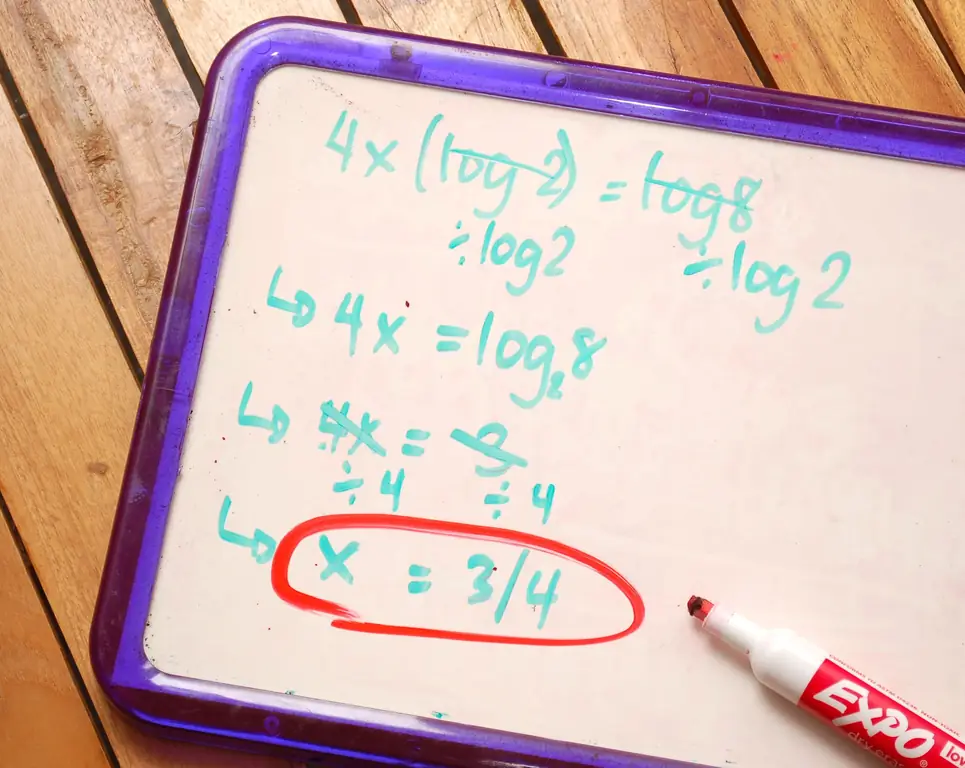Смущает логарифм? Не волнуйтесь! Логарифм (сокращенно log) - это просто показатель степени в другой форме. Что касается логарифмов, важно понимать, почему мы их используем, а именно для решения уравнений, в которых наша переменная находится в экспоненте, и мы не можем получить аналогичные основания.
бревноаx = y совпадает с aу = х.
Шаги
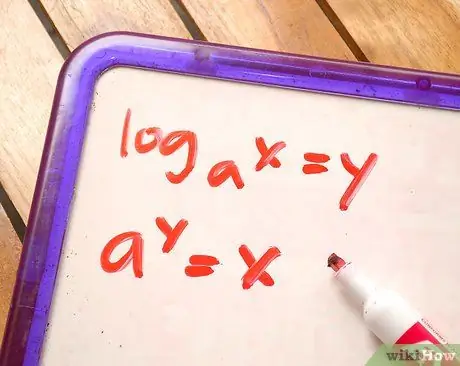
Шаг 1. Узнайте разницу между логарифмическими и экспоненциальными уравнениями
Это очень простой первый шаг. Если он содержит логарифм (например: журналах = у) это логарифмическая проблема. Логарифм обозначается буквами "бревно". Если уравнение содержит экспоненту (то есть переменную в степени), это экспоненциальное уравнение. Показатель степени - это верхний индекс, помещаемый после числа.
- Логарифмический: журналах = у
- Экспонента: aу = х
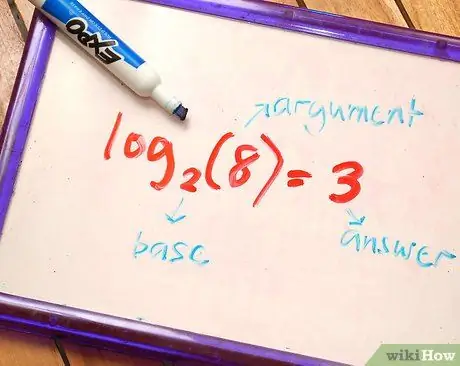
Шаг 2. Знать части логарифма
Основание - это номер нижнего индекса, который находится после букв «журнал» - 2 в этом примере. Аргумент или число - это число после нижнего индекса - 8 в этом примере. Наконец, ответ - это число, которое логарифмическое выражение установлено равным - 3 в этом уравнении.
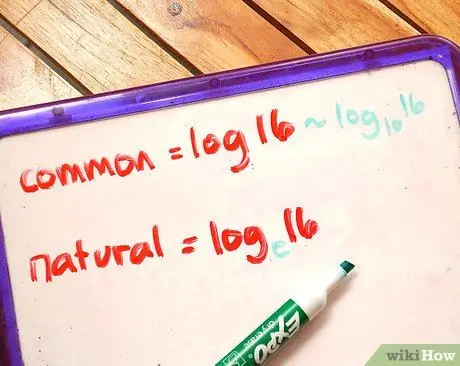
Шаг 3. Узнайте разницу между обычным журналом и натуральным журналом
- Общие журналы иметь базу 10. (например, log10Икс). Если журнал записывается без основания (как log x), предполагается, что он имеет основание 10.
- Натуральные бревна: Это журналы с основанием e. e - математическая константа, равная пределу (1 + 1 / n) когда n приближается к бесконечности, что приблизительно равно 2,718281828. Чем больше значение, которое мы подставляем для n, тем ближе мы приближаемся к 2,71828. Важно понимать, что 2,71828 или e не является точным значением. Вы можете думать об этом как о значении числа пи, в котором после десятичной точки стоит бесконечное количество цифр. Другими словами, это иррациональное число, которое мы округляем до 2,71828. Также журналеx часто записывается как ln x. Например, ln 20 означает натуральный логарифм 20, и поскольку основание натурального логарифма равно e, или 2,71828, значение натурального логарифма 20 приблизительно равно 3, потому что 2,71828 до 3-го примерно равно 20. Примечание. чем вы можете найти натуральный логарифм 20 на вашем калькуляторе, используя кнопку LN. Натуральные журналы имеют решающее значение для углубленного изучения математики и естественных наук, и вы узнаете больше об их использовании в будущих курсах. Однако пока важно познакомиться с основами натурального логарифма.
- Другие журналы: Другие журналы имеют основание, отличное от общего журнала и математической базовой константы E. Двоичные журналы имеют основание 2 (например, журнал2Икс). Шестнадцатеричные журналы имеют основу из 16. Журналы с 64th base используются в области Advanced Computer Geometry (ACG).
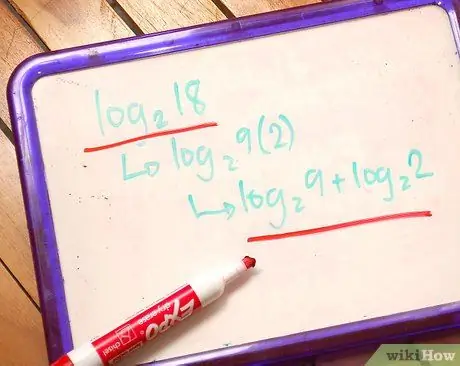
Шаг 4. Знать и применять свойства логарифмов
Свойства логарифмов позволяют решать логарифмические и экспоненциальные уравнения, которые иначе были бы невозможны. Они работают, только если основание a и аргумент положительны. Также основание a не может быть 1 или 0. Свойства логарифмов перечислены ниже с отдельным примером для каждого логарифма с числами вместо переменных. Эти свойства используются при решении уравнений.
-
бревноа(xy) = журналаx + журналау
Журнал из двух чисел, x и y, которые умножаются друг на друга, можно разделить на два отдельных журнала: журнал каждого из суммируемых факторов. (Это также работает в обратном направлении.)
Пример:
бревно216 =
бревно28*2 =
бревно28 + журнал22
-
бревноа(x / y) = журналаx - журналау
Журнал из двух чисел, разделенных друг на друга, x и y, может быть разделен на два журнала: журнал делимого x минус журнал делителя y.
Пример:
бревно2(5/3) =
бревно25 - журнал23
-
бревноа(Икср) = r * журналаИкс
Если аргумент x журнала имеет показатель степени r, показатель степени можно переместить в начало логарифма.
Пример:
бревно2(65)
5 * журнал26
-
бревноа(1 / x) = -logаИкс
Подумайте об аргументе. (1 / x) равно x-1. По сути, это еще одна версия предыдущего свойства.
Пример:
бревно2(1/3) = -log23
-
бревноаа = 1
Если основание a равно аргументу a, ответ будет 1. Это очень легко запомнить, если думать о логарифме в экспоненциальной форме. Сколько раз нужно умножить a на себя, чтобы получить a? Один раз.
Пример:
бревно22 = 1
-
бревноа1 = 0
Если аргумент один, ответ всегда равен нулю. Это свойство выполняется, потому что любое число с нулевым показателем равно единице.
Пример:
бревно31 =0
-
(бревнобх / журналба) = журналаИкс
Это называется «смена базы». Одно бревно, разделенное на другое, оба с одинаковым основанием b, равно одному бревну. Аргумент знаменателя a становится новым основанием, а аргумент x числителя становится новым аргументом. Это легко запомнить, если вы подумаете о основании как о нижней части объекта, а знаменатель - как о нижней части дроби.
Пример:
бревно25 = (журнал 5 / журнал 2)

Шаг 5. Попрактикуйтесь в использовании свойств
Эти свойства лучше всего запоминать при многократном использовании при решении уравнений. Вот пример уравнения, которое лучше всего решить с одним из свойств:
4x * log2 = log8 Разделите обе стороны на log2.
4x = (log8 / log2) Использовать изменение базы.
4x = журнал28 Вычислите значение журнала.
4x = 3 Разделите обе стороны на 4. x = 3/4 Решено. Это очень полезно. Теперь я разбираюсь в логах.