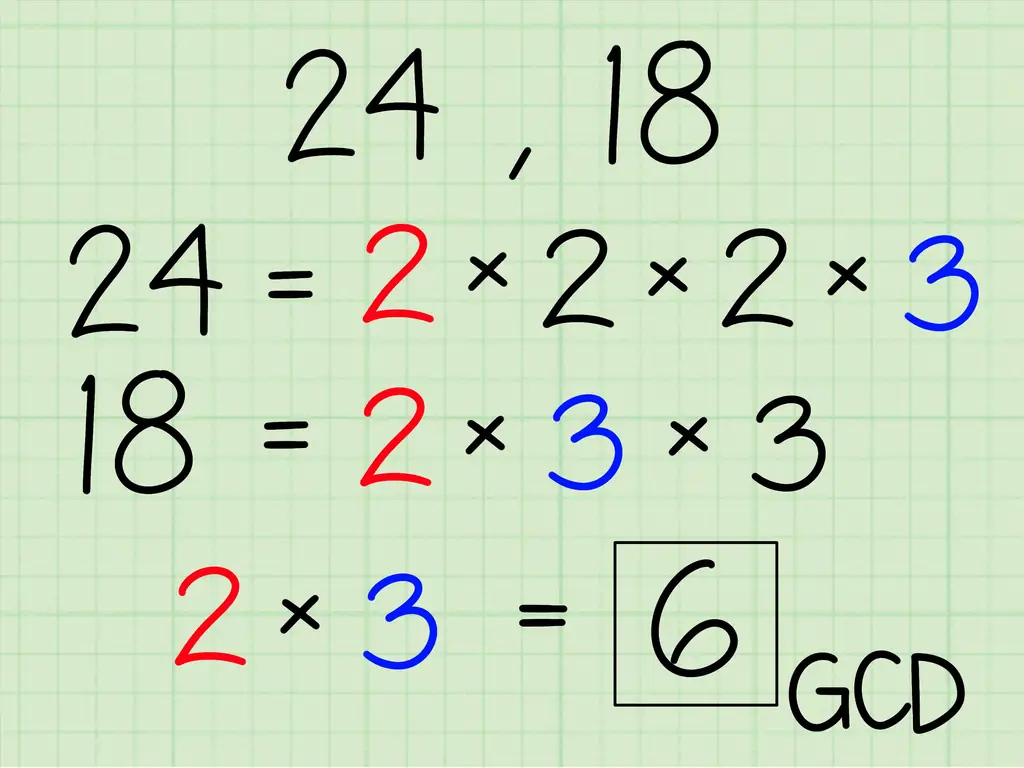Наибольший общий делитель (GCD) двух целых чисел, также называемый наибольшим общим множителем (GCF) и наибольшим общим множителем (HCF), является наибольшим целым числом, которое является делителем (множителем) обоих из них. Например, наибольшее число, которое делится как на 20, так и на 16, равно 4. (И 16, и 20 имеют более крупные множители, но не более крупные общие множители - например, 8 - это множитель 16, но не множитель 20.) В начальной школе большинство людей обучается методу поиска НОД методом «угадывай и проверяй». Вместо этого есть простой и систематический способ сделать это, который всегда приводит к правильному ответу. Метод получил название «алгоритм Евклида». Если вы хотите узнать, как найти наибольший общий делитель двух целых чисел, см. Шаг 1, чтобы начать работу.
Шаги
Метод 1 из 2: использование алгоритма делителя

Шаг 1. Отбросьте все отрицательные знаки
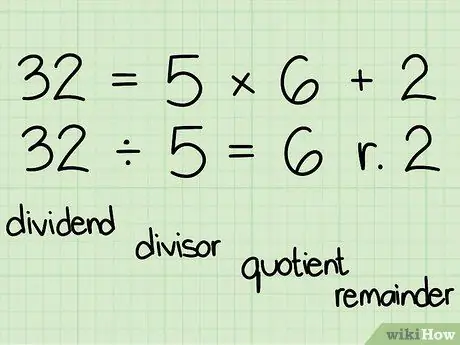
Шаг 2. Знайте свой словарный запас:
когда вы делите 32 на 5,
-
- 32 - дивиденд
- 5 - делитель
- 6 - частное
- 2 - это остаток (или по модулю).

Шаг 3. Найдите большее из двух чисел
Это будет дивиденд, и тем меньше делитель.

Шаг 4. Запишите этот алгоритм:
(делимое) = (делитель) * (частное) + (остаток)

Шаг 5. Поместите большее число в поле делимого, а меньшее число в качестве делителя

Шаг 6. Решите, во сколько раз меньшее число разделится на большее число, и введите его в алгоритм как частное

Шаг 7. Вычислите остаток и подставьте его в соответствующее место в алгоритме

Шаг 8. Запишите алгоритм еще раз, но на этот раз A) используйте старый делитель в качестве нового делимого и B) используйте остаток в качестве нового делителя

Шаг 9. Повторяйте предыдущий шаг, пока остаток не станет равен нулю

Шаг 10. Последний делитель - наибольший общий делитель

Шаг 11. Вот пример, в котором мы пытаемся найти НОД 108 и 30:

Шаг 12. Обратите внимание на то, как 30 и 18 в первой строке меняют положение, создавая вторую линию
Затем 18 и 12 сдвигаются, чтобы создать третью линию, а 12 и 6 сдвигаются, чтобы создать четвертую линию. Цифры 3, 1, 1 и 2, следующие за символом умножения, больше не появляются. Они представляют, сколько раз делитель входит в делимое, поэтому они уникальны для каждой строки.
Метод 2 из 2: Использование основных факторов
Шаг 1. Отбросьте все отрицательные знаки
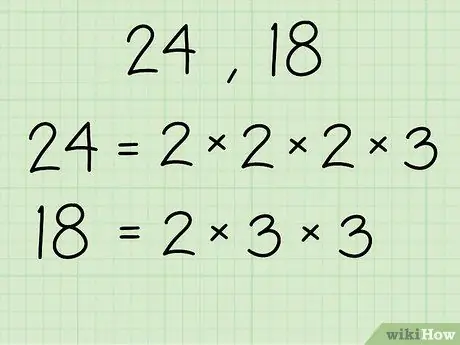
Шаг 2. Найдите факторизацию чисел на простые множители и перечислите их, как показано
-
Используя числа 24 и 18 в качестве примеров:
- 24-2 х 2 х 2 х 3
- 18-2 х 3 х 3
-
Используя числа 50 и 35 в качестве примеров:
- 50-2 х 5 х 5
- 35-5 х 7
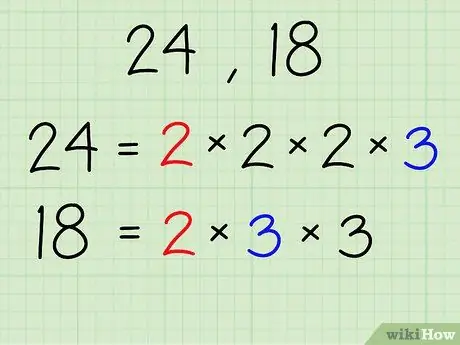
Шаг 3. Определите все общие простые множители
-
Используя числа 24 и 18 в качестве примеров:
-
24-
Шаг 2. х 2 х 2
Шаг 3.
-
18-
Шаг 2.
Шаг 3. х 3
-
-
Используя числа 50 и 35 в качестве примеров:
-
50-2 х
Шаг 5. х 5
-
35-
Шаг 5. х 7
-
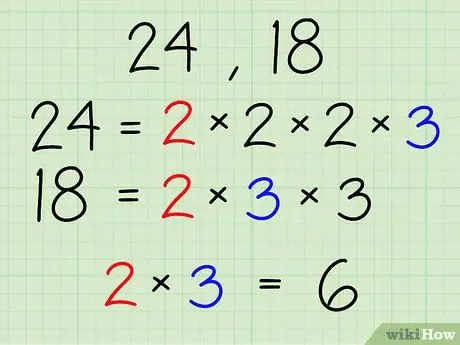
Шаг 4. Умножьте общие множители
-
В случае 24 и 18 умножьте
Шаг 2. ан
Шаг 3. вместе, чтобы ge
Шаг 6.. Шесть - это наибольший общий делитель 24 и 18.
-
В случае 50 и 35 умножать нечего.
Шаг 5. является единственным общим фактором и, следовательно, самым большим.
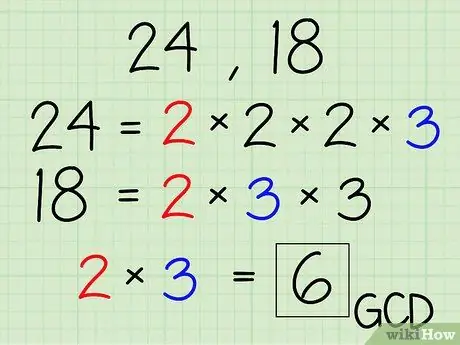
Шаг 5. Готово
подсказки
- Один из способов записать это, используя обозначение mod = остаток, состоит в том, что GCD (a, b) = b, если a mod b = 0, и GCD (a, b) = GCD (b, a mod b) в противном случае.
- В качестве примера найдем НОД (-77, 91). Во-первых, используйте 77 вместо -77, чтобы GCD (-77, 91) превратился в GCD (77, 91). Теперь 77 меньше 91, поэтому мы должны поменять их местами, но давайте посмотрим, как алгоритм позаботится об этом, если мы этого не сделаем. Когда мы вычисляем 77 mod 91, мы получаем 77 (так как 77 = 91 x 0 + 77). Поскольку это не ноль, мы меняем (a, b) на (b, a mod b) и получаем: GCD (77, 91) = GCD (91, 77). 91 mod 77 дает 14 (помните, это означает, что 14 - это остаток). Поскольку это не ноль, замените GCD (91, 77) на GCD (77, 14). 77 mod 14 дает 7, которое не равно нулю, поэтому замените GCD (77, 14) на GCD (14, 7). 14 mod 7 равно нулю, так как 14 = 7 * 2 без остатка, поэтому мы останавливаемся. А это значит: НОД (-77, 91) = 7.
- Этот прием очень полезен при уменьшении дробей. В приведенном выше примере дробь -77/91 уменьшается до -11/13, потому что 7 является наибольшим общим делителем -77 и 91.
- Если 'a' и 'b' оба равны нулю, то любое ненулевое число делит их оба, поэтому технически в этом случае нет наибольшего общего делителя. Математики часто просто говорят, что наибольший общий делитель 0 и 0 равен 0, и это ответ, который дает этот метод.