Теория групп - это раздел абстрактной алгебры, который имеет дело с алгебраическими структурами, называемыми группами. Группы встречаются в математике и повлияли на многие разделы алгебры. В этой статье рассказывается, как изучать теорию групп.
Шаги

Шаг 1. Разберитесь в теории множеств
Множества - это четко определенные наборы объектов. Теория множеств важна для изучения теории групп. Узнайте о множествах, операциях над ними и декартовом произведении множеств.
- Используйте формальные определения множеств, потому что вам нужна такая строгость для полного понимания теории множеств.
- Изучите аксиомы теории множеств Цермело - Френкеля.
- Хотя базовых понятий множеств было бы достаточно, чтобы начать с теории групп, всегда намного лучше узнать немного больше, чем требуется!

Шаг 2. Узнайте о наборе действительных чисел, его подмножествах, таких как рациональные числа, и его свойствах
Натуральные числа, целые числа, рациональные и иррациональные числа и целые числа - все это подмножества действительных чисел, и, хотя у них есть некоторые общие свойства, существуют различные свойства каждого подмножества.
- Узнайте о свойствах действительных чисел. Например, квадрат действительного числа всегда неотрицателен.
- Узнайте об отличительных свойствах некоторых подмножеств действительных чисел. Например, квадрат рационального числа всегда рационально, но квадрат иррационального числа может быть рациональным или иррациональным.
- Используйте эти свойства и активно ссылайтесь на них всякий раз, когда вы что-то решаете или доказываете. Например, если у вас есть проблема, в которой используется какое-то ненулевое действительное число «а». Если вы делите с помощью «a», укажите, что это разрешено, поскольку a задано как ненулевое.

Шаг 3. Изучите реальные функции
Изучите определения функций, домена, субдомена и диапазона функции. Также изучите типы функций, такие как инъекции и сюръекции, а также существование обратной функции.
- Изучите графики. Графики дают обширное представление о поведении функции. Например, квадратичная функция f (x) = ax ^ 2 + bx + c либо касается оси x один раз, что означает, что существует повторяющийся корень уравнения f (x) = 0, либо обрезает его дважды, что подразумевает f (x) = 0 имеет два различных действительных корня или вообще не пересекает ось x, что означает, что не существует реальных решений для f (x) = 0.
- Изучите некоторые специальные функции, такие как тригонометрические функции и факториальные, экспоненциальные, знаковые функции, их свойства и графики.
- Также узнайте об отношениях и их свойствах.
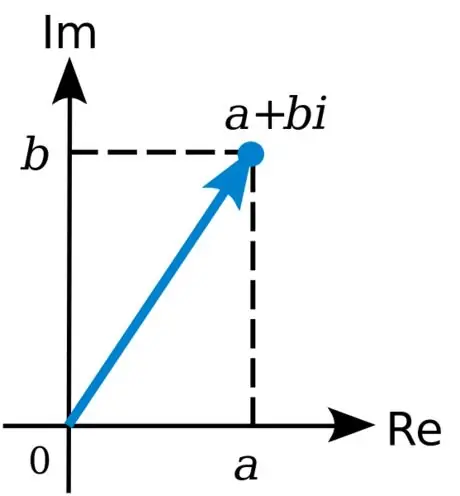
Шаг 4. Ознакомьтесь с комплексными числами
Узнайте об их форме, свойствах, модуле и сопряжении комплексного числа, а также об операциях с ними.
- Также изучите их визуализацию на комплексной плоскости и фундаментальную теорему алгебры, теорему Де-Муавра и формулу Эйлера.
- Узнайте о корнях единицы и аргументах комплексных чисел.
- Решите множество задач, связанных с комплексными числами, и научитесь их решать.

Шаг 5. Узнайте о бинарных операциях
Бинарная операция на множестве S - это отображение декартового произведения S на S. Выполнение операции над упорядоченной парой в S дает элемент в S. Таким образом, S называется замкнутым относительно этой операции.
- Операция сложения - это двоичная операция над множеством действительных чисел, потому что сумма любых двух действительных чисел также является действительным числом.
- Множество натуральных чисел не закрывается при вычитании, потому что разность двух натуральных чисел не обязательно является естественной.
- Узнайте об ассоциативности и коммутативности бинарных операций.

Шаг 6. Начните с групп и подгрупп
Определения групп, то, является ли упорядоченная пара (G, *) группой, и различные примеры должны дать вам общее представление о том, как работают группы.
- Изучите различные основные теоремы о группах, такие как теорема, доказывающая существование законов левого и правого сокращения, и теорема, доказывающая единственность тождества и обратного. Также изучите свойства групп и различных специальных групп, таких как группа Zn при сложении по модулю n.
- Узнайте об абелевых группах и их специфических свойствах.
- Исследуйте конечные группы, таблицы Кэли и диаграммы решеток.
- Узнайте о подгруппах, циклических подгруппах, циклических группах, генераторах и их свойствах.
- Также узнайте о полугруппах и моноидах.

Шаг 7. Узнайте об основной идее изоморфизма
Хотя вы можете не полностью понять это на данный момент, важно иметь базовое представление об этом.
- Узнайте об изоморфных и неизоморфных бинарных структурах.
- Изоморфизм исследовательской группы и его последствия.
- Выясните, изоморфны ли некоторые пары групп, например, группа всех действительных чисел относительно сложения изоморфна группе всех положительных действительных чисел при умножении.

Шаг 8. Переход к группам перестановок, орбит и смежных классов, прямым произведениям и конечно порожденным абелевым группам
Изучите определение перестановок, их свойства и умножение перестановок.
- Узнайте о чередующейся группе, четных и нечетных перестановках и теореме Кэли.
- Узнайте об орбитах и циклах, длине цикла, выражении перестановок как продуктов непересекающихся циклов и транспозиций.
- Изучите теорему Лагранжа в смежных классах.
- Изучение прямых произведений, конечно порожденных абелевых групп и фундаментальной теоремы о конечно порожденных абелевых группах.

Шаг 9. Не бойтесь обращаться за помощью
Вы можете спросить своего инструктора или кого-нибудь еще, кто может научить вас. На YouTube есть много видеороликов и много статей в Интернете, посвященных теории групп. Исследуйте и опирайтесь на свои базовые знания.
- Ищите хорошие учебники, стиль которых вам понятен. Решите приведенные в них упражнения.
- Не торопитесь. Разработайте разные задачи и теоремы. Медленно переходите к более продвинутым концепциям теории групп.
