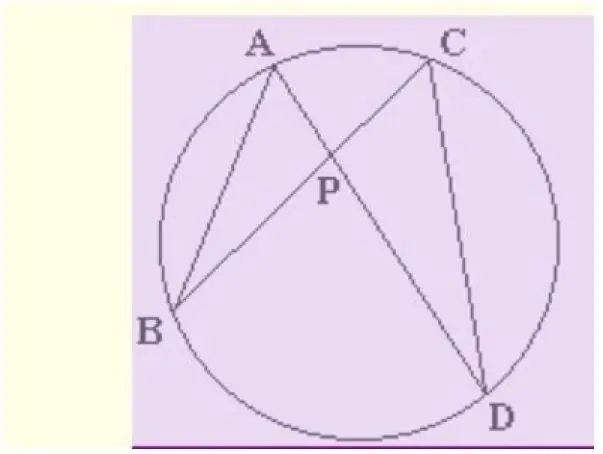
Когда кто-то впервые читает предложение 35 книги III «Элементов» Евклида, можно удивиться тому, что пересекающиеся хорды создают два равных прямоугольника, независимо от того, находится ли их точка пересечения в центре или нет, но это довольно легко понять. Эта статья научит вас доказывать теорему о пересекающихся (или пересекающихся) аккордах; в частности, как две хорды AD и BC создают два равных прямоугольника.
Шаги
Часть 1 из 4: Учебник
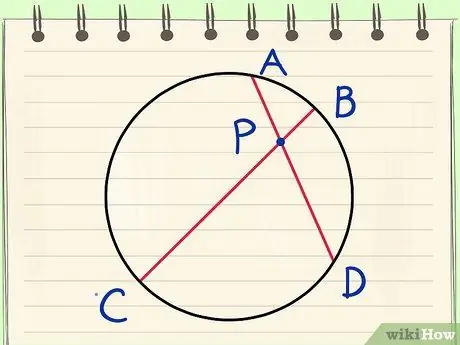
Шаг 1. Понять определение теоремы Евклида о пересекающихся хордах
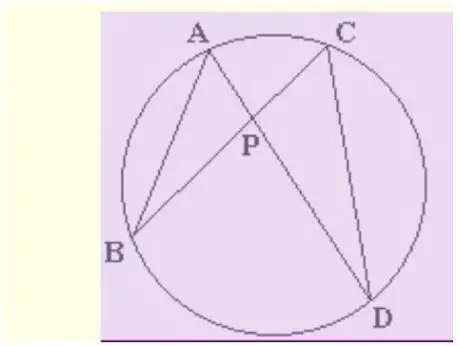
Теорема о пересекающихся хордах утверждает следующий очень полезный факт: дана точка P внутри круга с двумя прямыми, проходящими через P, AD и BC, тогда AP * PD = BP * PC - два прямоугольника, образованные смежными сегментами фактически равны. В этой статье показано, как в несколько шагов доказать, что это правда.
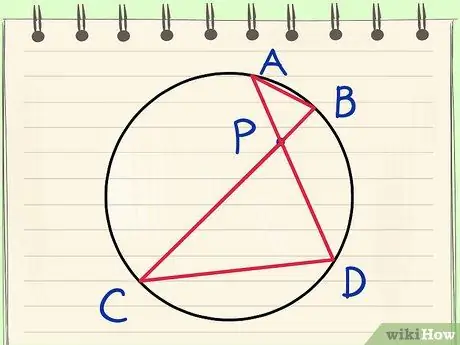
Шаг 2. Докажите сходство треугольников ABP и CDP, которое является следствием их углов, так как:
-
BAD = BCD, потому что вписанные углы, образуемые одной и той же хордой BD, равны [Книга III, предложения 20 и 21];
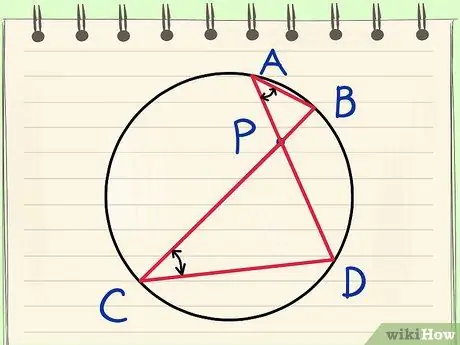
Докажите теорему Евклида о пересекающихся аккордах. Шаг 2 -
ABC = ADC, потому что вписанные углы, образуемые одной и той же хордой AC, равны [Книга III, предложения 20 и 21]; а также
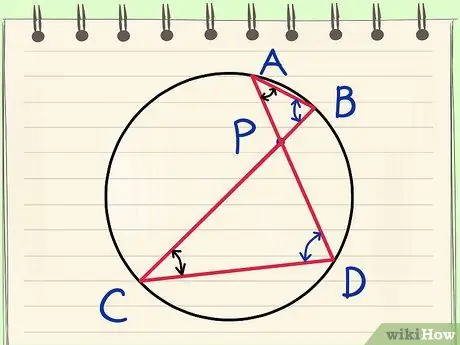
Докажите теорему Евклида о пересекающихся аккордах. Шаг 2. Пункт 2 -
APB = CPD, потому что они представляют собой пару вертикальных углов (вертикальные углы образованы одними и теми же пересекающимися линиями).
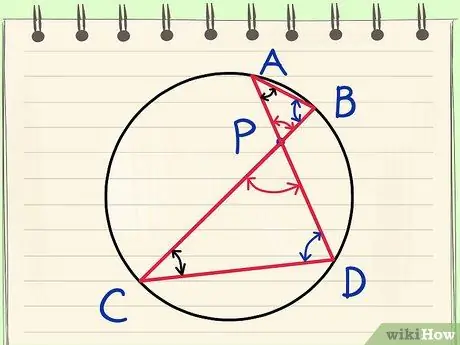
Докажите теорему Евклида о пересекающихся аккордах. Шаг 2. Пункт 3
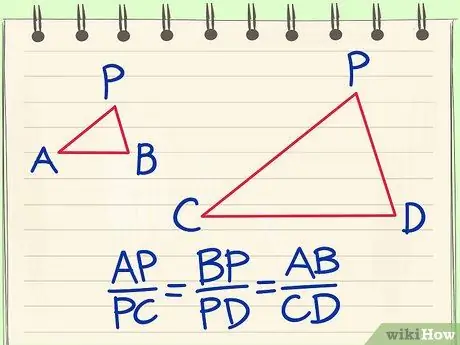
Шаг 3. Докажите, что из подобия треугольников ABP и CDP получаются эти тождества и пропорции:
1) AP / PC = BP / PD = AB / CD. Вот как связаны подобные треугольники.

Шаг 4. Докажите, что первое тождество, приведенное выше, AP / PC = BP / PD, непосредственно приводит к теореме о пересекающихся аккордах путем перекрестного умножения:
AP * PD = BP * ПК. Так была получена теорема, как геометрически, так и математически, поскольку эти два произведения действительно являются прямоугольниками.
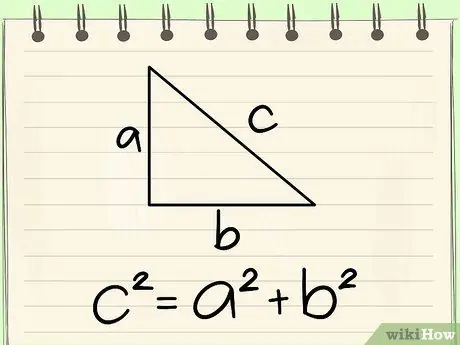
Шаг 5. Изучите и выясните, что доказательство, данное Евклидом, намного длиннее и сложнее и использует теорему Пифагора, которая сама по себе является довольно длинным доказательством
Чтобы понять, как работают эти доказательства, обратитесь к переведенному тексту «Элементов» Евклида ниже.
Часть 2 из 4: пояснительные таблицы, диаграммы, фотографии
Часть 3 из 4: Полезное руководство
Шаг 1. Используйте вспомогательные статьи при выполнении этого руководства:
- См. Статью «Как размножать и делить геометрически, как мать-природа», где приведен список статей, связанных с Excel, геометрическим и / или тригонометрическим искусством, построением диаграмм / диаграмм и алгебраическими формулировками.
- Для получения дополнительных графиков и диаграмм вы также можете щелкнуть Категория: Изображения Microsoft Excel, Категория: Математика, Категория: Таблицы или Категория: Графика, чтобы просмотреть множество листов и диаграмм Excel, в которых тригонометрия, геометрия и исчисление были превращены в искусство, или просто щелкните категорию, отображаемую в правой верхней белой части этой страницы или в левом нижнем углу страницы.
Часть 4 из 4: Видеопомощь. Используя эту услугу, некоторая информация может быть передана YouTube
подсказки
-
Доказательство Евклида зависит от его доказательства теоремы Пифагора; вот изображение этого доказательства:
- Чтобы помочь понять, как углы с равными основаниями в круге имеют одинаковый угол на их дальних концах, где они снова касаются круга, здесь воспроизведены два изображения предыдущих теорем Евклида, предложения 20 и 21 КНИГИ III:
-
Выше было сказано, что собственное доказательство Евклида, Книга III P35, было намного длиннее и сложнее, поскольку оно также включает доказательство теоремы Пифагора. Вот изображение доказательства: