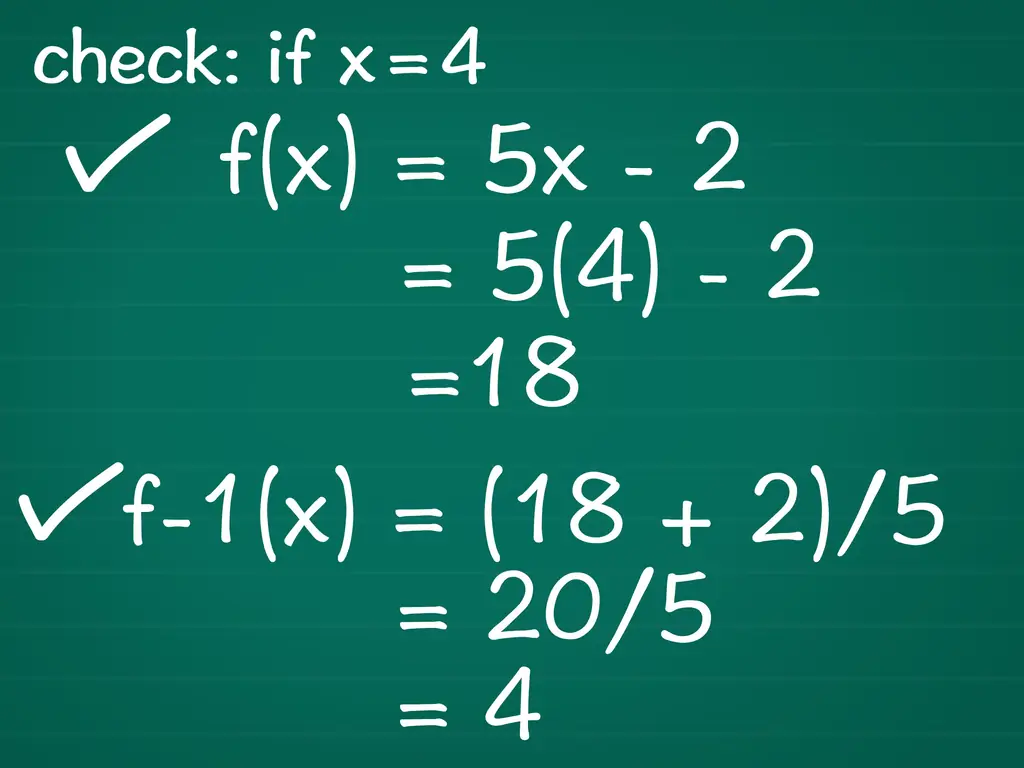Математическую функцию (обычно обозначаемую как f (x)) можно рассматривать как формулу, которая даст вам значение для y, если вы укажете значение для x. Функция, обратная функции f (x) (которая записывается как f-1(x)) по сути является обратным: введите значение y, и вы получите исходное значение x обратно. Поиск функции, обратной функции, может показаться сложным процессом, но для простых уравнений все, что требуется, - это знание основных алгебраических операций. Читайте пошаговые инструкции и иллюстративный пример.
Шаги
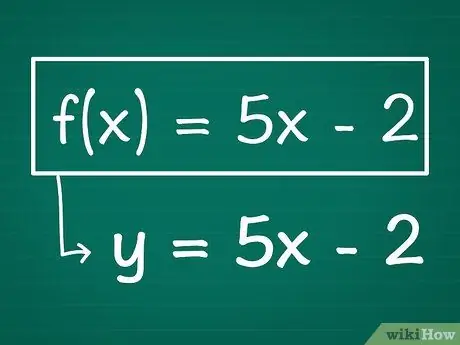
Шаг 1. Напишите вашу функцию, при необходимости заменив f (x) на y
Ваша формула должна содержать y с одной стороны от знака равенства, а члены x - с другой стороны от знака равенства. Если у вас есть уравнение, которое уже записано в терминах y и x (например, 2 + y = 3x2), все, что вам нужно сделать, это решить для y, выделив его по одну сторону от знака равенства.
- Пример: если у нас есть функция f (x) = 5x - 2, мы бы переписали ее как у = 5х - 2 просто заменив "f (x)" на y.
- Примечание: f (x) - это стандартная запись функций, но если вы имеете дело с несколькими функциями, каждая из них получает разные буквы, чтобы их было легче различать. Например, g (x) и h (x) являются общими идентификаторами для функций.
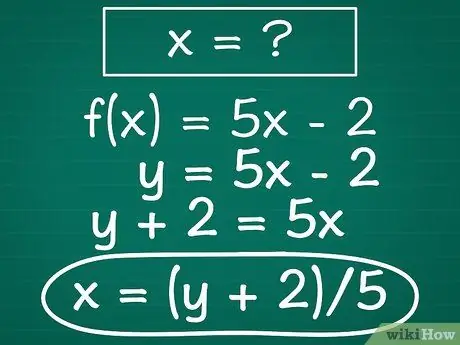
Шаг 2. Решите относительно x
Другими словами, выполните необходимые математические операции, чтобы изолировать x по одну сторону от знака равенства. Здесь вас подскажут основные алгебраические принципы: если x имеет числовой коэффициент, разделите обе части уравнения на это число; если к члену x с одной стороны от знака равенства добавлено определенное число, вычтите это число с обеих сторон и т. д.
- Помните, что вы можете выполнять любую операцию с одной стороной уравнения, если вы выполняете операцию с каждым членом по обе стороны от знака равенства.
- Пример: чтобы продолжить наш пример, сначала мы добавим 2 к обеим сторонам уравнения. Это дает нам y + 2 = 5x. Затем мы разделим обе части уравнения на 5, получив (y + 2) / 5 = x. Наконец, чтобы облегчить чтение, мы перепишем уравнение с «x» слева: х = (у + 2) / 5.
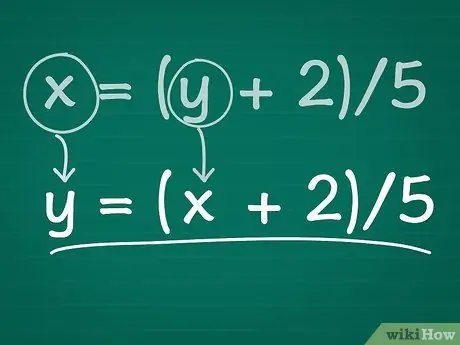
Шаг 3. Переключите переменные
Замените x на y и наоборот. Полученное уравнение является обратным по отношению к исходной функции. Другими словами, если мы подставим значение для x в наше исходное уравнение и получим ответ, когда мы подставим этот ответ в обратное уравнение (снова для x), мы вернем исходное значение!
Пример: после переключения x и y у нас будет у = (х + 2) / 5
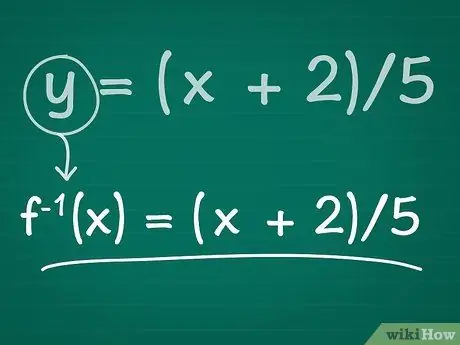
Шаг 4. Замените y на f-1(Икс).
Обратные функции обычно записываются как f-1(x) = (x терминов). Обратите внимание, что в этом случае показатель -1 не означает, что мы должны выполнить операцию экспоненты для нашей функции. Это просто способ указать, что эта функция является обратной по отношению к нашему оригиналу.
Поскольку преобразование x в -1-ю степень дает дробь 1 / x, вы также можете думать о f-1(x) как способ записи «1 / f (x)», что также означает обратное к f (x).
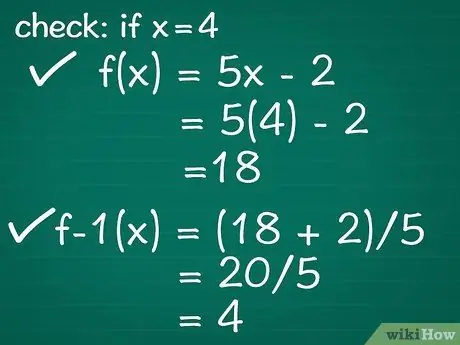
Шаг 5. Проверьте свою работу
Попробуйте подставить константу в исходную функцию вместо x. Если вы нашли правильную обратную функцию, вы сможете вставить результат в обратную функцию и получить исходное значение x в качестве результата.
- Пример: заменим 4 на x в нашем исходном уравнении. Это дает нам f (x) = 5 (4) - 2 или f (x) = 18.
- Затем давайте подставим наш ответ 18 в нашу обратную функцию для x. Если мы сделаем это, мы получим y = (18 + 2) / 5, что упрощается до y = 20/5, что дополнительно упрощается до y = 4. 4 - это наше исходное значение x, поэтому мы знаем, что вычислили правильная обратная функция.
подсказки
- Вы можете свободно заменять f (x) = y и f ^ (- 1) (x) = y назад и вперед, когда выполняете алгебраические операции над своими функциями. Но сохранение исходной функции и обратной функции прямо может запутать, поэтому, если вы не работаете активно ни с одной из функций, попробуйте придерживаться обозначения f (x) или f ^ (- 1) (x), что поможет вам Расскажите им обособленно.
- Обратите внимание, что обратная функция функции обычно, но не всегда, является самой функцией.