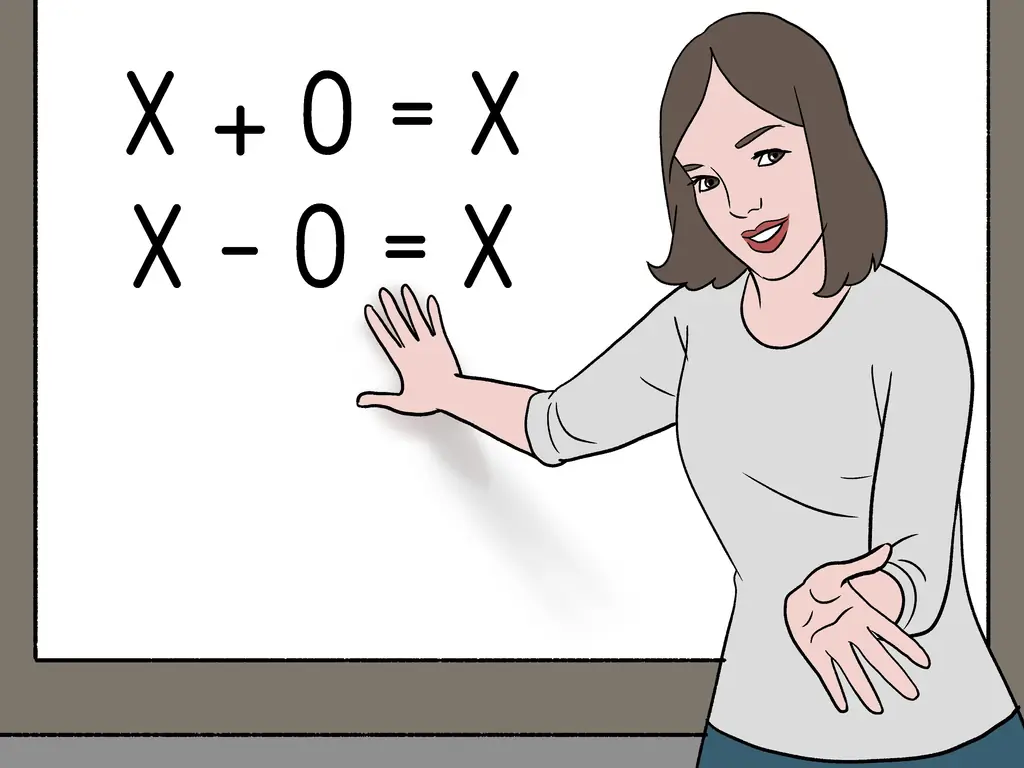Ноль - это особенное и уникальное число, и некоторые люди не знают, как его использовать. Число ноль - это символ, используемый для обозначения отсутствия чего-либо. Это базовое руководство по свойствам нуля и его использованию в повседневной математике.
Шаги
Метод 1 из 6: понимание концепции нуля

Шаг 1. Знайте, что ноль - это абсолютно ничего
Из-за этого он не такой, как другие числа. Если вы скажете кому-то, что осталось ноль кусочков пирога, это то же самое, что сказать, что пирога больше нет. Вы не можете считать ноль или взять его долю.
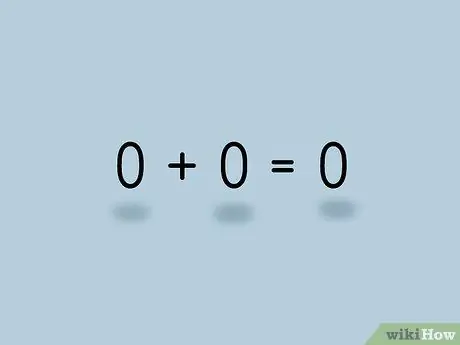
Шаг 2. Знайте, что ноль не является ни отрицательным, ни положительным
Это потому, что положительные и отрицательные числа определены относительно нуля. Положительные числа больше нуля, а отрицательные числа меньше нуля. Ноль не может быть больше или меньше самого себя, поэтому нет таких понятий, как +0 или -0. Противоположность нулю равна нулю, поскольку 0 + 0 = 0.
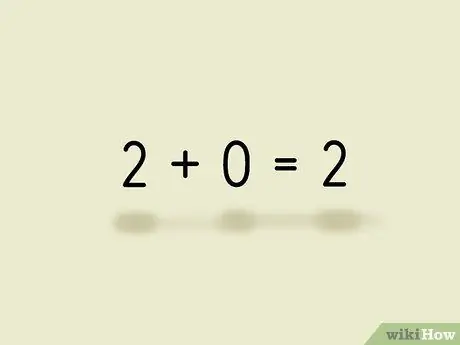
Шаг 3. Поймите, что ноль - четное число
Это можно доказать разными способами:
- Четное число плюс четное число дает четное число. 2 + 0 = 2. Следовательно, ноль должен быть четным числом.
- Четное число, разделенное на два, дает ноль в качестве остатка. Поскольку ноль, деленный на два, равен нулю, с нулем в качестве остатка, ноль должен быть четным числом.
- Фактически, ноль, возможно, является самым четным числом. Шесть является единственно четным, потому что вы можете разделить его на два, один раз, а двенадцать - вдвойне, потому что вы можете разделить его на два, а затем снова на два. Так что в некотором смысле двенадцать больше, чем шесть. Поскольку вы можете продолжать делить ноль на два до бесконечности, это самое четное число.
Метод 2 из 6: добавление нуля
Шаг 1. Знать тождественное свойство сложения
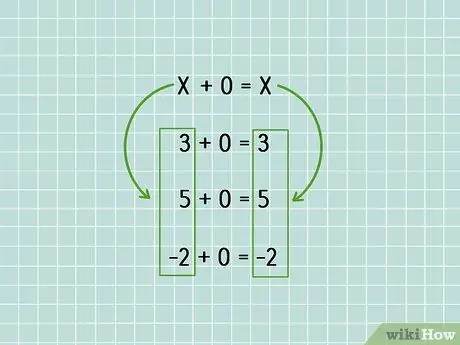
Это означает, что когда вы добавляете 0 к числу, вы получаете исходное число обратно; в форме уравнения это будет x + 0 = x.
- 3 + 0 = 3
- 5 + 0 = 5
- -2 + 0 = -2
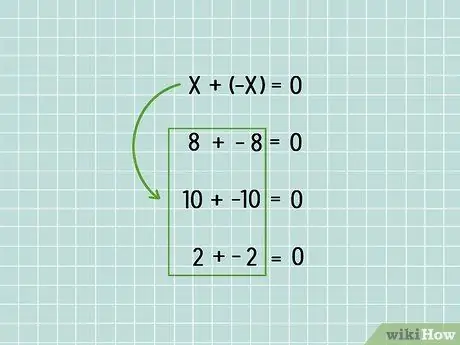
Шаг 2. Поймите, что когда вы складываете число и его противоположность, в сумме получается 0
В форме уравнения это будет x + (-x) = 0. Противоположность числа называется его аддитивной инверсией, а сумма двух аддитивных инверсий всегда равна нулю.
- -8 + 8 = 0
- 10 + -10 = 0
- -2 + 2 = 0
Метод 3 из 6: использование нуля при вычитании

Шаг 1. Вычтите 0 из числа
Когда вы это сделаете, вы получите тот же номер обратно. Это означало бы:
- 2 - 0 = 2
- 5 - 0 = 5
- -16 - 0 = -16

Шаг 2. Вычтите число из 0
0 минус любое число - это противоположность этого числа или его аддитивная инверсия. В форме уравнения это будет 0 - x = (-x) или 0 - (-x) = x.
- 0 - 1 = (-1)
- 0 - 2 = (-2)
- 0 - (-180) = 180
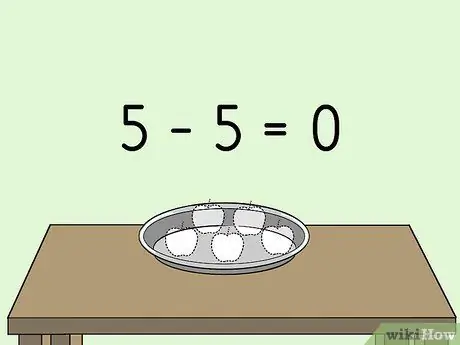
Шаг 3. Вычтите число из самого себя
Это все равно, что положить на стол пять яблок и убрать все пять. Если вы это сделаете, вы получите ноль. То же самое относится к вычитанию отрицательного числа из самого себя; когда вы это сделаете, вы также получите ноль.
- 2 - 2 = 0
- 5 - 5 = 0
- -12 - (-12) = 0
Метод 4 из 6: использование нуля при умножении и делении
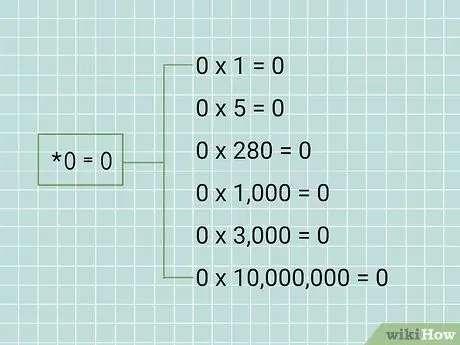
Шаг 1. Знать мультипликативное свойство нуля
Это означает, что когда вы умножаете любое число на ноль, произведение всегда будет равно нулю, независимо от того, насколько велико число. В форме уравнения это будет * 0 = 0.
- 0 х 1 = 0
- 0 х 5 = 0
- 0 х 280 = 0
- 0 х 1 000 = 0
- 0 х 3 000 = 0
- 0 х 10 000, 000 = 0
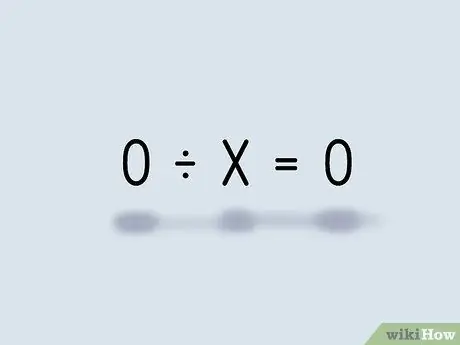
Шаг 2. Разделите 0 на число
Когда у вас 0 в дивиденде задачи деления, вы всегда получите ноль.

Шаг 3. Знайте, что делить на 0 нельзя
Выражение, в котором ненулевое число делится на ноль, не определено. Например, 28/0 - это то же самое, что спросить: "какое число, умноженное на 0, равно 28?" Такого числа нет, так как все, умноженное на 0, равно 0.
0/0 - частный случай этого правила. Его можно переформулировать как «какое число раз 0 равно нулю?» Или «0x = 0». Поскольку x может быть любым числом, это выражение неопределенно
Метод 5 из 6. Использование нуля в экспонентах
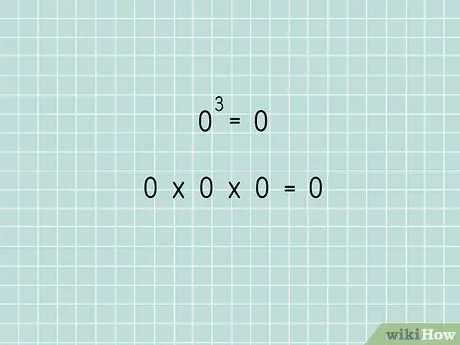
Шаг 1. Знайте, что ноль в любой степени по-прежнему равен нулю
Это было бы как 0 x 0 x 0 x 0 или ничего не умножить ни на что несколько раз. Поскольку умножение на ничто никогда никуда не приведет, 0 для любой степени остается 0 навсегда.
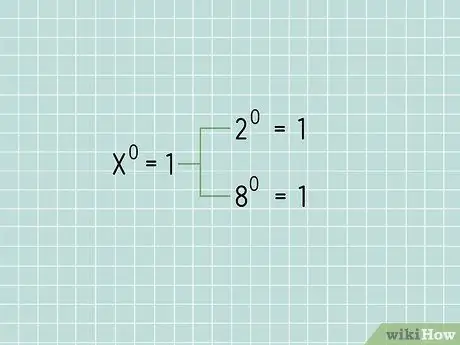
Шаг 2. Знайте, что любое ненулевое число в степени 0 равно 1
Например, 2 в степени 0 равно 1, а 8 в степени 0 равно 1.
0 в степени 0 является неопределенным, так как «незаконно» деление на ноль, и, таким образом, деление 0 на себя является неопределенным
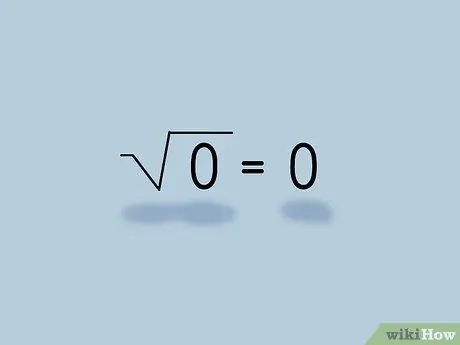
Шаг 3. Поймите, что квадратный корень из нуля равен нулю
Извлечение квадратного корня из нуля можно переформулировать как «сколько раз само число равно нулю». 0 * 0 = 0, поэтому квадратный корень из нуля равен нулю.
Это верно для любого корня из нуля: nth корень из нуля равен нулю, пока n не равно нулю.
Метод 6 из 6: обучение учеников начальной школы нулевому значению

Шаг 1. Покажите им, что ноль - это ничто
Назовите предмет, которого у вас нет, и скажите своим ученикам, что если вы попытаетесь его сосчитать, у вас ничего не получится. Во-первых, нечего считать.

Шаг 2. Научите их использовать ноль в качестве заполнителя (см. Раздел «Советы»)
Шаг 3. Скажите им, что прибавлять или вычитать ноль бесполезно
У вас будет такая же ценность; это совершенно бессмысленно.